致密油藏分段多簇压裂水平井复杂缝网表征及产能分析

徐加祥 ，丁云宏 ，杨立峰 ，高 睿 ，刘 哲 ，王 臻

（1.中国石油勘探开发研究院，北京100083；2.中国石油勘探开发研究院压裂酸化技术服务中心，河北廊坊065007；3.中国石油油气藏改造重点实验室，河北廊坊065007）

随着中国各大油田普遍进入开发中后期，致密油等非常规资源成为油气上产的主力［1］，然而致密油储层的孔渗条件较差且天然裂缝发育，常规水力压裂方式难以实现经济有效的开发［2-4］。新疆、长庆等油田经过多年的矿场实践证明，体积压裂是开发该类油藏的有效手段［5-7］，对水平井分段压裂后致密油储层产能的评价是制定合理压裂和采油参数的基础。中外众多学者在该领域做了大量工作，在研究稳态和非稳态产能的过程中，分别对不同形态水力裂缝参数（裂缝条数、裂缝导流能力、裂缝角度）和基质物性（渗透率各向异性）的敏感性进行了分析［8-10］，并考虑储层应力敏感性［11-13］以及多裂缝之间互相干扰的影响［14］。对于裂缝性油藏天然裂缝的处理，部分学者在油藏中划定平行的裂缝网络或采用分形理论形成树状网络，进而对基质和裂缝中的渗流过程分别进行研究［15-16］；还有学者采用连续介质渗透率张量模型，利用各向异性渗透率的二阶张量，对裂缝和基质的渗透率进行等效分析［17-18］。但以上研究均无法准确地反映天然裂缝在储层中的真实分布状况以及对水平井产能的影响。

基于上述问题，以S油田某油井的实测裂缝数据为参考，利用COMSOL和MATLAB软件联合仿真技术对储层中的实际裂缝形态进行建模，通过基质-裂缝-井筒耦合流动模型对压裂后致密油藏产能进行模拟，并分析不同水力裂缝长度和间距对产能的影响。研究成果对致密油藏复杂缝网建模及产能模拟具有一定的指导意义。

1 致密油藏复杂缝网建模

为了使所构建的压裂后致密油藏的缝网结构更符合真实地质情况，有必要对压裂后油藏的组成部分进行分析并分别建模。对于天然裂缝发育的致密油储层，在水平井分段压裂之后，储层中流体的渗流通道主要包括以下4个部分：①岩石基质。该部分是致密油藏中油气的主要存储和流动空间，其物性条件在一定程度上决定压裂井的单井控制范围。②天然裂缝。天然裂缝的形成受构造作用影响，其分布密度和走向并非均匀随机，而是呈现一定的规律性。③水力裂缝。在压裂过程中压裂液在油藏中造缝，同时受天然裂缝影响，会在主裂缝两侧形成次级裂缝，其与天然裂缝相互交错延伸形成缝网，且这些次级裂缝的走向往往受地层主应力变化的影响。④水平井井筒。水平井井筒的长度和位置由具体施工参数决定。

对于致密油藏的岩石基质和天然裂缝，以S油田某油井的实测数据为例进行分析。S油田发育源储一体油藏，其孔隙度为11%，基质渗透率为0.012 mD。储层具有较好的岩石脆性，最大和最小水平主应力的差异较小，天然裂缝较为发育（表1）；其中S-4井最大天然裂缝密度为8.65条/m，但平均天然裂缝密度仅为2.87条/m，可见其天然裂缝分布并不均匀。由于无法确定天然裂缝的具体分布位置，拟采用天然裂缝密度分布较为均匀的S-2井进行建模，其最大天然裂缝密度为1.12条/m，平均天然裂缝密度为0.71条/m，二者差距较小，因此可认为该井的天然裂缝分布较为均匀，取其平均天然裂缝密度进行建模。

表1 S油田致密油藏天然裂缝密度分布Table1 Natural fracture density in tight oil reservoir of S Oilfield

此外，致密油藏天然裂缝的走向并不是随机分布的，且直接影响压裂后裂缝缝网的形成。S-2井天然裂缝走向分布如表2所示。天然裂缝按照导流能力不同分为高导缝和高阻缝，S-2井高导缝走向主要为N0°E—N10°E以及N20°E—N40°E，高阻缝走向主要为N30°E—N40°E，在建模过程中排除高阻缝的影响，仅对高导缝进行模拟，且天然裂缝长度为40～60 m。

表2 S油田S-2井天然裂缝走向分布Table2 Natural fracture strike of Well S-2 of S Oilfield

水力裂缝参数对压裂井产能的影响是本次研究的重点，主裂缝长度分别取80，120和160 m，裂缝间距分别取10，15和20 m。次级裂缝由于受主应力影响，与主裂缝呈锐角分布，其方位角在N45°E—N45°W随机分布，裂缝密度为0.5条/m，裂缝长度为15～30 m。水平井井筒沿X方向，长度为1 500 m。

研究中不考虑裂缝的迂曲状况，将其视为直线段处理。利用COMSOL和MATLAB软件联合仿真技术，可以在天然裂缝分布认识不清且仅有上述部分统计数据的条件下，实现所需裂缝形态的几何建模，尽可能地接近矿场实际。在该过程中，利用程序中参数化曲线的parmax，rot和pos等关键词可以分别控制裂缝的长度、走向和位置，并利用达西定律模块以及管流模块建立流体在基质、裂缝和井筒中流动的数学模型进行求解。

2 裂缝-基质-井筒耦合流动模型的建立及验证

对于流体在油藏基质中的流动可以利用达西方程［19］表示：

其中：

为了模拟流体在裂缝中的流动，对达西方程的系数进行修改以符合其高导流能力特点，并实现基质与裂缝之间流速和压力分布的连续性，其表达式为：

流体在水平井井筒中的流动可以用Navier-Stokes方程［20］表示：

根据S-2井的油藏基质物性和裂缝参数对该井的复杂缝网进行建模，对S-2井流体在基质、裂缝及井筒内的流动过程进行分析。S-2井实测日产油量及数值模拟结果（图1）表明，其模拟日产油量与实测数据的变化趋势基本一致，验证了所建模型的准确性和可靠性。

3 模拟结果分析

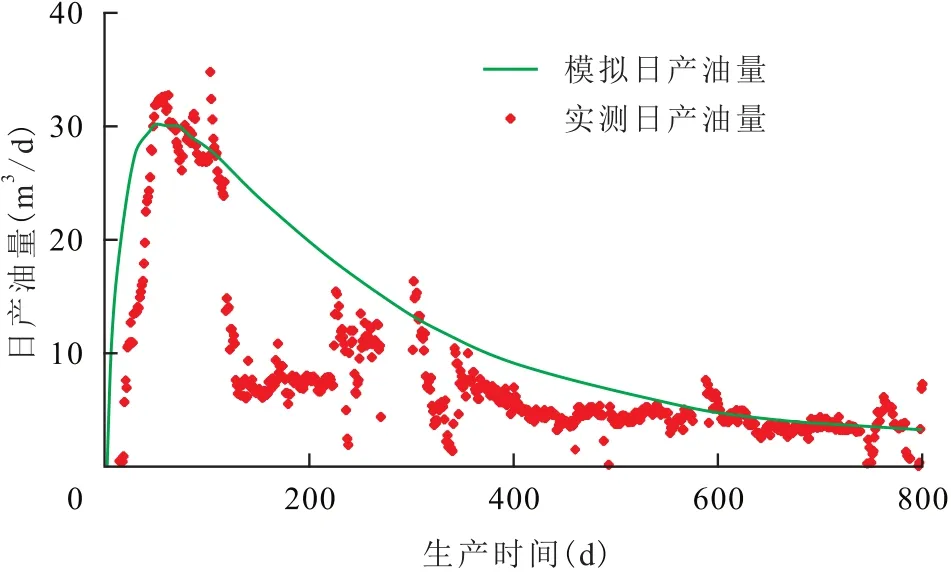
图1 S-2井模拟和实测日产油量Fig.1 Simulated and actual daily oil production of Well S-2

COMSOL是一款利用有限元方法求解偏微分方程（组），从而进行多物理场耦合计算的数值模拟软件，其内置的数学模型灵活，材料属性设置方便，并内置MATLAB接口进行复杂逻辑处理。利用该软件对致密油藏中流体在基质、裂缝及井筒内的耦合流动过程进行分析，油藏边界设置为定压边界，且定压生产，其他模拟参数包括：油藏宽度为600 m、长度为1 600 m，边界压力为30 MPa，生产压力为15 MPa，原油密度为880 kg/m3，地面原油黏度为45 mPa·s，水力裂缝导流能力为30 μm2·cm，天然裂缝导流能力为10 μm2·cm。

3.1 不同生产时间下的压力分布特征

为了便于观察致密油藏压裂后开发压力在井筒、水力裂缝及天然裂缝中的分布情况并减少计算量，以1 260～1 500 m井段的10条水力裂缝及周围的天然裂缝为例进行说明。由于井筒在1 260 m处的压力并不是生产压力，需模拟井筒压力变化过程，以获得1 260 m处准确的井筒压力，确保模拟部分的压力变化特征与油藏整体压力变化一致。

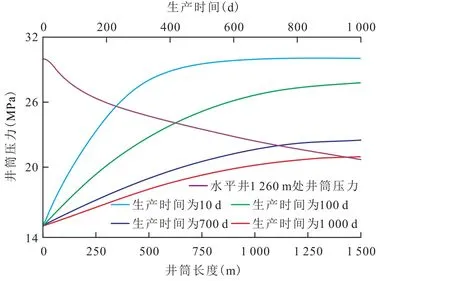
图2 水平井的井筒压力随生产时间的变化特征Fig.2 Pressure variation of horizontal wellbore

由水平井井筒压力随生产时间的变化特征（图2）可见，流体压力由水平井的井筒端部不断波及到井筒内部。在生产初期，整个井筒压力变化较大，不能简单地认为井筒中为单一压力。图2中的下降曲线反映水平井1 260 m处的井筒压力随生产时间的变化特征，该处井筒压力由30 MPa降至约为21 MPa，呈现降速变缓的压力下降过程。将1 260 m处的井筒压力设置为边界条件，进行后续的油藏压力分布模拟。

图3 致密油藏复杂缝网在不同生产时间下压力分布特征Fig.3 Pressure distribution of complex fracture network in tight oil reservoir at different production time

通过数值模拟，得到致密油藏复杂缝网在生产时间分别为100，300，600和1 000 d的压力分布情况（图3）。结果表明，在油藏开发初期，由于井筒和主裂缝区域的导流能力较强，使得该区域可以迅速被波及。随着生产时间推移，油藏中低压区域的波及范围由主裂缝和部分次级裂缝向两侧基质呈现不规则扩展，沟通天然裂缝并影响相应的基质区域，表现出较强的非均质性。缝网中裂缝密度越大的区域，其压力波及效果越显著；未压裂区域由于裂缝之间的连通性较差，压力波及程度也较差，但在改造区域外围与水力主裂缝或次级裂缝连通的天然裂缝可以在一定程度上增大压力波及范围。在整个致密油藏范围内，压力低于25 MPa的区域面积占整个油藏面积的比例在生产初期迅速增加并逐渐稳定；当生产时间为1 000 d时，压力波及区域的面积约占整个油藏面积的34.1%。

3.2 不同水力裂缝长度下的产能变化特征

图4 不同水力裂缝长度下致密油藏压裂产能变化特征Fig.4 Productivity of fractured tight oil reservoir with different length of hydraulic fractures

在实际矿场施工过程中，可控的裂缝参数为裂缝长度和裂缝间距。取裂缝间距为15 m，分别对水力裂缝长度为80，120和160 m条件下致密油藏压裂后的产能变化特征进行分析。结果（图4）表明，就某一裂缝长度而言，在生产初期，油井日产油量均在短时间内呈大幅上升的趋势，这是由于生产初期主要是导流能力强的主裂缝及周围区域的油气向井筒内汇流（图4a）。同时日产油量随着水力裂缝长度的增加而升高，水力裂缝长度分别为80，120和160 m所对应的初始日产油量分别为42.5，45.8和50.1 m3/d，但是增加幅度逐渐减小。随着生产时间的推移，日产油量迅速下降，1 000 d的日产油量均降至约为3 m3/d，无法实现较长时间的稳产。此外，油井累积产油量在生产初期迅速增加（图4b），在日产油量下降后，逐渐进入稳定阶段。当生产时间为1 000 d时，3种水力裂缝长度下的累积产油量分别为6 163，7 912和8 362 m3，累积产油量随水力裂缝长度增大而增加的幅度明显变缓，继续增加裂缝长度对增加累积产油量的意义不大，因此最佳的水力裂缝长度约为160 m。

3.3 不同水力裂缝间距下的产能变化特征

在水力裂缝间距分别为10，15和20 m的条件下，对致密油藏压裂后的日产油量和累积产油量进行模拟，模拟过程中固定水力裂缝长度均为160 m，水力裂缝间距增加幅度与水力裂缝长度的增加幅度相同，使结果更具对比性。与增加水力裂缝长度相比，减小裂缝间距可以在生产初期获得更高的日产油量且增产效果较明显（图5a）。这是由于较小的裂缝间距可以形成更密集的裂缝网络，使得油藏动用程度更高，压力传播所经过的距离更短，油井累积产油量也得到提高。在水力裂缝间距为10 m的条件下，生产时间为1 000 d的累积产油量为10 453 m3；在水力裂缝间距为20 m的条件下，生产时间约为200 d的日产油量即衰减至初始日产油量的10%左右；在水力裂缝间距缩小至15 m的条件下，生产时间约为600 d的日产油量即衰减至初始日产油量的10%左右（图5b）。与延长水力裂缝长度类似，减小水力裂缝间距所获得的产油量增量不断减少，继续缩短水力裂缝间距对增加累积产油量的意义不大。通过模型模拟得到较为适宜的裂缝间距约为10 m。

4 结论

利用COMSOL和MATLAB软件联合仿真技术提出在天然裂缝认识较为局限的条件下，以地质资料为依据对天然裂缝、水力主裂缝及次级裂缝进行建模的方法，并利用该软件分别对基质、裂缝和井筒中的流动过程进行模拟，为压裂后致密油藏产能分析提供更为合理的理论依据。

在致密油藏复杂缝网中，压力由井筒和主裂缝依次波及至次级裂缝、天然裂缝和基质，改造区域周边的裂缝对增大压力波及范围具有一定作用。增加水力裂缝长度和减小水力裂缝间距均可以提高油井的日产油量和累积产油量。在考虑裂缝及井筒有限导流能力的条件下，数值模拟得到的最优水力裂缝长度和裂缝间距分别为160和10 m。在变化幅度相同的条件下，缩小水力裂缝间距比延长水力裂缝长度对提高油井产油量更为有利。

符号解释

ρ——地层流体密度，kg/m3；S——基质存储系数，1/MPa；p——流体压力，MPa；t——生产时间，d；K——基质渗透率，mD；μ ——地层流体黏度，mPa·s；Gl——流体压缩系数，1/MPa；ϕ ——孔隙度，f；Gs——基质压缩系数，1/MPa；Sf——裂缝存储系数，1/MPa；df——裂缝宽度，mm；Kf——裂缝渗透率，mD；u——流体流速，m/s；g——重力加速度，m/s2。