非均质水驱油藏无因次采液指数曲线的预测及应用

肖 武

（中国石化胜利油田分公司勘探开发研究院，山东东营257015）

近年来，胜利油区各大主力油田均已进入高含水至特高含水期，剩余油分布及剩余可采储量动用潜力持续成为研究热点和开发调整的重点，理论研究和大量矿场实践表明，储层非均质性及油水黏度差异降低了储层内的水驱波及程度，导致油井提前见水、无效水循环和见水后产量快速递减。保持合理采液量规模是延缓水驱油藏中高含水期产量递减的一项重要措施［1-6］，措施有效的前提条件是当前采出程度较低，且储层具有较大的提液潜力［7-9］。水驱波及系数可表征油藏的非均质程度及注采井网的完善程度，采液能力则可通过无因次采液指数随含水率的变化趋势来预测。前人对基于油水相对渗透率的无因次采液指数计算方法进行了大量的研究和改进［10-12］，但鉴于研究尺度和数据来源的局限性，始终未能考虑由于储层非均质性导致的地层中油水分布及其变化过程对采液能力的影响。为此，笔者以模拟非均质油藏的经典并联岩心水驱油实验数据为基础，回归建立了渗透率及渗透率级差对无因次采液指数随含水率变化规律影响程度的多元方程及指标曲线图版；进一步将实际非均质油藏划分为水驱波及区和未波及区，将岩心测试的相对渗透率数据仅应用于波及区，计算不同波及系数时的油藏无因次采液指数图版；最后通过测算水驱波及系数进而得到非均质油藏无因次采液指数的变化规律，还可根据矿场实测采液指数推算水驱波及系数，为剩余油挖潜提供理论依据。

1 非均质油藏无因次采液指数影响因素实验

1.1 并联岩心驱替实验原理

常规单岩心水驱油实验反映了微观非均质性对油水相对流动能力的影响，即使是取自同一层段的岩心，由于存在显著的微观非均质性，所测得的有效渗透率及相对渗透率曲线形态也会有较大差异。为了体现实际油藏大尺度条件下的层间及平面渗透率差异，采用并联岩心驱替实验流程，在岩心间设置较大渗透率差异，测试数据能够体现渗透率级差对地层油水相对流动能力的影响，进而可计算无因次采液指数曲线，分析非均质性对水驱油藏高含水期油井采液能力的影响。

1.2 无因次采液指数主控因素的对比实验方案

采用具有不同粒径组合的石英砂和不同含量的黏土，在模具里制作了不同长度、不同渗透率的人造岩心，在恒压条件下分别进行单岩心、双岩心并联及三岩心并联的非稳态水驱油实验。人造岩心的长度分别为5，20和100 cm，气测渗透率从595 mD到5 234 mD，并联岩心渗透率级差最大为8.7，驱替压力梯度为0.05～0.4 MPa/m，配制油平均黏度为15 mPa·s。

记录油、水流出量和对应的时间，计算无因次采液指数，绘制无因次采液指数随含水率的变化曲线。

1.3 建立非均质储层无因次采液指数曲线的经验公式

从实验数据的变化趋势可以看出，无因次采液指数随含水率的变化规律符合一元三次方程，且截距为1，对实验数据进行回归，可得方程式为：

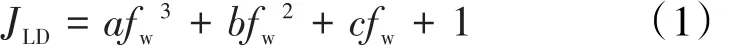
针对每组实验数据，无因次采液指数曲线方程的系数如表1。

对比具有相近渗透率级差的无因次采液指数曲线方程中的系数a，b，c，发现三者均与渗透率呈线性关系，即：

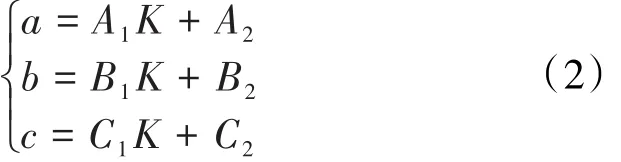
将表1中数据分别代入（2）式，回归得到无因次采液指数曲线方程系数a，b，c关于渗透率的线性方程系数（表2）。

研究分析发现，表2中各个系数关于渗透率级差呈现出线性或指数变化规律，从而表明无因次采液指数也是关于渗透率级差的函数。

回归方程式分别为：

综上所述，基于岩心测试数据建立的多因素无因次采液指数曲线的经验公式为：

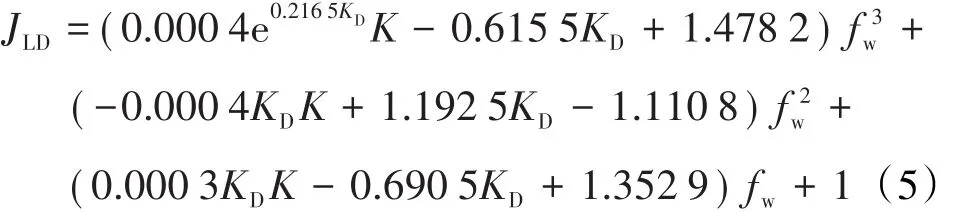
1.4 绘制无因次采液指数的校正图版

本文所建立的无因次采液指数曲线方程的系数均来自岩心实验，反映的是实验岩样在完全被水驱波及条件下的油水相对流动能力。实际油藏的非均质性越强，则水驱波及程度越差，高含水期的采液能力将随油藏非均质性的增强而降低。

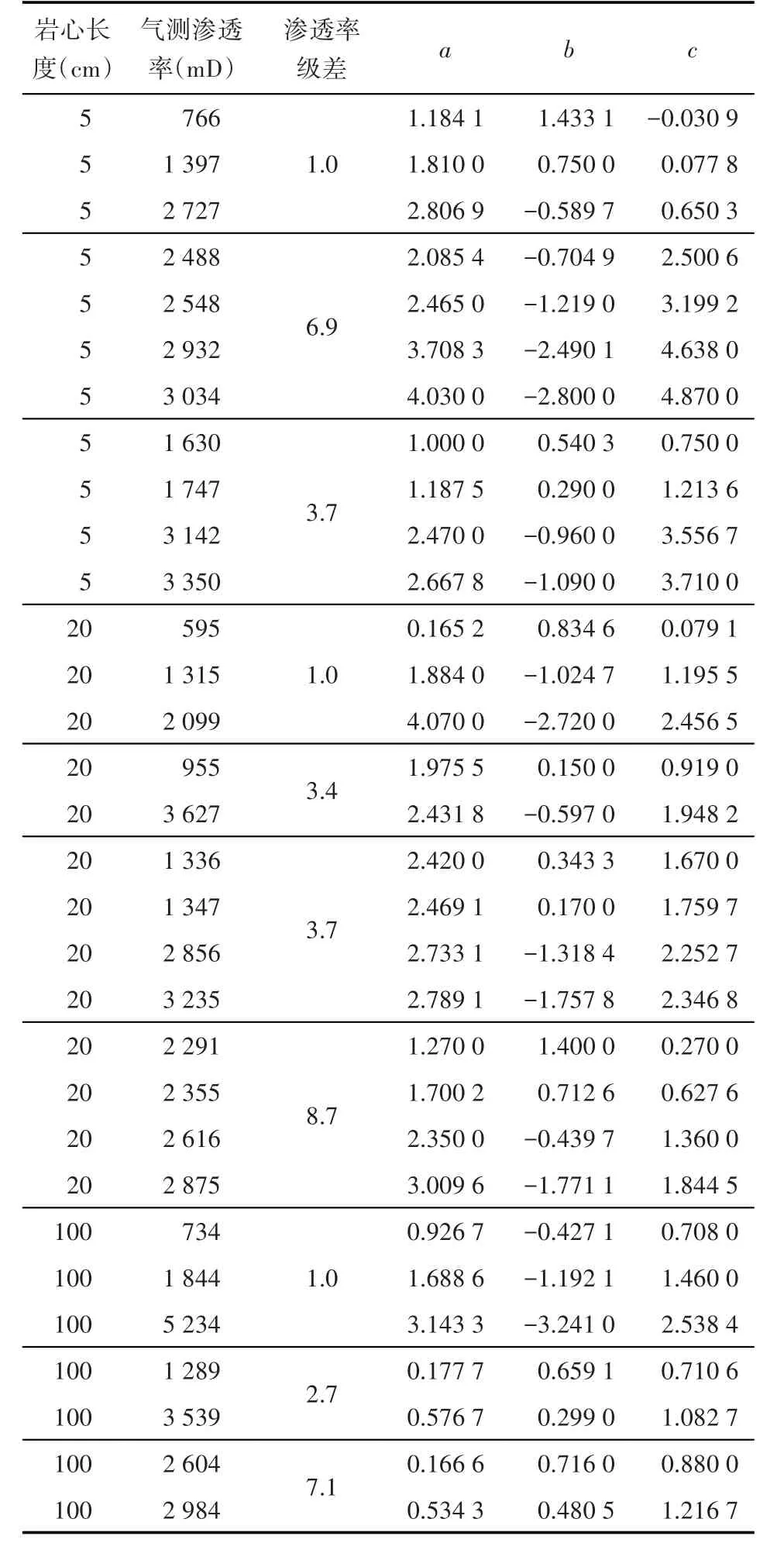
表1 基于并联岩心驱替实验数据建立的无因次采液指数曲线方程系数Table1 Coefficients of dimensionless liquid production index curve equation based on parallel core displacement experimental data

为了突出物性及其非均质性对采液能力的影响，并削弱实验岩样之间油水相对流动能力差异的干扰，以具有最低渗透率实验岩样的无因次采液指数曲线为基准，绘制不同渗透率及渗透率级差下无因次采液指数增幅随含水率变化规律的校正图版（图1）。

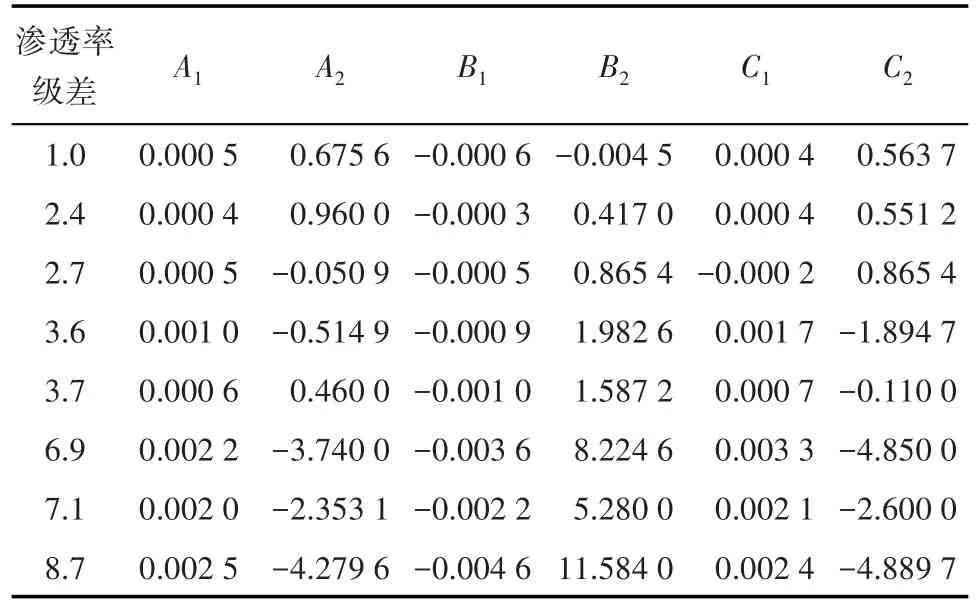
表2 无因次采液指数曲线方程系数关于渗透率的线性方程系数Table2 Linear equation coefficients of coefficient items of non-dimensional liquid production index curve on permeability

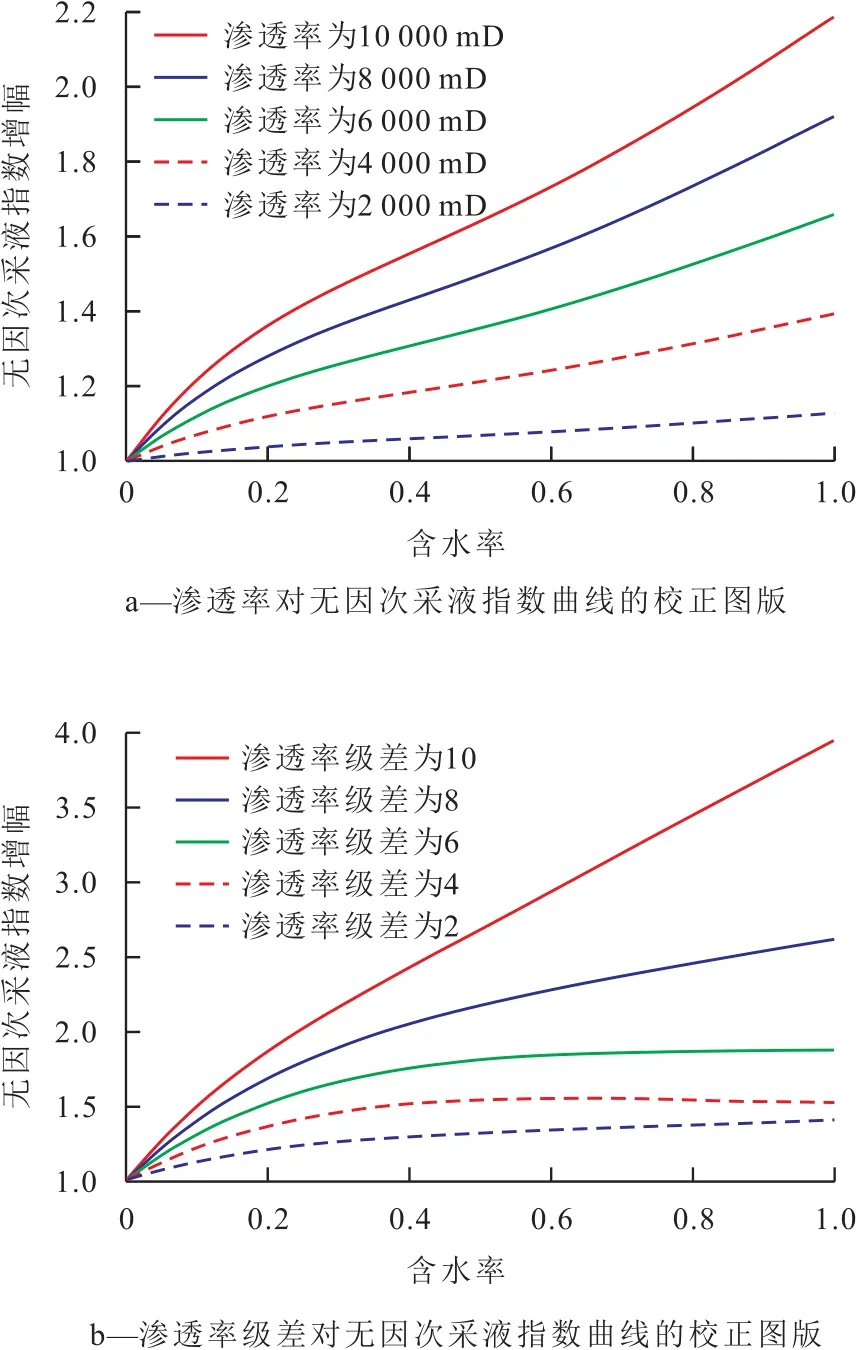
图1 考虑渗透率及渗透率级差的无因次采液指数曲线校正图版Fig.1 Correction of dimensionless liquid production index curves in consideration of permeability and permeability ratio

2 非均质油藏无因次采液指数变化规律的预测方法

基于岩心实验数据计算的无因次采液指数反映了水驱波及区的采液能力，在预测实际油藏采液能力变化规律和评价开采潜力时，还须考虑水驱未波及区的影响。

将油井水淹后的油藏划分为水驱波及区和未波及区2部分（图2）。其中，水驱波及区驱油过程包括初期压降漏斗形成阶段的弹性泄油和水驱阶段的水驱油，水驱油规律符合实验测试的油水相对渗透率曲线，但需要根据目标油藏的实际渗透率及渗透率级差，按照所建立的校正图版修正无因次采液指数曲线；对于水驱未波及区，仅存在弹性泄油，采液规律符合弹性驱动的物质平衡方程。

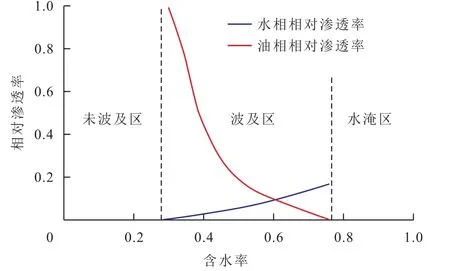
图2 非均质油藏水驱波及区与未波及区划分及流动特征Fig.2 Division of water flooding sweep region and flow characteristics of heterogeneous reservoirs

3 实例分析

中国东部某断块油藏中的Ⅰ，Ⅱ类储层平均地层渗透率为3 270 mD，渗透率级差为5.7，获取的典型岩样平均渗透率为793 mD，其油水相对渗透率曲线如图2。该油藏在综合含水率为98%时进行综合挖潜调整，此时矿场的油井无因次采液指数约为5，远低于根据岩心相对渗透率测试数据计算的理论值（约为18）。运用新建立的方法预测该油藏采液能力的变化规律，并测算该油藏水驱波及系数，为挖潜提供可行性依据。

将目标油藏划分为水驱波及区和未波及区，预测这2部分在并联的条件下油藏的整体采液能力随含水率的变化规律。计算步骤如下：①根据典型岩样的相对渗透率曲线（图2）绘制理论无因次采液指数曲线（图3）。②根据渗透率及级差，由新建立的图版法绘制无因次采液指数的校正曲线（图3）。③设定不同波及系数，按照并联模式计算油藏的整体无因次采液指数。④根据理论曲线与矿场监测数据的拟合程度，确定油藏水驱波及系数（图4）。对比分析结果表明，目标油藏在当前高含水阶段其水驱波及系数约为0.4，潜力较大。

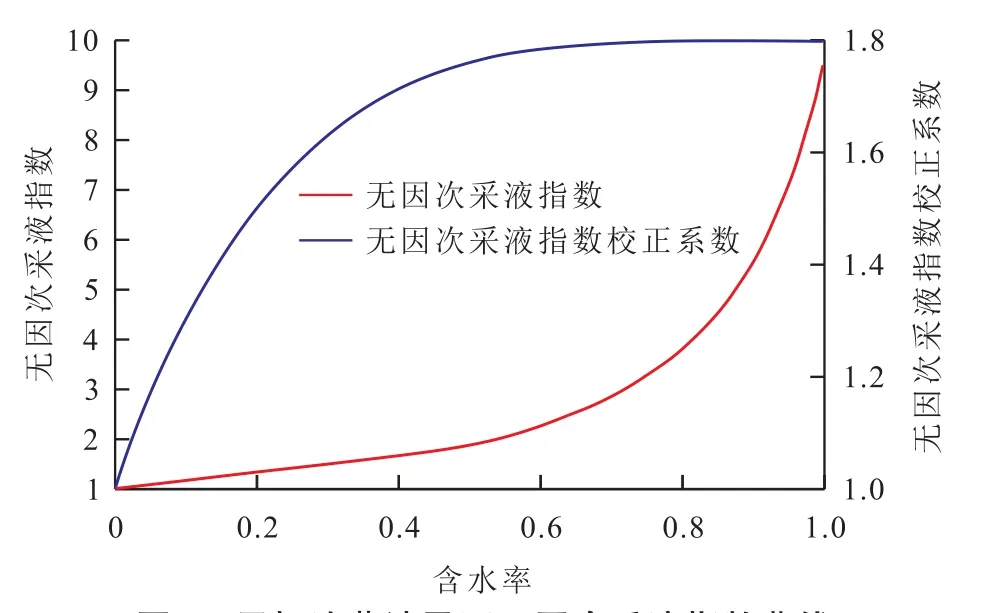
图3 目标油藏波及区无因次采液指数曲线Fig.3 Dimensionless fluid production index curve of target reservoir in water flooding sweep region

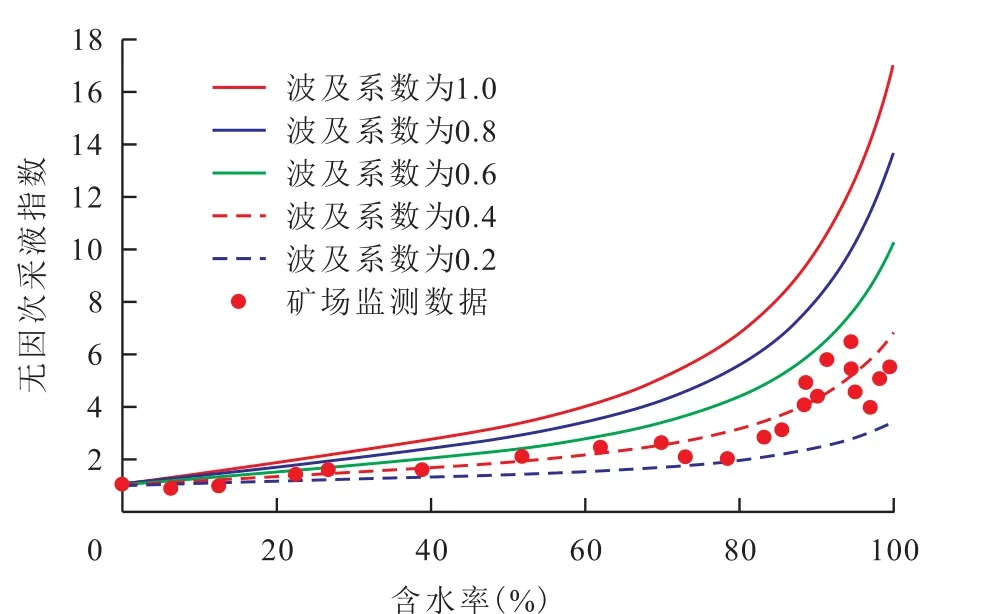
图4 图版法测算目标油藏水驱波及系数Fig.4 Sweep efficiency of water-flooding reservoir with crossplot method

4 结论

基于岩心并联水驱油实验数据，建立无因次采液指数曲线的经验公式及考虑物性及非均质程度对采液能力影响的图版，并将水驱油藏划分为水驱波及区和未波及区，建立非均质油藏采液能力的预测方法；研究结果表明：储层的非均质程度降低了水驱油的波及系数，进而导致油藏的整体采液能力随非均质程度的增加而降低；对比矿场监测的油井采液能力变化规律，利用所建图版可以测算水驱油藏的水驱波及系数，从而为挖潜调整提供理论依据。新建立的方法所需参数较少，充分利用了岩心驱替实验数据，能够考虑储层物性及非均质性对驱油过程的影响，并可根据矿场数据快速评价水驱效果和预测合理采液规模。

符号解释

JLD——无因次采液指数；a,b,c——无因次采液指数曲线方程系数；fw——含水率；A1,A2,B1,B2,C1,C2——无因次采液指数曲线方程关于渗透率的方程系数；K——渗透率，mD；KD——渗透率级差。