基于QR-GED-EGARCH模型的上证180指数风险度量分析

卞 蕾 王慧龙 胡梦婕

（安徽大学 ，安徽 合肥 230601）

一、引言

近年来，随着金融创新的深化和经济金融全球化趋势的加强，使金融市场更加动荡，金融机构面临的风险加大。“2017中国金融风险管理高峰论坛”提出要将金融风险管理从日常管理提升为战略管理，逐渐成为整个金融体系运行和管理的核心。VaR方法，作为一种金融风险管理工具，它利用统计思想对风险进行估值，该方法在风险测量、监督等领域被广泛应用，成为市场风险测量的主流方法。

VaR是金融头寸在给定一个时间段内一定置信水平下的最大损失。对VaR值的计算实质上就是研究序列的波动率，针对收益率序列呈现的尖峰厚尾、波动集聚性及不对称性特征，利用GARCH族模型来拟合。国内外许多学者做了很多关于金融时间序列风险度量的研究，ARCH模型最开始由Engle[1]提出，随后Bollerslev[2]在此基础上，将过去的条件方差引入条件方差模型得到了GARCH模型；由于杠杆效应的存在，Nelson[3]提出了EGARCH模型，该模型能准确地描述金融序列呈现的非对称性特征。GARCH模型族都是假定收益率序列服从某一分布下进行VaR度量，研究表明，基于正态分布下VaR参数法在一定置信水平下计量VaR时会严重低估风险，在对正态分布提出质疑后，研究人员进行了大量的探索，陆续提出偏 t分布[4]、广义误差分布[5]、Pareto 分布[6]、稳定分布[7]、g-h分布[8]等，并将其应用到风险度量中。以上研究在一定程度上解释了收益率序列存在的尖峰厚尾以及波性集聚特征，却不能全面度量收益率序列的风险。Engle和Manganelli[9]提出了基于分位数理论进行度量VaR的CAViaR模型,无须对尾部分布等进行假设，直接对VaR本身进行建模。Chen和Kang[10]将CAViaR模型用于对股市风险度量研究中，陈耀辉和朱盼盼[11]将其应用到汇率风险研究中,将GARCH模型与分位数回归模型相结合进行比较分析。刘亭和赵月旭[12]利用QR-t-GARCH模型对沪深指数收益率进行了风险度量研究，结果发现加入分位数回归的GARCH（1，1）模型较 GARCH（1，1）对收益率风险度量效果更好。简志宏等采用了CAViaR-EVT模型对极端隔夜风险进行预测，实证结果表明其预测效果比EVT和GARCH-EVT模型更合理[13]。曾裕峰和张涵[14]分别采用CAViaR模型和GARCH模型对VaR进行风险建模，结果发现CAViaR模型在股指期货风险预测方面具有明显优势。分位数回归理论应用于VaR计算可以比较全面地度量收益率序列的风险，也无需假定服从任何分布，是一种半参数估计方法。有关GARCH族模型和分位数回归模型相结合的研究较少，大量研究还是集中在两种方法的孤立应用上。

而针对存在杠杆效应所提出的EGARCH模型，它在与分位数回归结合后，其度量风险的精确度是否高于EGARCH模型？本文利用GARCH模型和EGARCH模型并将分位数回归结合构造的QRGARCH、QR-EGARCH模型，在考虑上证180指数收益率序列服从正态分布、t分布、偏t分布、GED分布、偏GED分布的情况下，选取1%和5%两个不同的置信水平，以求找到最优的拟合模型。

二、模型与VaR方法

（一）GED-EGARCH 模型

GARCH模型在处理金融时间序列时存在一些弱点，如要求无条件方差必须非负以及它对正负扰动的反应是对称的。为了克服这些弱点，Nelson提出了EGARCH模型，该模型既放松了对GARCH模型参数的非负性约束，又反映了杠杆效应，GED分布是一种更为灵活的分布形式，通过对其参数的调整，GED分布的尾部厚薄也会有所变化，能更好地处理收益率的厚尾现象。

（二）QR-GED-EGARCH（1,1）模型

分位数回归 （QR）描述的是当给定回归变量X时，响应变量Y在不同分位数下的变化趋势，该思想最早是由Koenker和Bassett[15]提出来的，它是将响应变量看作是其他变量的线性函数，从而推导出回归系数的渐近分布，Taylor[16]将分位数回归应用到VaR的计算上，其表达式为：

Chen[17]利用上述思想，对日经225股票指数进行具体分析，利用分位数回归方法，将收益率作为响应变量，K和作为回归变量对收益率序列进行相关风险度量。

借鉴上述研究，本文采用模型如下：

其中，σt的估计值的值由GED-EGARCH（1,1）模型得到，βτ的估计值由分位数回归法通过求解以下公式得到：

（三）VaR的计算原理

VaR又称风险价值，它可以定义为金融头寸在给定一个时间段内一定的置信水平下发生的最大损失。即，假设 F（x）为的积累分布函数，且该金融头寸的收益率分布下侧分位数为，那么VaR在置信水平1-下的计算公式为：

三、上证180指数收益率的实证分析

（一）数据选取与处理

本文选取上证180指数日收盘价作为研究对象，时间区间为2010年6月1日到2018年4月27日，本文把股票日收益率定义为

其中Pt表示股票指数日收盘价格，Rt表示日股票指数收益率序列，数据来源于同花顺软件，研究采用的软件有Eveiws9和R语言。

（二）上证180指数日对数收益率特征的检验

1.正态性检验

上证180指数日对数收益率的基本统计特征分析如表1所示：

表1 收益率的描述性统计量

由表1可知，上证180指数对数收益率序列偏度为-0.721,23，小于0，说明序列分布有长的左拖尾。峰度为8.813,84，远高于正态分布的峰度值3，说明收益率序列具有尖峰和厚尾的特征。Jarque－Bera统计量为2,872.005，值近似为零，拒绝该对数收益率序列服从正态分布的假设。为了更直观地看出序列的尖峰厚尾和不服从正态分布的特征。下面做出上证180指数日对数收益率的Q-Q图和分布拟合图。

图1显示，QQ图偏离直线的程度较高，可以认为样本数据不服从正态分布。且从图2可以看出，收益率分布对比正态分布具有很明显的尖峰厚尾特征，故不能用正态分布来拟合数据分布，而需要用其他的分布去估计GARCH模型的参数。

2.序列自相关性检验与平稳性检验

对收益率的自相关性进行分析，发现大部分样本自相关系数和偏自相关系数都在零值附近波动，且由Q统计量及其伴随概率可知，在5%的显著性水平下，接受原假设，即收益率序列不具有自相关性。接下来，对该序列进行ADF单位根检验，检验结果如表2所示：

图1 上证180指数正态Q-Q图

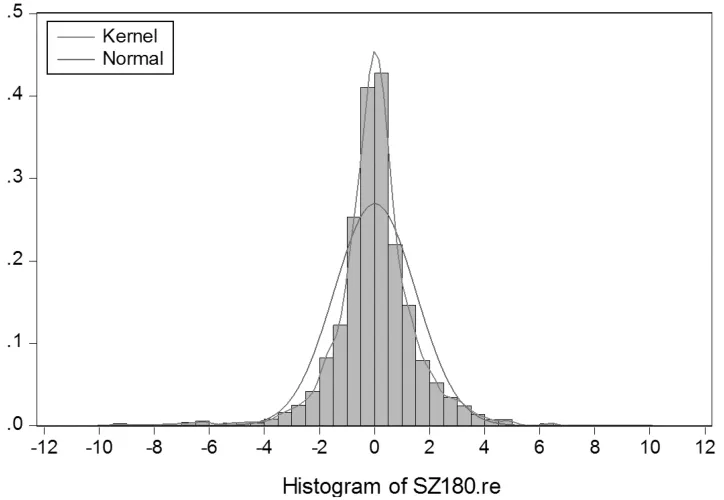
图2 上证180指数收益率分布拟合图

表2 数据的单位根检验结果

其中，t统计量的值为-42.315,80，对应P值接近0，表明序列平稳。在1%、5%、10%的显著性水平下，上证180收益率序列均拒绝随机游走的假设，说明该序列是平稳的。

3.ARCH效应检验

图3 上证180日对数收益率

由图3可以看出股指收益序列呈现出一种波动的聚集性，从直观上看序列可能存在异方差性以及杠杆效应。对序列进行LM检验异方差性，结果如下表3所示：

表3 LM异方差检验

（三）模型的建立与估计

1.GED-GARCH（1,1）模型估计及计算

由上述分析可知，收益率序列具有分布的尖峰厚尾性，波动的集聚性以及信息不对称性特征。因此建立GED-GARCH模型对收益率序列进行估计，滞后阶数（p,q）选择（1,1）。 将其与基于正态分布、t分布、偏t分布、GED分布和偏GED分布的GARCH、EGARCH模型相比较，通过比较 AIC、SC值，选出最优模型，其检验结果如下表所示：

由信息最小化准则可知，建立收益率序列服从GED分布的EGARCH模型效果最佳，估计参数的结果如表4所示：

由表5结果可知，除参数均值μ以及非对称系数γ不显著外，其余参数均显著，具体构建的 GEDGARCH（1,1）模型结构如下所示：

由此模型可以看出：α+β>1，说明收益率的波动具有持久性，当前信息对预测未来的条件方差有重要意义；γ<0，说明了相同单位的利坏信息冲击对波动的影响要比利好信息冲击来的大。接下来，对得到的模型进行检验，标准化后的残差过程的统计量为 Q（10）=17.670（0.061）和 Q（20）=24.348（0.228），而平方过程，其对应的统计量为Q（10）=14.199（0.164）和 Q（20）=21.083（0.392），括号中的参数是其对应的P值。因此，在拟合的标准残差序列中不存在相关性，说明所拟合的模型是合适的。

综合以上分析，基于GED分布的EGARCH模型对比其他分布下的模型能更好的拟合收益率的波动。

下面，利用VaR的计算公式，在给定分位点为0.05和0.95的情形下，计算出了GED-EGARCH（1,1）模型的值，并作出动态走势图（如图4）。

2.QR-GED-GARCH（1,1）模型的建立

在上文所得到的GED-GARCH （1,1）模型基础上，现将分位数回归方法应用到该模型中，由2.2节方法可知，模型的结构为：

表4 AIC、SC值比较

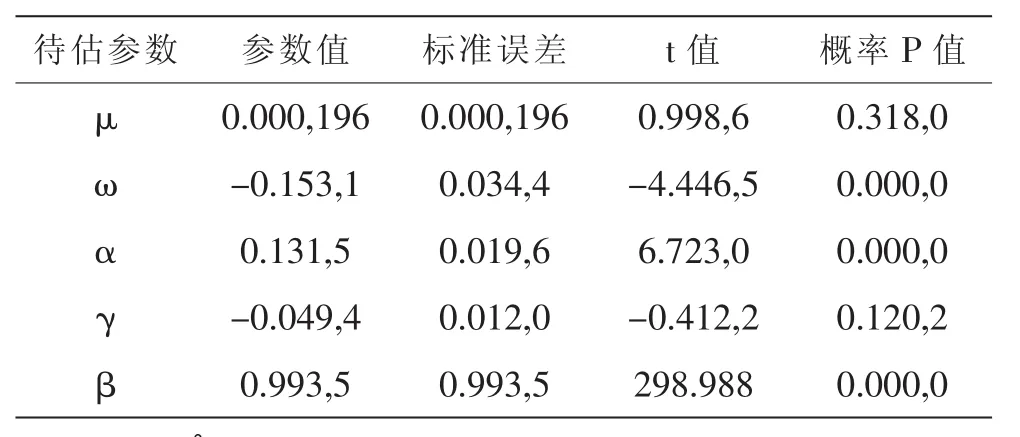
表5 基于GED分布的EGARCH模型估计参数表

图4 GED-GARCH（1,1）模型动态走势

图5 两类模型动态走势比较图

由图5可以很明显看出，分位数取0.5时，VaR值的波动变化很不明显，其趋势图趋近于一条直线，在分位点为0.05，0.95时，其波动效果明显，且与实际收益率的波动值趋势一致，这也说明了分位数回归模型不仅能对股票收益率序列进行全面描述，而且对其尾部特征能进行更好的描述，也适应了金融时间序列高峰厚尾的特点。比较两类模型的走势可以发现，在分位点0.95时，两类模型变化趋势趋于一致，而在给定分位点为0.05，其对应95%置信水平下时，两类模型的值波动的程度大小有较大差别，这说明对于极端情况下，对损失的敏感程度要高于收益，特别是在股票价格剧烈波动的时间区间里，加入分位数回归后的模型避免了过于低估风险值，对风险有一个更为精确的刻画。

（四）VaR的检验—Kupiec检验

通过模型进行预测后，需要对其预测值进行检验，来检验所构建模型的有效性。下面利用Kupiec[18]提出的似然比率检验法比较不同模型预测能力的可行性水平。假定考察天数为N，失败天数为n，那么失败频率则为α*=N/n，我们所期望得到的预测结果为失败频率等于所给定VaR的置信水平α。模型估计太过保守，高估了风险。为此，Kupiec检验原理所建立假设如下，原假设和备择假设分别是：

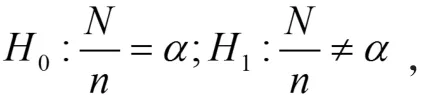
似然统计量为：

在原假设H0成立的条件下，似然统计量服从自由度为1的卡方分布。若出现失败次数过多或者过少这样的极端情况，则会拒绝原假设，模型失效。

由表6和表7失败率检验结果，可以得出如下结论：

第一，针对GARCH族模型中同一模型的不同分布。在5%的显著性水平下，基于t分布下模型的失败天数少于基于GED分布下的模型，但其拟合成功率低于基于GED分布下的模型，说明在t分布下模型低估了风险。而在1%的显著性水平下，基于t分布下模型的失败天数要高于基于GED分布下的模型，其似然比率检验中P值均小于显著性水平0.01，拒绝原假设，此时的t分布高估了风险，t分布无法在上证180指数风险度量中提供有价值的信息。且不管是在1%还是在5%情况下，GED分布均通过了检验，可见GED分布相比于t分布更能刻画上证180指数收益序列的分布特征。

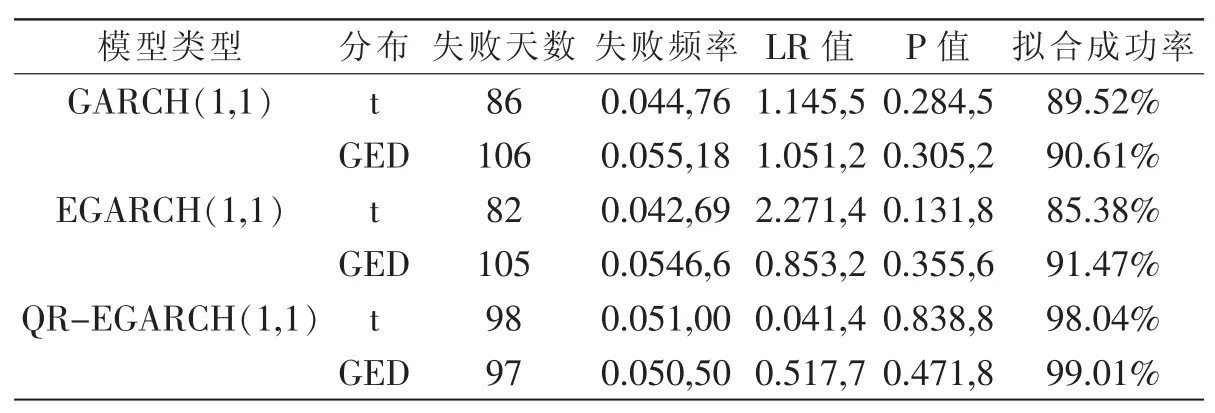
表6 5%显著性水平下三种模型VaR失败率检验

表7 1%显著性水平下三种模型VaR失败率检验

第二，对于GARCH族模型同一分布下不同模型，从似然比率LR统计量结果分析，基于t分布下的EGARCH模型并未表现出比传统GARCH模型更优越的风险测度能力。而在基于GED分布下EGARCH模型的拟合成功率高于传统GARCH模型，这说明了t分布与传统GARCH模型结合，GED分布与EGARCH模型结合应用于风险度量中更合适。在5%的显著性水平下，GED-EGARCH（1,1）模型的预测精度要优于其他三类模型，其拟合成功率达到了91.47%，说明了GED分布和EGARCH模型的结合能很好地描述上证180指数所存在的尖峰厚尾、波动集聚性以及杠杆效应。

第三，在上述基础上，将分位数回归引入到EGARCH模型中，其预测精度有了显著地提高，且明显高于前两类模型。可以很明显看出QR-GED-EGARCH（1,1）模型对上证180指数风险的预测效果较其他模型表现更为优异。

综上所述，由于分位数回归模型无须事先设定误差分布函数的特定形式，并能全面地度量风险，其与GED-GARCH （1,1）模型结合后所构造的QRGED-EGARCH（1,1）模型，对上证180指数收益序列的风险有更为精确地测度。

四、结论与思考

本文在运用分位数回归方法以及考虑收益率序列具有杠杆效应的的情况下构建了QR-GED-EGARCH模型，对上证180指数收益率序列风险值进行了动态建模分析，并与基于t分布和GED分布下的GARCH和EGARCH、以及QR-t-EGARCH进行比较，利用Kupiec检验来比较各个模型拟合收益率序列的准确程度。研究结果表明，从序列波动性特征来考虑，应用EGARCH模型对风险值进行测算，较好的反映了上证180指数收益率序列所具有的“杠杆效应”，且收益率序列拒绝服从正态分布的假设，故利用了能描述序列尖峰厚尾特征的t分布和GED分布，Kupiec检验结果表明基于GED分布下的模型其预测精度普遍高于t分布下的模型，在此基础上，引入分位数回归后所构建的QR-GED-EGARCH模型拟合成功率为99.01%，优于其他模型，说明其QR-GED-EGARCH全面地描述收益率序列特征，并且对风险值有一个精确的刻画。