复杂形状焊缝疲劳裂纹演变过程仿真
2019-09-28魏国前李山山
叶 凡 ,魏国前 ,2,余 茜 ,李山山
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北武汉430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北武汉430081)
0 前言
疲劳断裂失效涉及裂纹萌生、裂纹扩展和疲劳断裂三个阶段。对焊接结构而言,产品初期往往包含若干类裂纹缺陷[1],其裂纹萌生阶段一般较短并可被忽略。因此焊接结构的疲劳寿命常常被定义为裂纹的扩展寿命,深受裂纹扩展行为的影响。
国内外很多学者都对疲劳裂纹的扩展行为展开过研究。刘荣伟等[2]采用相互作用积分法模拟了高强度钢疲劳裂纹扩展,拟合得到裂纹的扩展速率曲线。Nasri等[3]利用扩展有限元法研究了三种双材料合金裂纹扩展速率的差异性,并对疲劳寿命进行比较。周素霞等[4]使用ANSYS软件建立了动车组铸钢制动盘三维瞬态计算模型,对已产生裂纹制动盘的疲劳寿命进行了预测。范磊等[5]将裂纹扩展过程离散化处理,得到了直升飞机行星架剩余寿命与裂纹长度的变化关系,利用有限元软件疲劳模块验证了计算结果。上述有关裂纹的仿真研究主要偏重扩展寿命与尺寸的关系,未考虑裂纹真实的形状演化过程,无法准确预测焊接结构的疲劳性能。余茜等[6]针对十字焊接接头开展了疲劳裂纹的扩展仿真研究,分析不同初始裂纹下疲劳裂纹的扩展行为,揭示了初始裂纹位置对疲劳裂纹扩展的影响规律。Tanaka等[7]采用两种数值计算方法模拟T型焊接接头表面裂纹扩展,并将模拟结果与试验进行对比。这些研究主要针对平直焊缝,研究方法和成果无法直接用于工程中的复杂形状焊缝。
为此,本文针对具有复杂形状焊缝的焊接结构,基于线弹性断裂力学方法,采用半圆形初始表面裂纹,提出了一种焊趾裂纹演变过程的仿真方法。以某波纹腹板梁为例,模拟曲线焊缝上焊趾裂纹的完整演变过程,分析了裂纹前沿形状、应力强度因子和疲劳寿命等疲劳行为。
1 裂纹扩展仿真原理
1.1 裂纹扩展模型
常用的裂纹扩展模型有Paris模型、Walker模型和Nasgro模型等。其中,Walker模型和Nasgro模型是在Paris模型的基础上,分别考虑应力比和裂纹张开效应的影响修正得到。对于焊接结构,应力比的影响较小,可忽略不计。在一定的裂纹尺度下,裂纹的张开效应也可忽略不计。Paris模型考虑了应力强度因子范围对裂纹扩展速率的影响,本文认为是疲劳裂纹扩展的主要控制参量,因而采用Paris[8]模型对疲劳裂纹扩展进行预测仿真,其表达式为
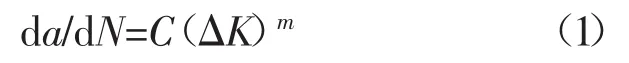
式中 da/dN为裂纹扩展速率;C和m为描述材料疲劳裂纹扩展性能的基本参数,由实验得到;ΔK是应力强度因子范围。
1.2 应力强度因子的计算
断裂力学理论中,应力强度因子K是反映裂纹尖端应力场强弱的重要参量,一般可采用解析法、数值法和有限元法进行求解。由于工程结构形状和载荷条件复杂,有限元法应用较为广泛。同时,为了避免裂纹尖端的应力奇异性,常常采用J积分理论间接求解应力强度因子K。
对于焊接结构,焊缝局部细节的应力状态往往呈现混合模式,需要同时考虑KⅠ、KⅡ、KⅢ的混合作用。本文采用Knowles[9]提出的M积分法,与J积分理论相似,K积分也与求解路径无关,表达式为

相较于J积分,M积分可同时计算出三种断裂模式下的应力强度因子,M积分与应力强度因子之间的关系为
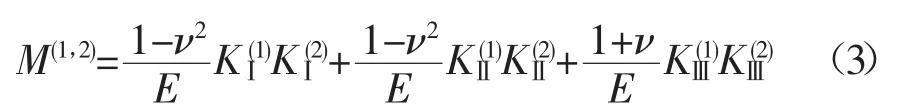
式中 E为材料的弹性模量;ν为泊松比;KⅠ、KⅡ、KⅢ为三种载荷形式下对应的裂纹尖端应力强度因子。
1.3 裂纹扩展原理及其方向准则
裂纹扩展原理如图1所示。首先,将当前裂纹前沿离散成若干个点,指定中间点的扩展步长,根据裂纹前沿各点应力强度因子增长量与中间点应力强度因子增长量之间的比例关系,推算其他各点的扩展长度,从而预测下一个裂纹前沿的几何信息。其表达式为

式中 Δa为裂纹前沿的扩展步长;ΔK为裂纹前沿的应力强度因子幅值;R为应力比;下标median和i表示裂纹前沿中间点和裂纹前沿第i点。
在扩展过程中,裂纹扩展方向对计算下一步的应力强度因子具有很大的影响。在“张开型”模式下,裂纹将沿原始裂纹平面上扩展。在复杂情况下,裂纹的扩展方向将发生偏转且不易预测。为了模拟真实裂纹扩展行为,采用三种常见裂纹扩展方向准则。
(1)MTS(Max Tensile stress)准则:该准则认为裂纹主要沿周向应力最大的方向延伸。
(2)GEN(Generalized Stress)准则:该准则同时考虑了裂纹所受到的最大周向应力和最大剪应力的影响。
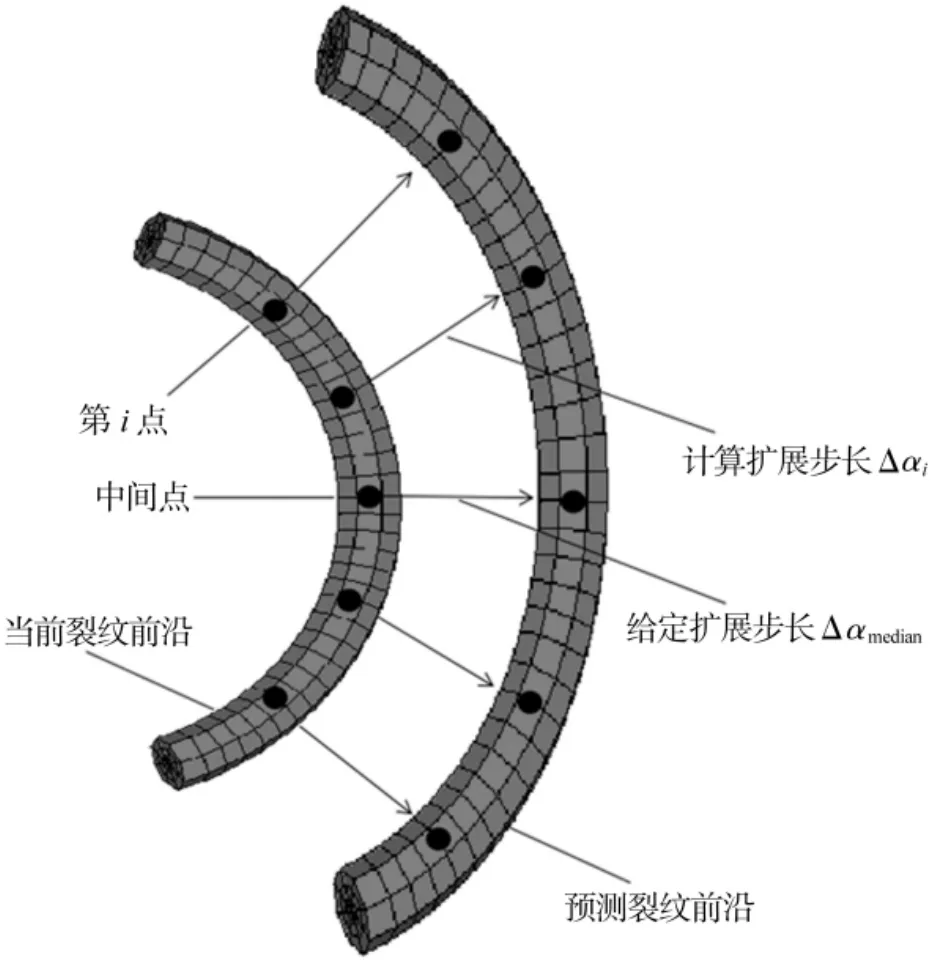
图1 裂纹扩展原理示意
(3)SERR(Strain Energy Release Rate)准则:该准则认为裂纹将在应变能释放率最大的方向上扩展。
2 仿真实例
2.1 对象描述
以参考文献[10]中波纹腹板梁疲劳试验为例,采用上述方法开展仿真研究。该试验对象的几何参数如图2a所示,其中:上下翼缘厚度为20 mm,中间腹板厚度为6 mm,通过4道焊缝相连接,焊缝尺寸为6 mm。图2b为截取的一段焊缝,它由平行段、倾斜段以及两者之间的过渡圆弧段组成,曲线形状比较复杂。此种曲线焊缝不仅会导致焊趾局部应力状态复杂,还会带来加工上的不便,导致焊接质量低劣。文献[10]提供的波纹腹板梁试件的实际焊缝外观如图2c所示,可明显看到焊趾曲线的不连续性,这些几何上的缺陷将极大影响焊接结构的疲劳性能。
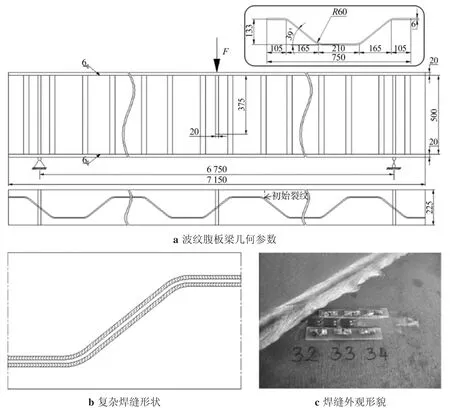
图2 仿真对象[10]
根据文献,波纹腹板梁试件在三点弯条件下开展疲劳试验,Fmin=10 kN,Fmax=240 kN。材料为S355,重要力学参数为[11]:C=5.21×10-13MPa·mm1/2,m=3,ΔKth=63 MPa·mm1/2,KIC=1 581 MPa·mm1/2。
2.2 含裂纹体子模型的建立
考虑到焊缝形状对焊趾裂纹演变行为有直接影响,全部采用C3D20R单元建立波纹腹板梁有限元模型。根据Radaj[12]的研究,初始裂纹形状比不影响其后的形状演变。此处采用半圆形模拟初始裂纹的形状,如图3a所示,定义半圆形初始裂纹深度a=0.5 mm,则裂纹表面长度2c=1。根据文献[12],疲劳裂纹萌生于下翼缘与腹板的连接焊趾上,具体位置为跨中偏右第二个波纹段中焊趾圆弧段与倾斜段的交点附近,如图2a中标注所示。考虑到波纹腹板梁整体单元尺寸与裂纹区域单元尺寸差异较大,直接建模将会导致巨大的计算量,因此采取子模型技术。将涉及裂纹扩展的部分区域切分出来,如图3b所示,在裂纹萌生位置插入初始裂纹,初始裂纹面平行于焊趾线且垂直于下翼缘上表面。在裂纹扩展的不同步长内,仅需在该区域内重新添加新裂纹并为其划分细密网格,如图3c所示。裂纹前沿网格模型如图3d所示,采用3层单元模拟该区域。其中:第1层模拟裂纹前沿的最内圈,采用15节点奇异楔形五面体单元;第2层和第3层为20节点六面体单元环。这些楔形单元和六面体单元组合起来共同模拟整个裂纹前沿区域的力学行为。其余区域采用10节点四面体单元,四面体单元和六面体单元之间使用13节点的金字塔过渡单元。
2.3 裂纹扩展仿真过程

图3 模型网络图
完整的裂纹扩展仿真过程如图4所示。首先建立波纹腹板梁实体模型,切分出裂纹扩展区域的子模型。然后在子模型中插入初始表面裂纹,建立含裂纹体仿真模型。接着根据裂纹扩展原理在不同时间步长内计算相应的裂纹前沿点的扩展步长和裂纹前沿的形状,依次循环下去,直至撕开下翼缘时停止仿真。
裂纹扩展过程中,控制扩展步长Δamedian非常重要。扩展初期,裂纹增长较为缓慢,故将此时的裂纹扩展步长定为0.1 mm。在之后的扩展过程中,根据裂纹尺度的变化逐步增加扩展步长,依次设为0.2 mm、0.4 mm、0.8 mm、1 mm。当裂纹扩展至几何边界例如进入焊缝区域、穿透板厚时,需要根据实际情况实时调整扩展步长。

图4 裂纹扩展流程
3 结果与分析
3.1 裂纹演变路径
采用三种裂纹扩展方向准则,获得了三种裂纹扩展的仿真结果。其中MTS准则的仿真结果与试验结果最为一致,裂纹形貌如图5所示,三点弯曲循环加载条件下波纹腹板梁的疲劳裂纹扩展行为主要由最大拉应力控制。

图5 裂纹形貌
根据仿真结果,波纹腹板梁的焊趾疲劳裂纹扩展可以分为以下三个阶段(见图6)。
第一阶段,裂纹在靠近焊趾处沿焊缝方向和裂纹深度方向同时扩展,裂纹前沿形状由半圆形逐渐演变为半椭圆形,直至偏离焊趾方向,这一阶段扩展长度很小,寿命却较长。
第二阶段,裂纹一端离开焊趾,沿与梁纵向成3°~5°夹角方向扩展至翼缘侧边,另一端则向焊缝内插入,并扩展至翼缘另一侧以及腹板上,这一阶段由于焊缝材料和腹板材料的增加,裂纹面超出半椭圆面积。
第三阶段,当裂纹深度贯穿下翼缘板厚时,以贯穿裂纹的形式在翼缘和腹板上扩展,扩展速率非常快,裂纹很快撕裂一侧翼缘板。
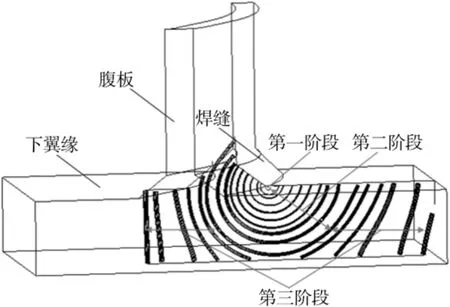
图6 裂纹扩展动态示意
3.2 应力强度因子
在裂纹扩展过程中,裂纹前沿形状不断在发生变化。为了描述裂纹前沿应力强度因子的变化趋势,将所有扩展过程中的裂纹前沿进行归一化处理,即:将裂纹前沿两个端点的曲线坐标分别定义为“0”和“1”,其余各点的曲线坐标则根据该点所在位置占整个裂纹前沿曲线长度的比值,在“0”到“1”之间线性变化。各阶段裂纹前沿示意如图7所示。

图7 各阶段裂纹前沿示意
3.2.1 KⅠ
第一、二阶段裂纹扩展过程中,裂纹前沿呈现半椭圆形状,因此将这两个扩展阶段统一进行分析。提取第一、二阶段不同扩展时期整个裂纹前沿应力强度因子KⅠ,如图8所示。其中:在第一阶段,裂纹前沿两端点(“0”和“1”)分别对应裂纹在焊趾曲线上的扩展;在第二阶段,两端点分别对应裂纹在焊缝纵向(或腹板纵向)和翼缘外侧方向的扩展;中值点(“0.5”)均对应裂纹在翼缘深度方向的扩展。
由图8可知,在裂纹扩展前期,整个裂纹前沿的扩展速率基本恒定,并处于较小水平。进入第二阶段后,裂纹前沿右端的应力强度因子明显高于左端,并且这种变化随着裂纹的不断扩展更加明显,表明裂纹沿翼缘外侧的扩展速率逐渐超过裂纹沿纵向方向的扩展速率,这主要是由于裂纹左端遇到焊缝材料和腹板材料的阻碍所致。

图8 第一、二阶段不同时期变化趋势
提取第一、二阶段裂纹前沿两端点和中间点在整个扩展过程中的应力强度因子KⅠ,绘制应力强度因子KⅠ随裂纹扩展深度尺寸的拟合曲线,如图9所示。可以看出,第一阶段裂纹在各个方向的扩展速率都趋于增加,在第二阶段则出现偏离,裂纹前沿右端点和中间点的扩展速率保持增加且趋势不变,左端点的扩展速率则在穿透焊缝到达腹板之后逐渐减小。

图9 第一、二阶段不同扩展路径下的变化趋势
在第三阶段,半椭圆的裂纹前沿在翼缘下表面被切断,进而在两端各自形成一个新的裂纹前沿,将其分别定义为Crack front 1和Crack front 2(见图7)。分别提取Crack front 1和Crack front 2在位置“0”、“1”处的应力强度因子 KⅠ。由于裂纹已经贯穿下翼缘,不再具有深度方向的扩展尺寸,因此绘制应力强度因子KⅠ随扩展步数的曲线,如图10所示。这4条曲线近似反应了裂纹在下翼缘左右两端的上、下表面扩展的变化规律。可以看出,在第三阶段前期,裂纹在下表面的扩展速率高于上表面,裂纹前沿形状也逐渐由弧线演变为直线。后期,Crack front 2的应力强度因子KⅠ明显出现陡增,并很快导致该侧翼缘的撕裂。

图10 第三阶段不同扩展路径下KⅠ的变化趋势
3.2.2 KⅡ、KⅢ
分别提取裂纹在第一、二阶段各个扩展步长的应力强度因子KⅡ、KⅢ,如图11所示。从整体上看,KⅡ、KⅢ的数值远小于 KⅠ,KⅡ基本趋近于 0,KⅢ在第二阶段后期在裂纹前沿左端出现较小波动,表明在第一、二阶段扩展过程中,模式Ⅰ占主导地位,采用MTS扩展准则是合理的。
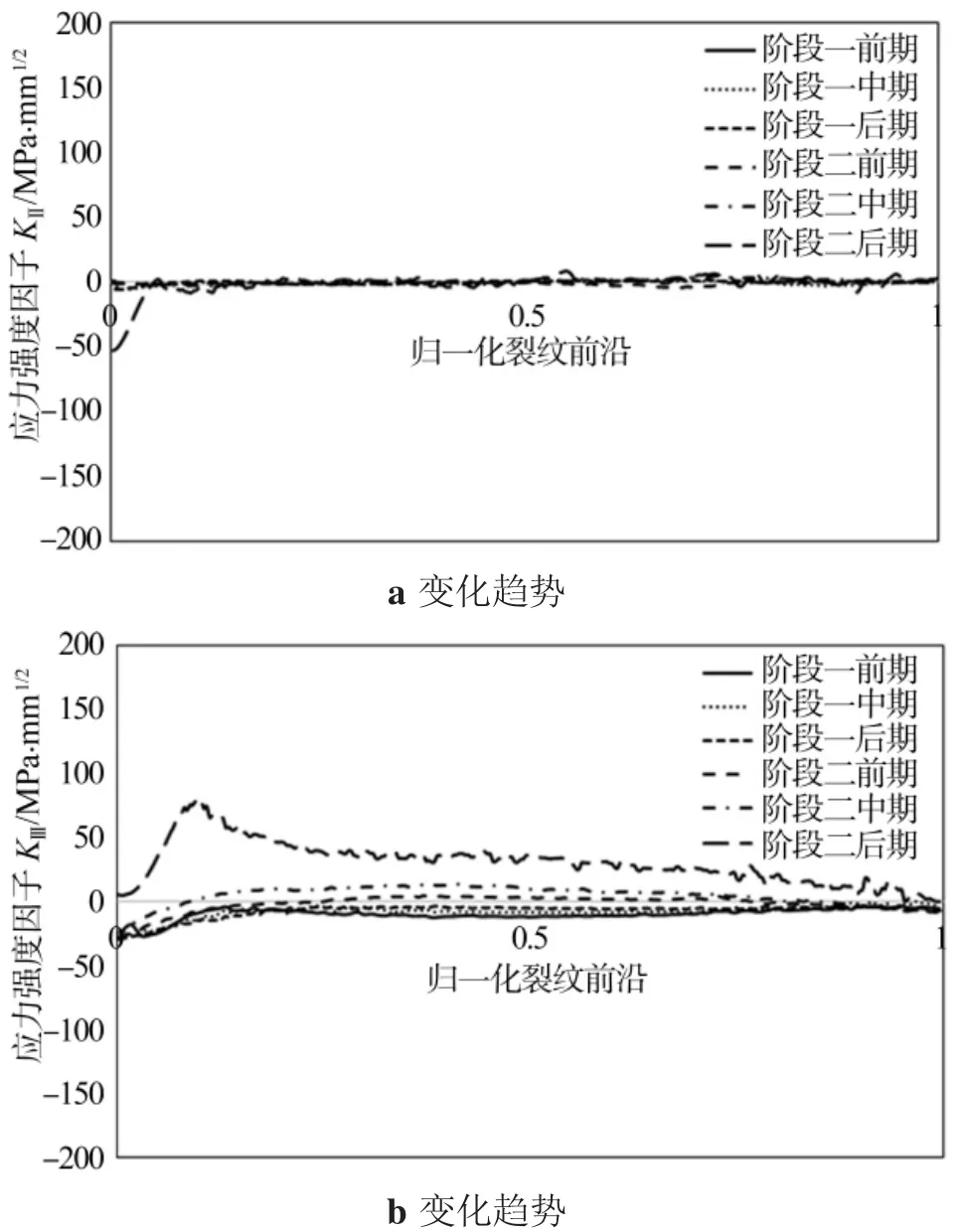
图11 第一、二阶段不同时期KⅡ、KⅢ变化趋势
第三阶段Crack front 1和Crack front 2应力强度因子KⅡ、KⅢ的变化趋势曲线与第一、二阶段类似,KⅡ的数值变化非常小,对裂纹扩展造成的影响几乎可以忽略不计。KⅢ有缓慢增加,但仍处于较低水平。
上述有关KⅡ、KⅢ的分析表明,波纹腹板梁疲劳裂纹在整个扩展过程中,模式Ⅰ占主导地位,因此采用MTS扩展准则是合理的。
3.3 扩展寿命
基于Paris速率扩展模型,采用Runge-Kutta[15]算法,得到了裂纹在三个阶段的扩展寿命,如表1所示。仿真得到三个阶段总寿命为112.21万次,文献中给出的试验寿命为130.95万次,寿命误差为16.7%。通过对比发现,第一、二阶段的扩展寿命占整个疲劳寿命的比重很大,第一阶段扩展深度虽然较小,但扩展寿命相对较大。
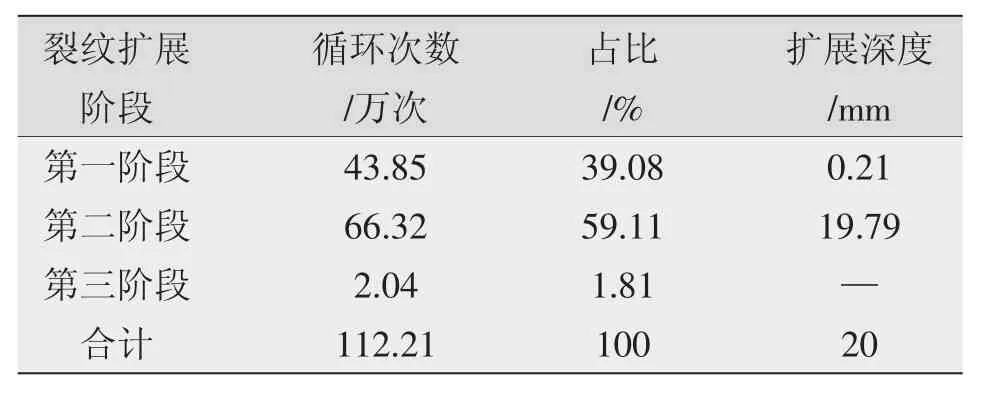
表1 不同阶段循环次数、扩展深度
4 结论
(1)提出了一种面向复杂形状焊缝结构的疲劳裂纹仿真方法,可以获得焊趾裂纹的完整演变过程,对裂纹扩展行为研究和寿命预测有重要意义。
(2)针对波纹腹板梁结构开展了疲劳裂纹的仿真研究,获得了裂纹形状的演变过程,揭示了裂纹扩展的典型阶段。
(3)分析了波纹腹板梁结构焊趾裂纹前沿应力强度因子的演变规律,讨论了裂纹扩展速率的变化特点,揭示了焊趾裂纹在不同阶段的扩展模式。
