水下湿法焊接直流电弧放电的仿真研究

李志刚 ，黄 卫 ，李 洋 ，徐 翔 ，叶建雄

（1.华东交通大学载运工具与装备教育部重点实验室，江西南昌330013；2.南昌工程学院机械与电气工程学院，江西南昌330099）

0 前言

目前对于陆地环境下的焊接电弧模拟研究基本采用磁流体动力学（Magnetothy drodynamics，MHD）方法和PIC（Particle-in-cell）方法。磁流体动力学方法是一种模拟等离子体电弧流动与传热的有效方法[1]。然而采用磁流体动力学方法解决水下焊接电弧的仿真存在很大困难，因为在液体电介质中（如水、油等），与在干燥气体环境中的击穿机理存在很大差异，导致无法获得相应的输运系数。PIC方法则是在基本方程为麦克斯韦方程组、洛伦兹力方程和牛顿运动定律下，模拟大量的微观粒子在外加电磁场及自生电磁场中的运动轨迹，再对物理量进行平均计算，得到等离子体的宏观性质及其运动规律的一种方法[2-3]，该方法十分耗费计算资源。

现今除了国外一些关于水下铜电极之间放电的研究[4]，电弧仿真研究多在干燥环境中进行。水下湿法焊接电弧的机理和模拟仿真尚在探索阶段。水下湿法焊接电弧发生在水中，等离子体通道通常被蒸汽气泡包围，该蒸汽气泡由于等离子体在放电阶段的压力增加而产生径向向外的膨胀[5]，因此需要探讨新的方法。本文在粒子物理学和静电学的新角度上建立了一种适用于液体介质中的直流电弧放电模型，从而对水下湿法焊接电弧进行仿真研究，并通过该电弧模型分析了在水下湿法焊接中的电弧形状。

1 水下湿法焊接电弧模型

水下湿法焊接区别于陆地和干法水下焊接的重要现象之一是电弧气泡。水下湿法焊接电弧气泡图像如图1所示，引弧产生的电阻热使电极与焊件间的水瞬间汽化，产生一个直径约为6～9 mm的核心阴极加热空化气泡[6]。因此将水中电弧导电通道由中心到外层划分为电离气泡、过渡层和液体层，其模型如图2所示。水溶液中，电离气泡为由阴极的电子、液体蒸发和电离的粒子和熔丝成分电离粒子等组成的等离子通道。在电离气泡周围，是蒸发和非蒸发水分子到未受影响的液体的过渡层，它由一些带电粒子和水蒸汽等组成。其周围是对气泡施以物理压力并且呈现电气绝缘性的液体（电介质）[7]。

图1 水下湿法焊接气泡图像[6]Fig.1 Underwater wet welding bubble image[6]

2 阴极电子发射和电弧静电场理论

水下电弧的产生依赖于阴极发射的电子，为了使电子获得足够的能量以破坏来自阴极表面的束缚力，阴极发射点必须达到足够的热发射温度。金属中的电子分布服从量子力学的费米能级函数，如（1）式所示：

图2 水下湿法焊接模型Fig.2 Underwater wet welding model

式中 m为电子质量；h为电子到发射面的距离；ε为一个电子总的能量；μ（T，n）e为化学势能；费米函数描述了电子在金属中的能级。积分式（1）可得到式（2）Sommerfeld的公式，它描述了饱和电流密度下的阴极电子热发射规律[6]。

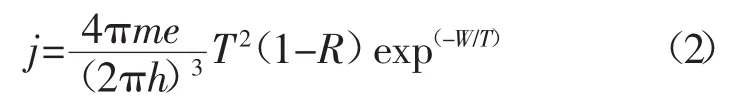
式中 j为饱和电流密度；e为一个电子电荷；T为阴极表面温度；R为电子反射系数；W为功函数。式（2）第一项被称作Sommerfeld或者是发射常数，如式（3）所示。

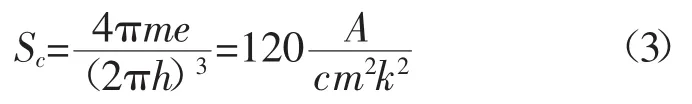
随着材料或特定条件的变化，发射常数将发生变化。在模拟仿真中，常常通过调整发射常数来匹配实验值。

电子由阴极发射后，进入三维静态电场，三维静态电场是螺旋场和旋转场的组合。静电电势用于估计电弧区域的静电场（不包括旋转部分），由泊松方程表示：

式中 V为电场电势；ε为介电常数；ρ为电荷密度（单位：C/m2）。

对于电流的分析采用如下相似的方程

式中 σ为电导（单位：S/mm）。

式中 J为电流密度；E为电场强度（单位：V/m）。

以上泊松方程方程可以在电磁分析软件Vector Fields采用有限元方法进行求解。

电磁分析软件Vector Fields中的Scala模块集合了用于计算电磁场和非线性方程的数值分析程序，可以计算三维空间中的静电场和空间电荷对带电粒子束的影响。

3 电弧有限元模型的建立及求解

电弧有限元模型运用电磁分析软件Vector Fields的Scala模块进行求解。该模块主要用于模拟电子束、粒子加速器、X射线的产生、辉光放电、带点粒子在各种媒介中的传递等。仿真步骤如下：

（1）定义仿真几何模型，包含电极形状、焊件位置等。

（2）确定和定义材料属性，如相对介电常数、电导率等。

（3）定义电场的边界条件，这里主要定义阴阳极电压。

（4）定义发射体以及发射机理，根据具体情况采用热电子发射或者场发射等。

（5）采用泊松方程等进行有限元计算。

首先，建立仿真几何模型，对应图2所示的水下湿法焊接模型，将水下介质分为电离气泡、过渡层和液体层，分别设置相应层的相对介质常数和电导率。采用的焊极是钨极，其形状尺寸为：阴极直径1.6 mm、尖角角度30°、尖角直径0.8 mm；电弧长度3 mm；阳极板厚度1.5 mm、直径15 mm。建立的仿真模型如图3所示。

图3 水下湿法TIG焊模型Fig.3 Model of underwater wet TIG welding

在建立模型网格时，因为阴极尖角的端部尺寸相对其他部位非常小，而模拟出的电子束的数量与阴极尖角端部网格的疏密度直接相关。所以需要在该部分单独细分网格，以保证模拟出的电子束数目满足仿真要求。发射极参数设置如图4所示，阴极尖角端部的网格划分更加密集，其余部分与发射出的电子束数量没有密切关系，可根据计算机的运算能力及计算时间进行合理选择。

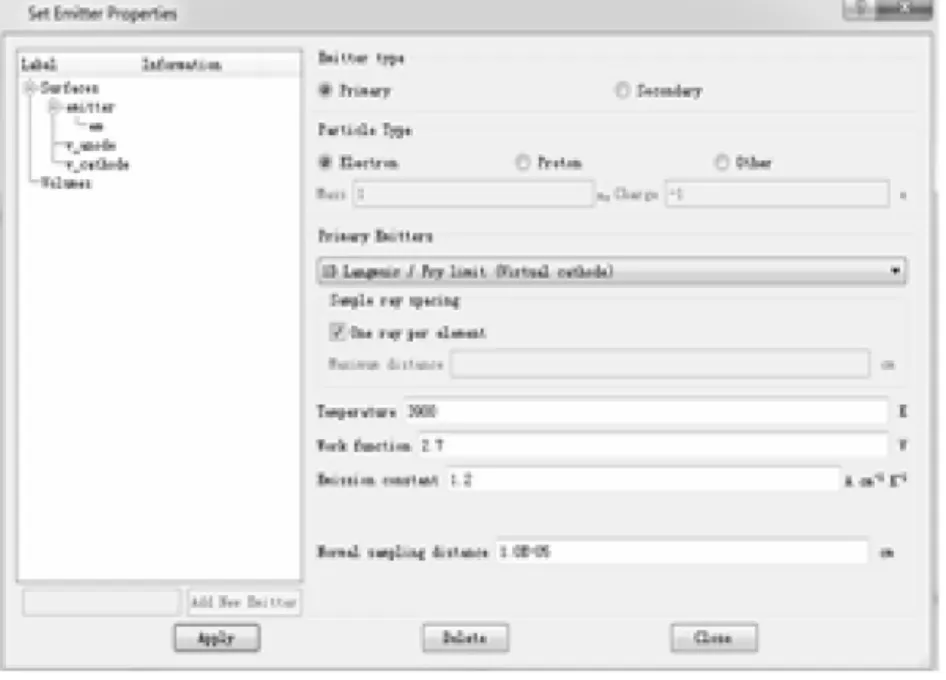
图4 发射极参数设置Fig.4 Setting parameter of emitting electrode

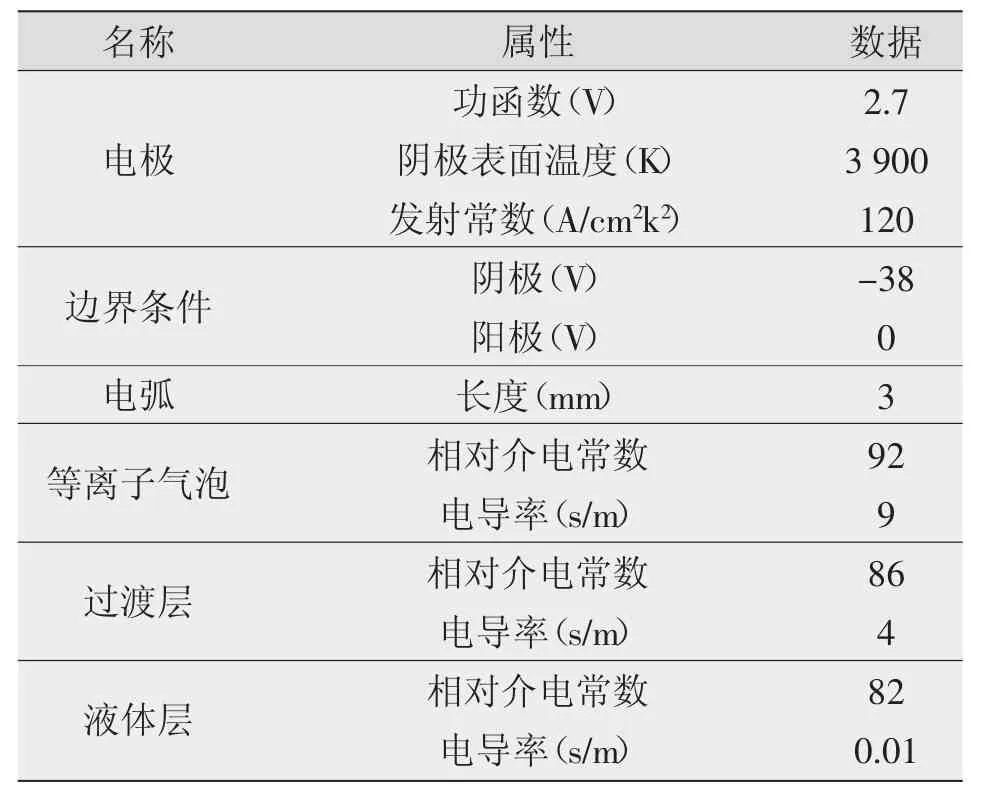
表1 水下介质中的模拟输入Table 1 Simulation inputs of underwater medium

关于电离气泡、过渡层和液体层电介质的参数，其相关研究很少，因此主要是从美国材料试验学会的分析及相关文献中[8]推断出来的。仿真时需要输入的数据参数如表1所示。

其次，电场的边界条件主要是电极表面的电压，借鉴相关文献所做的实验，空气中的TIG焊电极表面的电压取20 V，受水下高压条件的影响，为保证电弧的稳定燃烧，水下湿法焊接电极表面的电压取38V[9]。

再次，采用热电子发射机理，对应式（2），在电磁分析软件Vector Fields中设置电极为铈钨的功函数W=2.7 V、阴极表面温度3 900 K、发射常数A=120 A/cm-2K-2，如图4所示。最后采用有限元分析方法进行模型静态计算求解。

4 电弧轨迹形状的仿真结果

按以上模型及方法求得的水下TIG焊的电子轨迹如图5所示，考虑到水下电弧等离子体中电子速度为其他粒子的10倍数量级，数密度为其他粒子的107～108倍数量级，电子是水下焊接电弧中的主要产生效应的粒子，此处的仿真粒子主要针对电子粒子。所以此处仅考虑由电子束形成的电弧形状及电弧速度。由图5可知，其电弧呈“钟罩形”。水下TIG焊电子束的速度如图6所示。

图5 水下湿法TIG焊电子运动轨迹Fig.5 Beam trajectory of underwater wet TIG arc

图6 水下湿法TIG焊主电子束的速度Fig.6 Beam velocity of underwater wet TIG arc

此外与空气焊接相比，水下湿法焊接需要承受更大的外部压力，因此电极之间需要更大的电压和电流来保证电弧的稳定燃烧，这会导致更高电弧能量和电流密度。在这种条件下，考虑电弧本身所生成的磁场将对电子束轨迹产生很大影响，生成的磁场与带电离子束的关系如式（7）所示。

式中 I为电流；dl为电流方向的微分单元；μ0为磁性常数；为单位位移向量；r为所计算的场内单元和点之间的距离。因此，Boxman等假设电介质放电过程中的电弧为：当电弧燃烧时会导致电弧收缩，特别是在水下焊接过程中，电弧自身的磁场对电弧电子束轨迹有很大影响[10]。

水下TIG焊接电子束在电弧自身磁场作用下的轨迹如图7所示，相应的速度图如图8所示。由图6、图7可知，Boxman等人的假设与仿真一致，电子束的轨迹具有显著的收缩，弧形为“铃形”。

图7 电子束自身磁场下的粒子束轨迹Fig.7 Beam trajectory with self magnetic field

图8 电子束自身磁场下的速度图Fig.8 Beam velocity with self magnetic field

5 结论

（1）在建立水下湿法焊接模型过程中，将水下介质分为电离气泡、过渡层和液体层，并分别设置相应层的相对介质常数和电导率。由此得出电子束运动轨迹及其电子束速度图。

（2）考虑到水下湿法焊接在高压环境过程中常伴随着高能量和高电流密度的影响，仿真得出高压水下湿法焊接中电弧受自身生成磁场影响，形状为“铃形”。