高慧明老师讲数学(1)
——以导数综合运用为主的压轴选择题
2019-09-27北京市第十二中学
■北京市第十二中学
从高中数学内容来看,利用导数研究可导函数的单调性,求可导函数的极值和最值,以及用导数解决实际应用题是导数在中学数学中的主要应用。从高考数学试题来看,高考对导数的考查加强了试题的综合性和应用性,由此可见,导数成了解题中必不可少的工具,所以导数的应用也成为久考不衰的考点。
类型一、利用导数的几何意义处理切线问题
例1 已知k,b∈R,设直线l:y=k x+b是曲线y=ex+x的一条切线,则( )。
A.k<1且b≤1 B.k<1且b≥1
C.k>1且b≤1 D.k>1且b≥1
解析:曲线y=ex+x的导数为y'=ex+1>1,得k>1;直线l:y=k x+b在y轴上的截距为b,对于曲线y=ex+x,当x=0时,y=1,可以知道b≤1。故选C。
评注:利用导数处理切线问题,注意三个条件的运用:设切点M(x0,y0),则切线斜率为k=f'(x0),切点坐标满足切线方程。但值得注意的是“曲线过某点的切线方程”与“该曲线在某点处的切线方程”是有区别的。
相关链接1.已知直线2x-y+1=0与曲线y=aex+x相切(其中e为自然对数的底数),则实数a的值是( )。
A.e B.2 e C.1 D.2
解析:对y=aex+x求导可得y'=aex+1,则切线的斜率令可得则函数在点处的切线方程为,整理得,结合题中所给的切线,所以a=1。
类型二、利用导数研究函数的单调性
例2 若函数在区间上单调递减,则实数a的取值范围是( )。
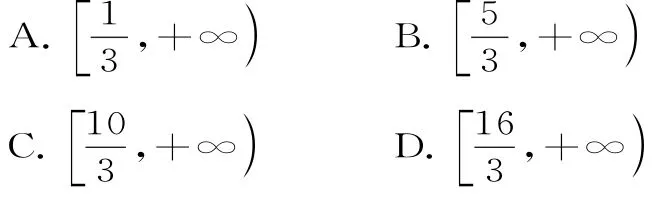
解析:因为f'(x)=x2-a x+1,由题设知x2-a x+1≤0在上恒成立,故解得
评注:恒成立问题的两种常见解题思路:①参变分离;②构造函数。由导数在单调性上的应用知,已知条件可转化为f'(x)≤0恒成立,经过参变分离转化为求函数的最值问题。
相关链接2.已知函数f(x)=ex+e2-x,若关于x的不等式[f(x)]2-a f(x)≤0恰有3个整数解,则实数a的最小值为( )。

解析:因为f(x)=ex+e2-x>0,所以[f(x)]2-a f(x)≤0,等价于f(x)-a≤0,即f(x)-a≤0恰有3个整数解,即f(x)≤a有3个整数解。因为=2 e,当a=1时,不等式无解;当a=2 e时,不等式只有一个整数解1,排除选项A,B。当a=e2+1时,由f'(x)<0可得f(x)在(-∞,1)上递减,由f'(x)>0可得f(x)在(1,+∞)上递增,f(0)=e2+1≤a,x=0合题意;x<0时,f(x)>a,不等式无解;f(1)=2 e<a,x=1合题意;f(2)=e2+1≤a,x=2合题意,当x>2时,f(x)>a,不等式无解。故a=e2+1时,有且只有3个整数解。又因为,所以a的最小值为e2+1。
类型三、利用导数求函数的极值和最值
例3 若函数-alnx存在唯一的极值,且此极值不小于1,则a的取值范围为( )。
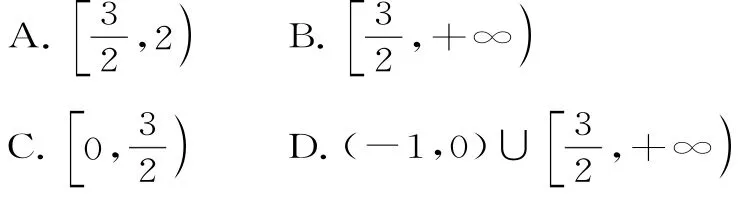
解析:对函数求导得到f'(x)=x-1+,因为函数存在唯一极值,所以导函数存在唯一的零点,且零点大于0,故得到x=1是唯一的极值,此时
评注:(1)利用导数求函数的极值,先求f'(x)=0的根x0,再和函数的定义域比较,如果落在定义域外或者落在定义域端点,此时函数单调,无极值;当落在定义域内时,将定义域分段,分别考虑x0两侧导数是否异号,从而判断是否有极值。(2)利用导数求函数的最值,先求f'(x)=0的根x0,如果落在定义域外或者落在定义域端点,此时函数单调,利用单调性求最值;当落在定义域内时,将定义域分段,分别考虑x0两侧导数是否异号,从而判断函数的大致图像,进而来求最值。
相关链接3.若实数a满足方程lnx+x-2=0,实数b满足方程ex+x-2=0,则函数的极值之和为( )。
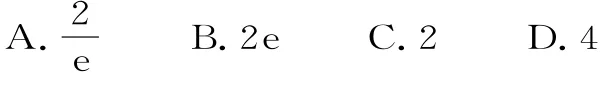
解析:依题意,a是与y=2-x交点的横坐标,b是y=ex与y=2-x交点的横坐标,因y=lnx与y=ex互为反函数,故图像关于y=x对称,由解得x=y=1,故a+b=2。由于y=xln|x|为奇函数,故极值点关于原点对称。当x>0时令,解得极值为;当x<0时,同理求得极值为a+b。故两个极值之和为2(a+b)=2×2=4。
归纳领悟:
1.与导数几何意义有关问题的常见类型及解题策略。
(1)已知切点求切线方程:①求出函数y=f(x)在点x=x0处的导数,即曲线y=f(x)在点P(x0,f(x0))处切线的斜率;②由点斜式求得切线方程为y-y0=f'(x0)·(x-x0)。
(2)已知斜率求切点:已知斜率k,求切点(x1,f(x1)),即解方程f'(x1)=k。
(3)求切线倾斜角的取值范围:先求导数的取值范围,即确定切线斜率的取值范围,然后利用函数的单调性解决。
2.求解或讨论函数单调性问题的解题策略。
讨论函数的单调性其实就是讨论不等式的解集的情况。大多数情况下,这类问题可以归结为一个含有参数的一元二次不等式的解集的讨论:
(1)在能够通过因式分解求出不等式对应方程的根时,依据根的大小进行分类讨论。
(2)在不能通过因式分解求出根的情况时,根据不等式对应方程的判别式进行分类讨论(讨论函数的单调性是在函数的定义域内进行的,千万不要忽视定义域的限制)。
3.利用导数研究函数极值、最值的方法。
(1)若求极值,则先求方程f'(x)=0的根,再检查f'(x)在方程根的左右两侧函数值的符号。
(2)若已知极值大小或存在情况,则转化为已知方程f'(x)=0根的大小或存在情况来求解。
(3)求函数f(x)在闭区间[a,b]上的最值时,在得到极值的基础上,结合区间端点的函数值f(a),f(b),然后与f(x)的各极值进行比较得到函数的最值。
