集合易错题归类剖析

■河南省太康县第一高级中学

集合是高考的必考知识点,往往在第一题的位置,从内容上看,主要以考查概念和计算为主,考查集合的交、并、补运算;从题型上看,往往以选择题、填空题的形式出现,常与不等式、函数等知识交汇考查,解决此类问题时首先要明确集合中的元素,理解基本概念、基本运算,可以借助数轴或者V e n n图直观理解。

关于该部分知识,同学们的易错点主要有:①容易忽视空集的情况;②集合的表示方法,如不等式的解集必须用集合或者区间表示,不能用不等式比表示。

例1 设集合A={x|a x2-a x+1＜0},若A=∅,则实数a的取值集合是( )。

易错分析：此题容易忽视a=0的情况,题目中并没有说是一元二次不等式。

解：当a=0时,A=∅;

综上所述,a的取值范围为[0,4]。故选D。

例2 已知集合M=,则( )。

易错分析：不会化简,感觉无从下手,找不到两个集合之间的联系与区别导致出错。

解：集合

因为k+2(k∈Z)为整数,而2k+1(k∈Z)为奇数,所以集合M、N的关系为N⊂M。故选C。

例3 已知集合A={x|log2x＞1},B={x|x2-4x-5≤0},则B∩∁RA=( )。

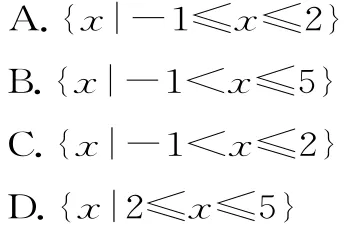
易错分析：在解决不等式与集合的交、并、补集运算的时候,区间的开闭是学生最容易出错的地方,一定要注意端点值的取舍。

解：A={x|log2x＞1}={x|x＞2},B={x|x2-4x-5≤0}={x|-1≤x≤5},则∁RA={x|x≤2},B∩∁RA={x|-1≤x≤2}。故选A。

例4 设集合A={x2-3x+2=0},B={x2-a x+2=0},若A∪B=A,求由a的值组成的集合。

易错分析：解答本题的常见错误是:①未能通过检验剔除a=±2 2;②遗漏B=∅的情况,应注意解题时空集优先的原则。

解：由A∪B=A,可知B⊆A,而A={1,2},故B可为{1,2},{1},{2},∅。

当B={1,2}=A时,显然有a=3。

当B={1},{2},或者∅时,方程x2-a x+2=0有等根,或者无实根,故Δ≤0,即a2-8≤0。解得

故所求a值的集合为