集合创新题追根溯源

■河南省太康县第一高级中学

编者提醒：河南省太康县第一高级中学是全国中学名校,本刊本期特约该校的多位一线名师,详细讲解集合、函数、导数、微积分专题的考点、题型,精心命制核心考点演练试卷,盼读者认真读一读,练一练,能收获满满哟!

集合是高中数学首先接触的内容,也是高考中的必考内容。集合是一个基本的数学概念,集合看似是非常简单的数学问题,但是其中也需要一定的数学基础,尤其是函数方面的数学基础。集合有人理解为一堆数字的集合,但是集合中的内容也被称为元素,是需要数学思想进行划分的。近几年,与集合有关的创新问题已成为高考的热点。此类题目以考查学生的探究能力和创新能力为目的,它要求考生在新的情景中使用已知的数学知识去分析问题、解决问题。本文精选近几年高考中以集合为背景的创新题型并解析,以供参考。

关于集合知识的新定义型信息题是试题改革的一个亮点,它能有效地考查学生独立获取信息、加工信息及继续学习的能力。基于此,笔者在数学学习的基础上,对高中数学中集合的子集个数创新题进行全面的分析和创新性探究。

例1 已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则集合A中的元素个数为( )。

A.9 B.8 C.5 D.4

分析：分别令x=-1,0,1,进行求解即可。

解法一：当x=-1时,y2≤2,得y=-1,0,1;

当x=0时,y2≤3,得y=-1,0,1;

当x=1时,y2≤2,得y=-1,0,1。

所以集合A中的元素有

解法二：根据集合A的元素特征及圆的方程在坐标系中的图形,如图1所示,易知在圆x2+y2=3中有9个整点,即集合A中的元素个数为9个。

点评：本题主要考查集合元素个数的判断,利用分类讨论思想是解决本题的关键。

解题方法点拨：(1)按照子集包含元素个数从少到多排列。(2)注意观察两个集合的公共元素,以及各自的特殊元素。(3)可以利用集合的特征性质来判断两个集合之间的关系。(4)有时借助数轴、平面直角坐标系、韦恩图等数形结合方法。

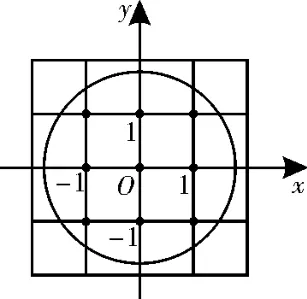
图1

例2 已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,都存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M为“垂直对点集”。给出下列四个集合:①;②M={(x,y)|y=log2x};③M={(x,y)|y=ex-2};④M={(x,y)|y=sinx+1}。其中是“垂直对点集”的序号是____。

解析：由题意得,若集合M是“垂直对点集”,则设集合内的任意一点与原点的连线为l1,则过原点与直线l1垂直的直线l2与集合M有交点。

对于①,点(1,1)∈M=,此时直线l1的方程为y=x,则直线l2的方程为y=-x,易知y=-x与没有交点,所以集合M=不是“垂直对点集”;

对于②,点(1,0)∈M={(x,y)|y=log2x},此时直线l1的方程为y=0,则直线l2的方程为x=0,易知x=0和y=log2x没有交点,所以集合M={(x,y)|y=log2x}不是“垂直对点集”;

对于③,在平面直角坐标系内画出函数y=ex-2的图像,如图2所示,由图易得,任意过原点且相互垂直的两条直线都与函数y=ex-2的图像相交,所以集合M={(x,y)y=ex-2}是“垂直对点集”;

综上所述,其中是“垂直对点集”的序号是③④。

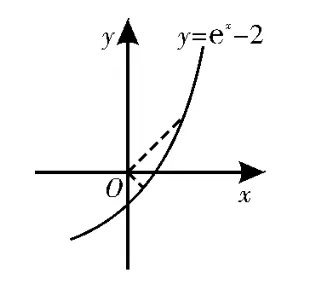
图2

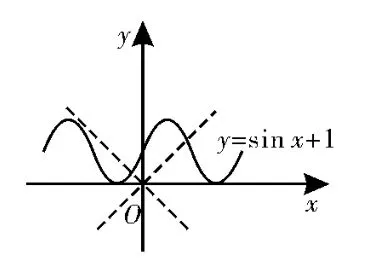
图3

跟踪训练：

1.若一个集合是另一个集合的子集,称两个集合构成“全食”;若两个集合有公共元素,但互不为对方子集,则称两个集合构成“偏食”。对于集合,若两个集合构成“全食”或“偏食”,则a的值为____。

分析：讨论a=0和a＞0,求得集合B,再由新定义得到a的方程,解出a的值即可。

解：集合1,a≥0}。

若a=0,则B=∅,即有B⊆A;

若a＞0,可得,解得a=1;

若A,B两个集合有公共元素,但互不为对方子集,可得,解得a=4。

综上可得,a=0或1或4。

点评：本题考查集合的运算及包含关系,考查同学们对新定义的理解和运用能力,运用分类讨论思想方法是解题的关键,属于中档题。

2.对于给定的非空集合A,定义集合A+={|x+y||x∈A,y∈A},A-={|x-y||x∈A,y∈A},若A+∩A-=∅,则称集合A满足性质P。

(1)判断下列集合是否满足性质P,并说明理由。

①S={3,4};②T={0,1,7}。

(2)集合A={1,2,a}⊆N,满足性质P,求a的最小值。

(3)若非空集合A⊆{x|x∈N,0≤x≤100},且集合A满足性质P,求集合A中元素个数的最大值。

分析：第一问利用新概念检验所给集合是否满足性质P,后两问则是在满足性质P的前提下,探究条件,较好地运用了归纳、分析的解题思想。

解：(1)①由S={3,4},可知S+={6,7,8},S-={0,1},此时,S+∩S-=∅,故S满足性质P。

②由T={0,1,7},可知T+={0,1,2,7,8,1 4},T-={0,1,6,7},此时T+∩T-={0,1,7}≠∅,故T不满足性质P。

(2)由A={1,2,a},可知A+={2,3,4,a+1,a+2,2a},A-={0,1,a-2,a-1},欲使A+∩A-=∅,须使a-2＞4,即a＞6,故a的最小值为7。

(3)设A={m,m+1,m+2,…,100},m∈N,则A+={2m,2m+1,2m+2,…,2 0 0},A-={0,1,2,…,100-m},欲使A+∩A-=∅,须使100-m＜2m,即,故m的最小值为3 4,此时,A中元素个数最多,为100-3 3=6 7(个)。

点评：本题考查的知识点是对新定义的理解和运用,正确理解集合A+,A-的定义是解题的关键。

解题方法点拨：求集合中元素个数的最大(小)值问题的方法通常有:类分法、构造法、反证法、一般问题特殊化、特殊问题一般化等。需要注意的是,有时一道题需要综合运用几种方法才能解决。