创新题型这样考

赵爱丽

类型一：设置“新定义”

“新定义”试题是指给出一个考生从未接触过的新规定、新概念，要求考生现学现用，其目的是考查考生的阅读理解能力、应变能力和创新能力，培养学生自主学习、主动探究的品质.此类型问题可能以文字的形式出现，也可能以数学符号或数学表达式的形式出现，要求考生要先准确理解“新定义”的特点，再加以灵活运用。特别提醒：“给什么，用什么”是运用“新定义”解题的基本思路。

例1.(2018 届河南郑州一模)如果把四个面都是直角三角形的四面体称为“三节棍体”，那么从长方体八个顶点中任取四个顶点，则这四个顶点是“三节棍体”的四个顶点的概率为_____.

解析：从长方体ABCD-A1B1C1D1中任选四个顶点的选法有(种)，以A为其中一个顶点的四个面都是直角三角形的三棱锥有A-A1D1C1，A-A1B1C1，A-BB1C1，A-BCC1，A-DCC1，A-DD1C1，共6 个。

同理，以B，C，D，A1，B1，C1，D1为其中一个顶点的三棱锥也各有6 个，但所有列举的三棱锥均出现2 次，所以四个面都是直角三角形的三棱锥有。

点评：本题以立体几何知识为背景，考查古典概型概率计算公式，形式较为新颖。有利于考查考生的阅读能力、审题能力和综合应用能力，其求解关键是正确理解新定义“三节棍体”，并根据长方体的对称性，利用列举法求解长方体中“三节棍体”的个数。

类型二：设置“新运算”

“新运算”是指在现有的运算法则和运算律的基础上定义的一种新的运算，是一种特别设计的计算形式，它使用一些特殊的运算符号，如“*”“⊗”“※”等，这些符号与四则运算中的加减乘除符号是不一样的。“新运算”类问题的情境一般比较陌生，求解时考生需要坦然面对，先准确理解“新运算”法则，再加以灵活运用即可解决问题。特别注意：新定义的算式在没有转化前，是不适合运用现有的运算法则和运算律进行计算的。

例2.定义一种运算“※”，对于任意n∈N*均满足以下运算性质：(1)2※2017=1；(2)(2n+2) ※2017=(2n)※2017+3.则2018※2017=_______.

解析：设an=(2n)※2017，则由运算性质(1)知a1=1，由运算性质(2)知an+1=an+3，即an+1-an=3.

于是，数列{an}是等差数列，且首项为1，公差为3.

故2018※2017=(2×1009)※2017=a1009=1+1008×3＝3025.

点评：注意到(2n) ※2017 与

[2(n+1)]※2017((2n+2) ※ 2017)结构相同，具体区别为前边是“n”，后边是“n+1”，于是，可将它们看作某一数列的相邻两项，从而通过“换元”将不熟悉的“新运算”问题转化为熟悉的等差数列问题，这是求解本题的关键。

类型三：设置“新考查方向”

“新考查方向”试题是指试题考查的方式、方法与常规试题不同，此类试题设计新颖，注重对所学数学知识、方法的有效整合，侧重考查考生的综合运用能力。此类型问题的设置充分体现了考纲要求——对数学基础知识的考查，注重学科的内在联系和知识的综合性，在知识网络的交汇点处设计试题，使对数学基础知识的考查达到必要的深度；对数学能力的考查，强调“以能力立意”，侧重体现对知识的理解和应用，尤其是综合和灵活的应用，以此来检测考生将知识迁移到不同情境中的能力，从而检测出考生的理性思维的广度和深度以及进一步学习的潜能。

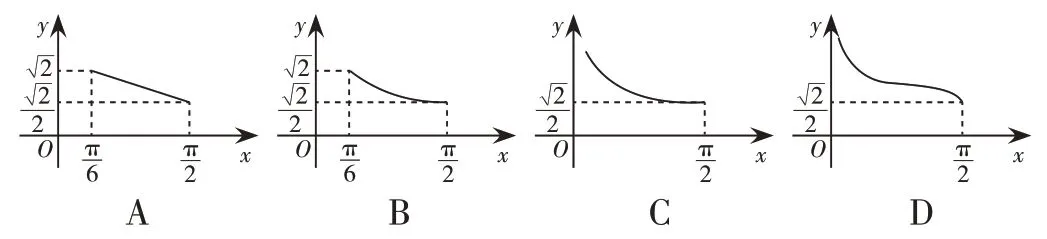
例3.已知三棱锥O-ABC，OA，OB，OC两两垂直，且OA=OB=，OC＝1，P是△ABC内任意一点，设OP与平面ABC所成的角为x，OP=Y，则Y关于x的函数的图像为( )

解析：设点O在平面ABC内的射影为O′，连接OO′，OP，O′P，根据等体积思想得.

因为∠OO′P=，所以OP=，即y=.易知当点P在点A或点B位置时，x取得最小值，排除选项C，D.又在上，函数y=单调递减且其图像为光滑曲线，所以排除选项A，选B。

点评：本题是立体几何中线面角与函数图像的综合试题，形式新颖，解题的关键是先根据等体积思想得到函数关系式，再灵活利用函数性质排除错误选项。

创新型数学问题从形式上看很“新”，其提供的观察材料和需要思考的问题异于常规试题，需要考生具有灵活、创新的思维能力，善于进行发散性、求异性思考，寻找对材料内涵的解释和解决问题的办法。此类问题考查的内容都在考纲要求的范围之内，即使再新，也是在考生“力所能及”的范围内。只要拥有扎实的数学基础知识，以良好的心态坦然面对新情境，便可轻松破解。