大中衔接从北京物理高考24题谈空气阻力
2019-09-26胡继超
胡继超 陈 曦
(中国人民大学附属中学,北京 100080)
北京市高考物理试卷近年积极创新,将微观与宏观的结合,鼓励同学利用所学物理知识解决生活问题,今年北京市高考物理第24题就是一道非常有趣的问题。题目内容如下:
雨滴落到地面的速度通常仅为几米每秒,这与雨滴下落过程中受到空气阻力有关。雨滴间无相互作用且雨滴质量不变,重力加速度为g。
(1) 质量为m的雨滴由静止开始,下落高度h时速度为u,求这一过程中克服空气阻力所做的功W。
(2) 将雨滴看作半径为r的球体,设其竖直落向地面的过程中所受空气阻力f=kr2v2,其中v是雨滴的速度,k是比例系数。
a. 设雨滴的密度为ρ,推导雨滴下落趋近的最大速度vm与半径r的关系式;

b. 示意图中画出了半径为r1、r2(r1>r2)的雨滴在空气中无初速下落的v-t图线,其中________对应半径为r1的雨滴(选填①、②);若不计空气阻力,请在图中画出雨滴无初速下落的v-t图线。
(3) 由于大量气体分子在各方向运动的几率相等,其对静止雨滴的作用力为零。将雨滴简化为垂直于运动方向面积为S的圆盘,证明:圆盘以速度v下落时受到的空气阻力f∝v2(提示:设单位体积内空气分子数为n,空气分子质量为m0)。
标准解答如下:
(1) 根据动能定理
可得
(2) a. 根据牛顿第二定律
mg-f=ma
得
当加速度为零时,雨滴趋近于最大速度vm,雨滴质量
由a=0,可得,雨滴最大速度
b. ①
如答图2。
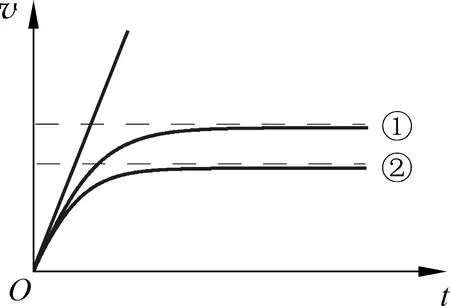
答图2
(3) 根据题设条件:大量气体分子在各方向运动的几率相等,其对静止雨滴的作用力为零。以下只考虑雨滴下落的定向运动。
简化的圆盘模型如答图3。设空气分子与圆盘碰撞前后相对速度大小不变。在Δt时间内,与圆盘碰撞的空气分子质量为
Δm=SvΔtnm0
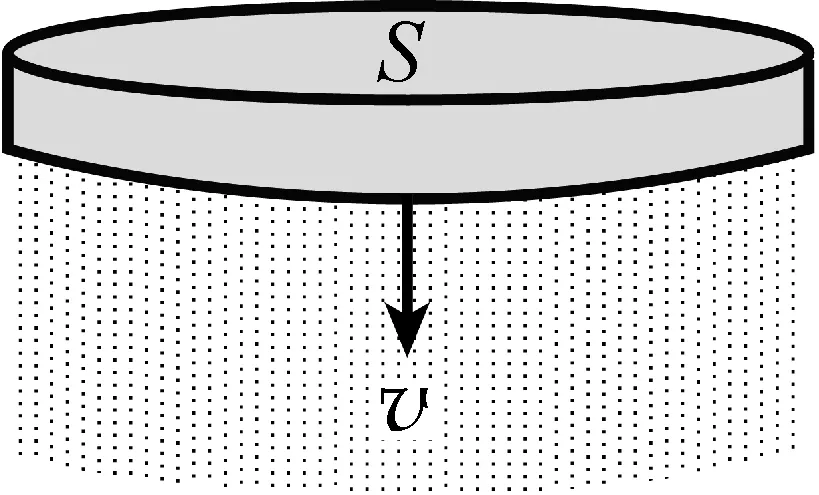
答图3
以F表示圆盘对气体分子的作用力,根据动量定理,有
FΔt∝Δm×v
得
F∝nm0Sv2
由牛顿第三定律,可知圆盘所受空气阻力
f∝v2
采用不同的碰撞模型,也可得到相同结论。
一道好题,总是会激发同学们的思考,此题解罢,自然会有好奇心强的同学提出疑问,空气阻力大小究竟和速度的二次方成正比还是与速度的一次方成正比。
物体所受的空气阻力通常由3部分构成,第一是气流撞击物体所产生的阻力,也就是本题让我们求解的部分;第二是摩擦阻力,通常情况,车辆即使高速行驶,气流与车身的摩擦阻力也基本可以忽略不计;第三则是外形阻力,当物体向前运动的时候,会在后面形成一个真空区,从而导致周围气体分子加速运动,这部分阻力与气体的黏滞系数、雷诺数以及外形(空气阻力系数)有关,在高速运动中,这部分阻力占有主要作用。
这里我们先考虑对于雨滴这样的低速运动物体来说,如何利用碰撞模型计算圆盘形雨滴下落时,气流撞击产生的空气阻力。
在碰撞模型中,应该把气体分为两部分,一部分是圆盘下方的气体,一部分是圆盘上方的气体,当圆盘以速度V下落时,被圆盘上方和下方的气体分子同时碰撞,产生的作用力之差为圆盘受到的由碰撞产生的空气阻力。因为气体分子热运动的不规则性,同时与圆盘碰撞的气体分子有不同的速度大小与速度方向。

图1
如果气体稀薄(气体分子的自由程大,与圆盘碰撞后的气体分子不会碰撞周围其它分子),且圆盘的速度缓慢,我们可以认为圆盘的运动并不改变气体中分子按照速度分布的函数。取竖直向下建立z轴,此时,我们可以设在圆盘的下侧,竖直向上分速度为vz i的气体分子有ni个,则在Δt时间内,在圆盘的下表面以该vz i分速度与圆盘碰撞的气体分子位于一个以S为底,以(V+vz i)Δt为高的圆柱体内, 其数目为Ni=niS(V+vz i)Δt。这些气体分子在z轴方向上相对圆盘的初速度为V+vz i,碰撞后对圆盘的速度大小也为V+vz i,故气体分子对地的速度大小为2V+vz i,若气体分子质量为m,其动量变化量Δp=m(2V+vz i-(-vz i))=2m(V+vz i)。
由动量定理可知,圆盘给这部分气体分子的作用力
在圆盘速度很低时,可以认为圆盘上方竖直方向分速度竖直向下的气体分子也会都撞击到圆盘上,并产生大小为
f上i=2mniS(vz i-V)2
的作用力,则两个作用力之和为
由牛顿第三定律可知,以竖直方向分速度大小vz i运动的粒子对圆盘的作用力大小也为8mniSVvz i,方向竖直向上。
对不同vz运动的粒子与圆盘的作用力求和,可得圆盘所受的空气撞击产生的阻力
虽然高中生并不知道ni的具体分布函数(麦克斯韦分布律),但显然这个阻力与圆盘下落速度的一次方成正比。
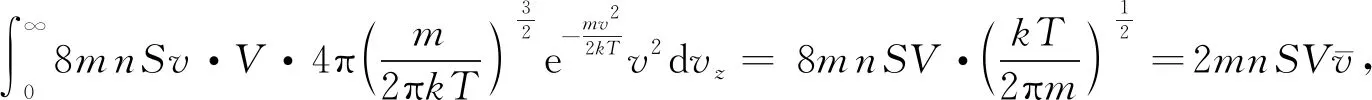
该结论适用于圆盘速度非常小的情况,此时可以认为圆盘上方所有向下运动的气体分子都可以撞到圆盘,而圆盘下方所有向下运动的气体分子都不会撞到圆盘。
若圆盘的速度较大时,在考虑气体分子碰撞产生的阻力时,在圆盘上方向下运动的分速度小于圆盘速度V的气体分子就不能撞到圆盘上,而在圆盘下方则会多出来竖直向下分速度小于V的气体分子对圆盘的撞击。此时就要调整两个作用力的积分区间,当V远大于气体分子热运动速率时,可以认为圆盘上方的气体分子几乎都不能与圆盘发生碰撞,此时的圆盘所受的碰撞产生的作用力
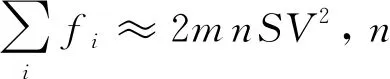
对北京市这道高考题来说,如果让考生在高中范围内推导气体阻力与速度平方成正比,题设更准确的表达应为“将雨滴简化为垂直于运动方向面积为S的圆盘,当圆盘下落速度远大于气体分子热运动速度时(实际下落时达不到这么大速度),气体分子的热运动可以忽略不计,请在此条件下证明:圆盘以速度v下落时受到的空气阻力f∝v2。”至于题目提到的“由于大量气体分子在各方向运动的几率相等,其对静止雨滴的作用力为零。”这个结论当圆盘一开始运动后就已经不再成立了。

首先从数学上来考察f=k1+k22的意义。圆球受到的阻力应该是圆球速度的函数,即f=f()。圆球静止时不受阻力,即f(0)=0。在v=0附近对f=f()做泰勒展开,忽略三阶以上的量得到f=k1+k22。当圆球的速度足够小时k1≫k22,阻力满足f≈k1。当圆球速度足够大时k1≪k22,阻力满足f≈k22。
接下来考察f=k1+k22的物理意义。根据《流体力学》,当圆球的速度足够小时,圆球周围流体的流动满足斯托克斯流动模式,压强均匀分布。流体流过圆球时受到的压力平衡,圆球前、后方流体的宏观流动速度相同。此时流体对圆球的黏性起主导作用,导致f≈k1。这和碰撞模型的结论是一致的。当圆球的速度足够大时,圆球周围流体的流动满足奥辛流动模式,压强分布不均匀。流体流过圆球时,圆球前、后方的压强差使流体流动的速度加快。此时圆球的动量转化为流体宏观流动的动量,导致f≈k22。这和流体模型的结论是一致的。所以说流体模型和碰撞模型都只在特定条件下成立。
(1) 将雨滴近似为面积为S的圆盘,运动方向和圆盘垂直。
(2) 所有空气分子无规则热运动速度的方向都和雨滴速度方向平行。
(3) 单位体积内分子数为n。雨滴前方一半空气分子的热运动速度与雨滴速度同向,另一半空气分子的热运动速度与雨滴速度相反。雨滴后方的空气分子亦然。
(4) 雨滴以速度v下落时挤压其前方的空气,使得这些空气的宏观流动速度为vf (5)vf是v的函数,即vf=vf(v)。雨滴静止时,雨滴前方的空气也静止,即vf(0)=0。当雨滴速度不是特别大时,可以近似认为vf=vf(v)=kfv,0 (6) 同理,近似认为雨滴后方的空气的宏观流动速度雨滴运动方向相同,且满足vb=vb(v)=kbv,0 (7) 以空气为参考系,所有分子热运动速度的大小都等于u。则地面参考系中,空气分子的速度如图2所示。 (8) 空气分子热运动的速度u远大于空气宏观流动速度vf、vb和雨滴的运动速度v。所以只有向着雨滴运动的空气分子才能和雨滴发生碰撞。 上述假设可以总结为图2所示模型。以圆盘为参考系,雨滴前方向着雨滴运动的分子速度大小为u+(1-kf)v,Δt时间内与圆盘碰撞的空气分子质量为 Δm=Snm0[u+(1-kf)v]Δt 图2 与雨滴弹性碰撞后这些分子的速度反向。根据动量定理,圆盘受到的向后的力为 同理圆盘后方分子碰撞圆盘产生的向前的力为 f2=2Snm0[u-(1-kb)v]2 所以圆盘所受合力为 其中k1=4Snm0(2-kf-kb)u,k2=2Snm0·[(1-kf)2-(1-kb)2]。这样我们就得到了气体阻力的一般表达式。下面简单讨论f=k1+k22的物理意义。首先0 本文中,我们从热学和流体力学的角度出发,讨论了雨滴下落过程中所受阻力的表达式。分析表明,当雨滴的速度足够小时k1≫k22,空气对雨滴的黏性起主导作用,阻力满足f≈k1。当雨滴速度足够大时k1≪k22,雨滴的动量转化为空气宏观流动的动量,阻力满足f≈k22。在此基础上我们修正了空气阻力的碰撞模型,推导出空气阻力的定性表达式f=k1+k22。