军队院校大学物理教学突出“军味”的案例剖析

刘协权 倪新华

(陆军步兵学院基础部，江西 南昌 330103)

大学物理作为一门科学文化类通用基础课有着悠久的历史，自伽利略用科学的方法研究自然界的物理现象为开端，物理学已经历了400多年的发展演变历程，从牛顿力学、热学、电磁学、光学到相对论、量子力学已经形成了比较完备的科学体系。军队院校的大学物理教学必须坚决贯彻执行习近平“面向战场、面向部队、面向未来”的指示精神，同时也应该遵循教育教学的规律，在保持大学物理课程体系相对完整的基础上，突出大学物理与军事应用的融合，让军队院校的大学物理课程渗透“军味”，为此，中央军委训练管理部组织制定的军队院校大学物理教学大纲对军事应用部分也提出了明确要求。笔者认为，深入研究学员未来任职岗位需求，将军事应用案例自然融入到大学物理的教学内容之中，是实现为战教战向实战聚焦的一条好途径。

学员步入大学在开始学习大学物理时存在两个认识上的误区，一是认为大学物理就是对中学物理的简单重复，炒剩饭没味道；二是认为军校学员只要军事上过硬就可以了，至于科学文化课的学习有了中学的基础就够了，大学物理可能没什么用。因此在大学物理教学之初，就有必要采取措施让学员认识到学习大学物理的重要性，此时空喊口号没用，通过鲜活生动的案例才能让学员心服口服，从而激发学员自觉学习科学文化知识，为未来成为一名合格的军人奠定理论基础。笔者选择了大学物理开篇力学部分的4个教学案例与同行共同剖析。

1 炮手炮击敌堡

例1：我方一个小分队正在攻击前进，发现前方水平距离s=3000m处，在高度h=500m的山坡上有一个敌人的防御工事，现欲用携行的迫击炮将其击毁，不考虑空气阻力，试计算我方迫击炮的初速至少要为多少？若已知火炮的初速度为v0=300m·s-1，试确定火炮的射角应为多少？

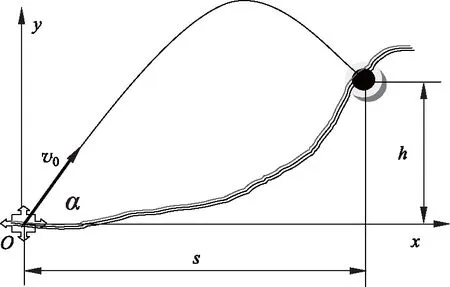
图1 炮手炮击敌堡示意图

解：见图1，设火炮射击的初速度为v0，射角为α，则弹丸飞行的运动方程为

消去参数t可得轨迹方程：

以上的求解过程是中学的传统套路，多数学员可以掌握，但是接下来该如何处理，就会陷入迷茫，无从下手。

为了便于确定射角，将上式改写为

要能击中目标，则需满足x=s时，y=h，代入上式整理可得：

求解该关于tanα的二次方程可得：

(1)

要想击中目标，即上述关于射角α的方程有解，则需要满足以下条件：

(2)

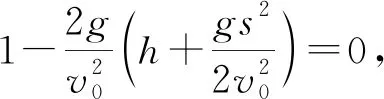
(3)

若已知火炮的初速度为v0=300m·s-1，并且由于时间紧迫不允许加、减装药。直接将v0=300m·s-1代入方程(1)可得应选的射角为：α1=80.2°，α2=19.4°。

从实战考虑，到底是该选择大射角还是选择小射角也是值得斟酌的。一般而言敌方工事的正面防护较强，而顶部较弱，因此采用大射角从顶部吊射效果更佳，另外对于迫击炮射击而言，通常也要求射角α>45°。

2 巷战投掷手雷

例2：在巷战中，发现某建筑物背后有一股敌人，建筑物的结构尺寸如图2所示，我方欲投掷手雷消灭敌人。假设投掷手雷的出手高度为1.6m，试计算投弹手应该站在建筑物前什么位置以什么样的角度抛掷手雷需要的初速最小(最省力)？试计算该最小速度。

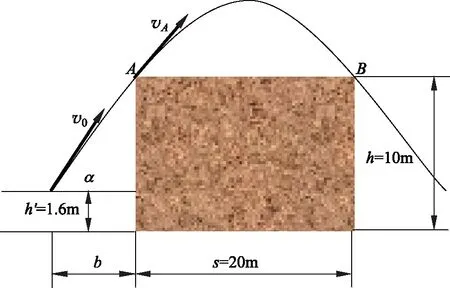
图2 某建筑物结构示意图

以往研究的问题都是平地斜抛问题，不涉及飞越障碍物的问题，但从实战出发，将手雷抛到障碍物之后是巷战很可能遇到的实际问题，利用已有知识，通过教员的讲解诱导，学员完全有能力得出正确的结果，同时也培养了学员运用所学知识解决实际问题的能力。

解：由于出手点与图2中A点的高度差是一定的，手雷自出手点到达A点的动能损失就是一定的，因此要想有最小的初速，则手雷在A点时所需速度应该为最小。

以上分析判断是解决问题的关键点，是找出突破口的钥匙。

以上这部分是中学物理学习的内容，可以指导学员自己得出结论。

设投掷手雷的初速度为v0，抛投角为α，根据动能定理可得：

在水平方向上手雷的飞行速度不变，可得：

vAcos45°=v0cosα⟹α=58.6°

设自手雷出手到运动至A点飞行时间为t，则有：

v0sinα-gt=vAsin45°⟹t=0.645s

所以站立位置到墙根的距离应为

b=v0cosα·t=6.38m

问题求解结束还可以引导学员自己估算一下，考虑到空气阻力的影响，欲想完成上述作战任务，投手需要具备在平地上投掷50m以上距离的实力。

3 跳伞极限速度

空降兵在跳伞时除了受到重力的作用外，打开降落伞时还将受到空气阻力的作用，从而降低下落的速度，保证空降兵落到地面时速度不会太大。降落伞提供的空气阻力大小可以近似地表示为F=kv，方向与速度方向相反，类似的问题还包括载人飞船回收、蛟龙号潜海等问题，其特点都是阻力是速度的函数，即F=f(v)。此类问题，学员中学没有学过，求解它既要用到物理知识，还要用到高等数学有关微分方程的知识，有一定难度。但此类问题很有实际应用价值，从为战教战出发，此问题是学员应该掌握的知识点。

例3：如图3，质量为m=60kg的空降兵自空中跳下，先做自由落体运动，3s后打开降落伞，它除受重力作用外，还受到一个与速度大小v成正比的阻力的作用，即F=kv，比例系数k为正的常数，k=200kg·s-1。试求：(1)空降兵下落过程中的最大速度vm；(2)下落后期的稳定速度v∞；(3)当速度减小到v=vm/5之前空降兵下落的总高度。

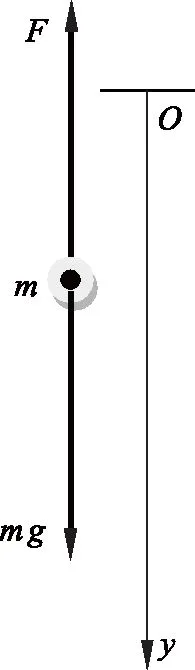
图3 伞降示意图

解：(1) 开始阶段空降兵作自由落体运动，3s末打开降落伞瞬间其下落速度将达到最大，该时段不计空气阻力，显然：vm=gt=29.4m·s-1。

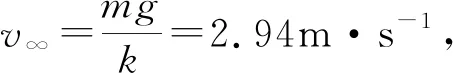
(3) 研究开伞后空降兵的运动，根据牛顿第二定律可得：

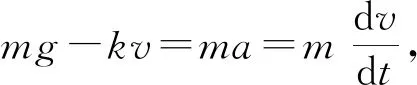
刚开伞时为计时起点，此刻v=vm=29.4m·s-1，到任意时刻t的速度为v，则可进行如下积分：

(4)

可得：

(5)

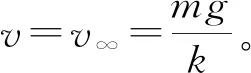
设刚开伞时的坐标为y=0，到任意时刻t时坐标为y，由式(5)可进行如下积分：

(6)

可得：

(7)

当速度减小到v=vm/5=5.88m·s-1时，此速度大体相当于从不超过2m的高处跳下落地时的速度，以该速度落地也是可以保证安全的。通过式(5)求得：

将t=0.659s代入式(4)求得这一时段空降兵下落的高度为

4 空气弹道计算

早在中学期间，学员通过中学物理的学习就知道弹丸的飞行轨迹是条抛物线，所以在大学物理讲到斜抛运动时学员就没有什么兴趣了。但是弹道是条抛物线只是忽略空气阻力情况下得到的一个理想结果，实际的弹丸飞行还将受到空气阻力的作用，为了接近实战，在军校的大学物理教学中研究弹道应该考虑空气阻力的影响。

图4 迫击炮弹道示意图

例4：如图4，弹丸质量为m，以初速度v0，射角为α发射，飞行中它除受重力作用外，还受到一个与速度v的大小成正比的黏性阻力的作用，比例系数为k，k为正的常数，即F=-k。试求弹丸的飞行轨迹。

解：本题与例3相似，但从一维问题拓展为二维问题。弹丸在飞行中的受力情况如图4所示，根据牛顿第二定律可得：

mg-k

(8)

建立直角坐标系Oxy，将式(8)分别向x轴和y轴投影可得

(9)

这是两个微分方程，需要分离变量通过积分求解，因此该问题也是一个很好的数学问题。

式(9)可以改写为

(10)

考虑初始条件可进行如下积分：

(11)

可得：

(12)

(13)

可得：

(14)

式(14)就是考虑黏性阻力时弹丸的运动方程，消去参数t可得轨迹方程：

(15)

其中，vx0=v0cosα，vy0=v0sinα，黏性阻力系数k与空气密度以及弹丸的大小和形状等因素有关，这可通过风洞实验测得，也可以通过靶场实验获得。假设某弹丸的质量m=10kg，初速度v0=282.8m·s-1，射角α=45°，黏性阻力系数k=0.5kg·s-1，可以推算出其实际射程为3209m。若不考虑空气阻力其射程将可达8160m，由此可见空气阻力对射程的影响是非常大的。

多年从事军队院校大学物理教学的实践使笔者深刻体会到：(1)大学物理虽然是中学物理的延续，但一定要让学员感受到大学物理不是炒剩饭，而是在中学物理基础上的多维度深化，要通过大学物理平台让学员站得更高，看得更远，思维能力得到升华，这样才能激发学员的探索欲望，收到良好的教学效果；(2)教育部启动了新工科研究，军队院校也正在大力开展为战教战向实战聚焦的教学改革，这些都给军队院校的大学物理教学提出了新的更高的要求，物理与军事、物理与工程的高度融合势在必行，教师要努力把军事、工程和生活中的一些鲜活案例自然融入到教学之中，让军队院校的大学物理教学 “军味”十足。

后记：本文是教育部新工科研究与实践项目“新工科重要基础课程——大学物理课程体系的构建”和陆军步兵学院教学研究课题“军队院校大学物理教学突出军味的研究与实践”的研究内容之一。