基于stribeck摩擦模型的新型制动系统的振动研究

王宇

摘要：为了深入研究制动系统，建立了三自由度盘式制动系统模型，采用了stribeck摩擦模型计算盘块之间的摩擦力。通过数值分析，研究了制动压力对制动系统动力学特性的影响规律。结果表明，随着制动压力的变化，系统出现了周期振动与混沌振动现象，制动压力的大小对制动系统动力学特性具有显著影响。

关键词：三自由度;制动系统;混沌;粘滑;振动

制动系统是车辆的一个主要系统，其性能好坏直接影响着车辆行驶的安全性和乘坐舒适性。随着汽车保有量的爆炸式增长，制动噪声也成为了城市噪声的重要组成部分，对制动系统进行研究的必要性不言而喻，因此国内外学者对制动系统的动力学特性进行了大量研究。

Mill是最早进行制动系统研究的学者之一，其早在1938年就发现了制动的粘滑振动并提出了stick-slip概念，得出制动系统的粘滑振动与摩擦参数的负斜率特性密不可分的结论[1]。为了对粘滑振动的本质进行探究，后来学者们对制动系统进行了简化，得到不同自由度的制动系统动力学模型，其中影响最深、运用最广泛的是结构简单、利于分析的质量块—传送带单自由度模型。Bowden and Leben 通过对此模型的研究分析得出了与Mill相同的结论：摩擦的负斜率特性是粘滑振动现象出现的必要条件[2]。U. Andreaus 得出了另一个重要的结论：粘滑振动现象出现与否与传送带的速度有重大关系，且驱动速度较低时容易出现粘滑现象[3]。随着研究的深入，制动系统模型得到进一步的丰富和发展。Ugo Galvanetto 在单自由度模型的基础之上通过增加一个并联的质量块将模型扩展为双自由度模型，发现了系统的复杂运动特性，重点研究了与时间相關的动力学行为[4]。D Wei， L Li等人在Ugo Galvanetto的基础上找到了低速区间内系统的多极限环[5]。Valery Pilipchuk 等人通过考虑悬架旋转自由度将质量块-传送带单自由度模型扩充为双自由度模型，并通过实验与数值分析对比找到了系统的粘滑振动，并认为传送带的绝热减速是导致系统非平稳效应的原因之一，在制动最后阶段，蠕变滑移能够导致动力学频谱的显著扩大[6]。H. Hetzler等人通过研究将制动盘的扭转振动考虑到制动系统模型之内，建立了更加符合制动系统实际运动的双自由度系统，但H. Hetzler并未对模型进行深入的分析[7-8]。D Wei 和J Ruan通过Hetzler的模型对系统的稳定性进行了分析，并认为随着车速的降低制动系统会出现分岔混沌振动现象[9]。Crowther将制动系统模型进一步扩充，建立了包括传动和车轮的四自由度系统模型，并通过该模型发现随着制动压力的改变，系统的动力学特性会发生变化，出现粘滑振动现象[10-11]。Wu建立了带有车轮和制动钳体的七自由度制动系统模型，将扭转和轴向两个自由度考虑在内，并通过分析认为制动压力产生或者释放的速率是制动噪声产生的原因之一[12]。

本文在现有的研究基础之上，考虑到摩擦块的切向、轴向自由度和制动盘的扭转自由度，建立了一个三自由度的制动系统动力学模型，并通过数值计算找到了系统的阵发性混沌，计算分析结果为制动系统参数的选择提供了理论依据。

1    三自由度制动系统动力学模型

4    结论

本文在总结前人研究工作的基础之上，建立了包含切向、轴向和扭转三个自由度的制动系统模型，通过数值计算，找到了系统的分岔与混沌现象，重点研究并分析了制动压力对制动系统动力学特性的影响，对认识非线性动力学对制动系统颤振的影响具有理论指导意义。

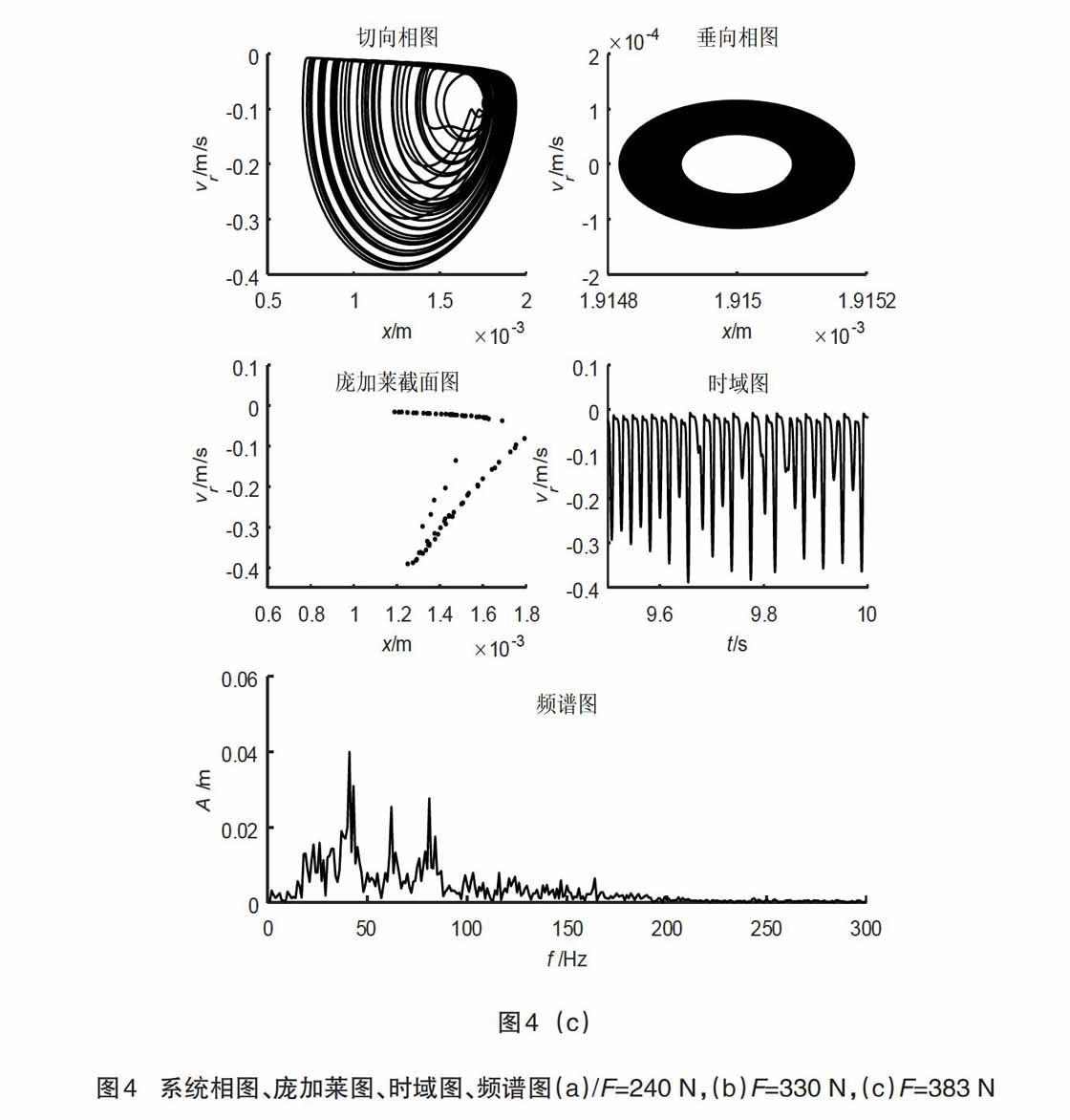
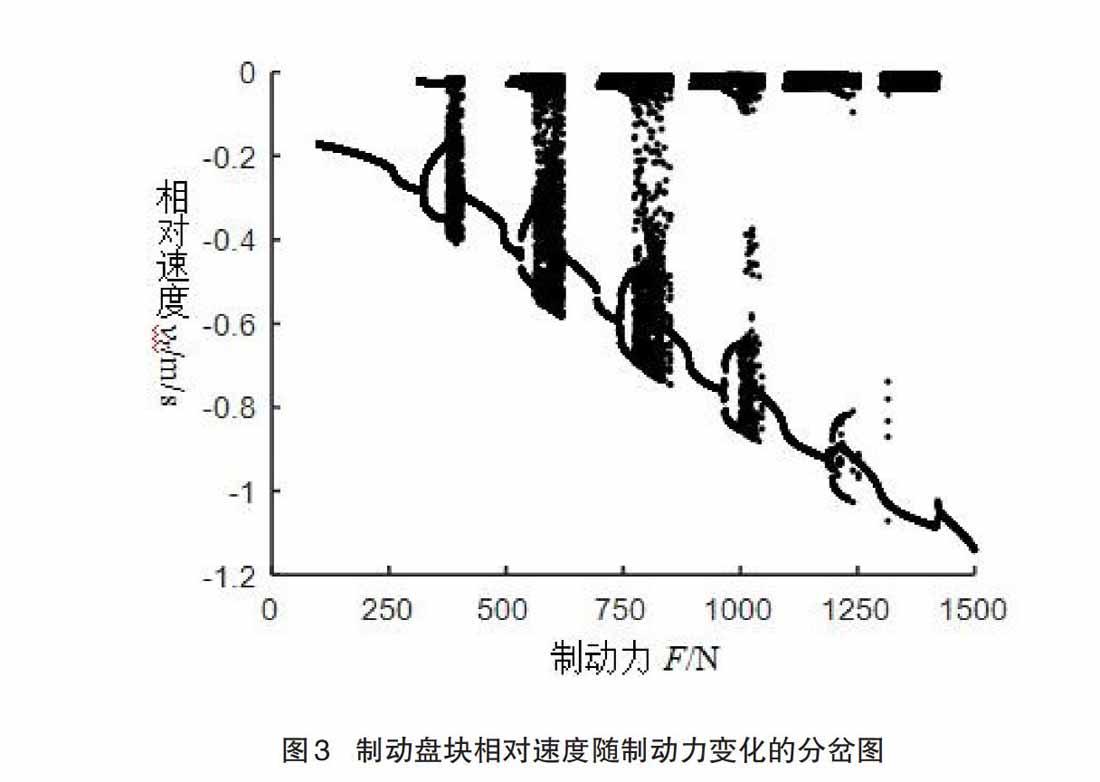
结果表明，在不考虑结构参数的情况下，随着制动压力的增长，系统交替出现周期和混沌运动，并在一定范围内周期不断减少，混沌运动逐渐增加，但是当制动压力增长到一定程度时，系统的混沌逐渐减少，直至消失，系统只进行周期振动。该发现对制动系统制动压力的匹配选择具有重要的理论指导作用。

参考文献：

[1] MILLS H R.  Brake squeak [R]. Technical Report 9000 B， Institution of Automobile Engineers， 1938.

[2] BOWDEN F P，LEBEN L. The nature of sliding and the analysis of friction [J]，Royal Society of London Proceedings Series A Mathematics Physics and Engineering Science， 1939， 169（169）： 371-391.

[3] ANDREAUS U，CASINI P.Dynamics Of Fiction Oscillators Excited by A Moving Base And/Or Driving Force[J].Journal of Sound and Vibration， 2001， 245 （4）： 685-699.

[4] GALVANETTO U， KNUDSEN C. Event Maps in a Stick-Slip System [J].Nonlinear Dynamics 1997，13（2）： 99-115.

[5] WEI D G，LI L L，SHI W，et al. Multiple limit cycles of a dual?cylinder dual?pad brake system caused by dry friction[J].Journal of Vibroengineering，2015，17（7）：3 949-3 966.

[6] PILIPCHUK V ，OLEJNIK  P ，AWREJCEWICZ b J.Transient friction-induced vibrations in a 2-DOF model of brakes[J].Journal of Sound and Vibration，2015，344：297-312.

[7] HETZLER H，SEEMANN W. Friction Modes in Low Frequency disc-brake noise - experimental results and implications on modelling [J]. Pamm， 2006， 6（1）：307-308.

[8] HETZLER H，SEEMANN W. Brake vibrations at very low driving velocities [J]. PAMM， 2004， 4（1）：87-88.

[9] WEI D G， RUAN J Y，ZHU W W，et al. Properties of stability， bifurcation， and chaos of the tangential motion disk brake[J] Journal of Sound and Vibration，2016，375：353-365.

[10] CROWTHER A R，SINGH R. Analytical investigation of stick-slip motions in coupled brake-driveline system[J]. Nonlinear Dynamics， 2007，50（3）： 463-481.

[11] CROWTHER A R， SINGH R. Identification and quantification of stick-slip induced brake groan events using experimental and analytical investigations{J]. Noise Control Engineering Journal， 2008，56（4）：235-255.

[12] WU G Q，JIN S Y. Combination of Test with Simulation Analysis of Brake Groan Phenomenon [J]. SAE Intmational Journal of Passenger Cars.DOI：10.4271/2014-01-0869.

Abstract： A three-degree-of-freedom disc brake system model is established， and the friction between the brake disk and pad is calculated by using the stribeck friction model. The influence of brake pressure on dynamic characteristics of brake system is studied by numerical analysis. The results show that， with the change of brake pressure， the system shows the phenomenon of periodic vibration and chaotic vibration， and the size of brake pressure has a significant influence on the dynamic characteristics of the braking system.

Key words： three degrees of freedom; braking system; chaos; stick-slip; vibration

責任编辑    祁秀春