基于SimVascular的腹主动脉复杂模型构建与血流动力学仿真研究

吴全玉 潘玲佼 于冬梅 范振敏 张文强 陶为戈

摘要：研究在不同入口血流速度下，仿真计算逼近人体腹主动脉和髂动脉及其分支形状的血流动力学参数的变化情况。依据获取的CT血管数据，采用开源SimVascular软件构建腹主动脉以及附近主要动脉的血管模型，具体包括腹主动脉干、腹腔动脉、脾动脉及其分支肝动脉，肠系膜上下动脉及其分支，左右髂动脉及其分支和左右肾动脉。通过Fluent进行仿真计算，主要分析人体血管各处的血流速度矢量、静态压力和剪切力的血流动力学表现。在入口处施加不同的速度载荷条件，分别定义收缩期的类抛物线函数速度和平均定值速度，发现在这两种条件下，血管在分叉和小直径血管处，都出现较大速度和剪切力。但是在肠系膜上动脉和左右髂动脉的远端出现明显的不同。同时还发现入口速度的逐渐增加，会加倍血管各分叉处的血流速度。总之，成功构建复杂血管网络并进行仿真计算，将有助于医生更深入理解动脉血流力学特征。

关键词：腹腔主要动脉系;血流动力学;血流速度;静态压力;剪切力

目前，心脑血管疾病仍然是全球人类死亡和致残的主要原因，其引发的核心在于血流的局部和区域问题[1]。 要在人体上进行直接血流参数测量，运用有创测量技术在实践中存在着各种局限性，而通过计算流体力学（computational fluid dynamics CFD）的方法，可以计算出各种血流指标，该方法已经被广泛应用到各处动脉血管的研究中[2-3]。郑河荣等[4]采用MRI断层脑血管数据，运用中国科学院自动化研究所开发的MITK平台，快速实现脑血管的3D重建，通过对脑内动脉血流的仿真，给出脑动脉血流的特征参数;Saho[5]等人采用颅内血管断层技术，结合3-D流体力学模型，分析了复杂脑动脉瘤的血流情况;陈珍[6]等研究颈内动脉狭窄时 Willis环的血液动力学特点，发现当狭窄大于50% 时，环内血液需要重新分配，只有通过提升压力才能有效增加脑部供血;Potters[7]等人构建颈内动脉及相关疾病双向流固耦合模型的血流模拟;刘莹[8]等通过颈动脉和冠状动脉内非稳态血流的数值模拟，探索颈动脉粥样斑块形成与发展机理。在腹部主动脉的研究方面学者较多，孙正[9]等人研究主动脉的受力分布情况;Nestola[10]等人研究主动脉瘤的生理和病理原因，仿真中心动脉和肺动脉分流的受力情况;Al-Rawi[11]等人评估了主动脉狭窄对血流和血压的影响;还有Caballero [12] 等人总结了过去10 年来腹腔动脉血流动力学研究的情况，发现相关的疾病与血管的病理性改变通常有一定的联系，但是人体腹动脉瘤等发病机制尚不明确。近年来，关于血流动力学变化在动脉瘤等心血管疾病形成机制中的作用日益受到国内外学者重视，并普遍认为动脉血管和血流动力学的参数与动脉疾病有着密切的关系。然而，在动脉血管和血液动力学研究中，大多采用简化的血管和血液模型，对真实接近人体复杂血管和血液的流体分析研究，在国内也尚不多见。本研究采用免费开源的SimVascular血管建模软件[13]和CFD方法，通过比较不同入口的血流速度初始条件，研究了复杂腹主动脉及其分支的血流速度流线、静态压力和壁面总剪切力的分布情况。

1    实验内容与方法

1.1  模型的建立

目前有较多的商业软件可以利用Computed tomography （CT）和Magnetic resource imaging（MRI）获取的医学血管数据，重建主要动脉血管的几何模型。然后导入到CFD软件包进行血流参数的仿真分析[14-15]。然而构建逼近人体动脉血管的3-D模型，需要经过复杂的操作过程才能完成[16，17]。为此，在2007年斯坦福大学的Charles Taylor[18]带领团队开发了SimVascular血流动力学仿真软件，经过多年的发展，目前已经成功开发出多种升级版本，适应于Windows、Linux和iOS三种主流的操作系统。该软件代码免费开源，方便自定义各种专业功能，操作简单易用。通过医疗图像数据SimVascular软件系统可以灵活高效地构建血管的3-D动脉模型，并且可以提供完整的网格划分和边界，定义一整套的血液动力学仿真计算。具体的模型构建过程如图1所示。

依据人体的双源CT血管数据，构建腹主动脉以及附近主要动脉的血管模型，模型包括57个面、56条边、20个顶点。具体包括主动脉干、腹腔动脉、腹腔动脉二分支、脾动脉及其一分支肝动脉、肠系膜上动脉及其二分支、肠系膜下动脉、左髂动脉及其三分支、右髂动脉及其三分支、左肾动脉，左肾上腺动脉，右肾动脉，右肾下动脉等主要腹腔内动脉。

根据以往学者的研究经验，血液定义为不可压缩的牛顿流体，血液的密度为1 060 kg/m3，黏度采用ANSYS  FLUET系统定义的卡罗流体模型参数，具体参数定义见参考文献[19]。入口条件：正常人体腹主动脉血流速度的最大值约为1.2 m/s。然而人类的心脏射血时间是周期性时变的，因此腹主动脉入口处的速度设定采用一种类抛物线定义的方案，未被設定为一个常数，而是采用带有时变周期性的函数[8]。在Fluent中定义UDF，收缩期的正弦波峰值速度为1.2 m/s，最小速度为为0.1 m/s;假设心率为75 次/min， 每个周期的持续时间是0.8 s。在上述入口条件下，又采用了另一种定值速度方案[20]，通过计算上述一个周期内的平均血流速度约为0.3 m/s，将其作为新的入口条件下再次进行计算。出口条件：设定所有出口初始条件的流动已经稳定，各个分支动脉输出压力设置为零，并且具有自然输出，本文没有使用解剖和生理学标准，通过合适的终端阻力双弹性腔模型来定义每个出口的条件[21，22]。壁面条件：管壁满足无滑移条件， 由于血管壁的径向速度非常小， 故将壁面的径向速度简化设定为零。

1.2  网格参数

显示血液几何的网格部分模型。将所建的几何模型导入到Workbench中，采用系统自带的ICEM进行网格划分。血液模型网格由四节点四面体单元构成，算法为自适应调整方法，内部节点全局调整规划。最后在标准单位下，得到网格的统计数据：模型中节点的数量是238341，元素是1188 703。所得到的网格最小尺寸是0.20，最大尺寸1.00，平均尺寸是0.83，标准偏差是0.098。可见划分的网格满足计算的最优标准。

1.3  仿真方法

使用商用的Fluent软件进行模拟计算，仿真基本理论是Navier-Stokes控制方程。在PISO方案中，采用Fluent中的瞬态模拟和压力速度耦合的双精度进行计算;残差检查收敛设置为0.000 1。 整个血流模型的计算从静态流体开始，采用定点模式计算，时间步长设置为0.1 s，时间步数为8，最大迭代次数为200 次，同时还设置每隔0.1 s保存一次计算的结果。 最后使用CFD-Post来处理整个范围从0 s到0.8 s的计算结果，提取每个时间段的计算结果，主要包括入口和出口的平均速度以及静态压力，壁面流体的剪切力等进行分析研究，分别给出了三个时间点T1（0.1 s），T2（0.2 s）和T8（0.8 s）的速度、静压力和壁面剪切力的图形结果。另外，还给出了两种方案仿真的对比结果。

2    仿真结果与分析

通过定义抛物线入口和平均值入口速度两种条件，得到腹主动脉以及髂动脉模型的流体仿真计算结果，总体情况如图4、5、6和7所示，观察对比模型仿真计算得到的血液速度流线图、静态压力图以及血管内壁面的剪切力图。主要进行腹主动脉及其分支的概念性结果仿真，没有做深入的血流粒子跟踪、具体位置血压的分析和双向的血管壁血压耦合效应等。

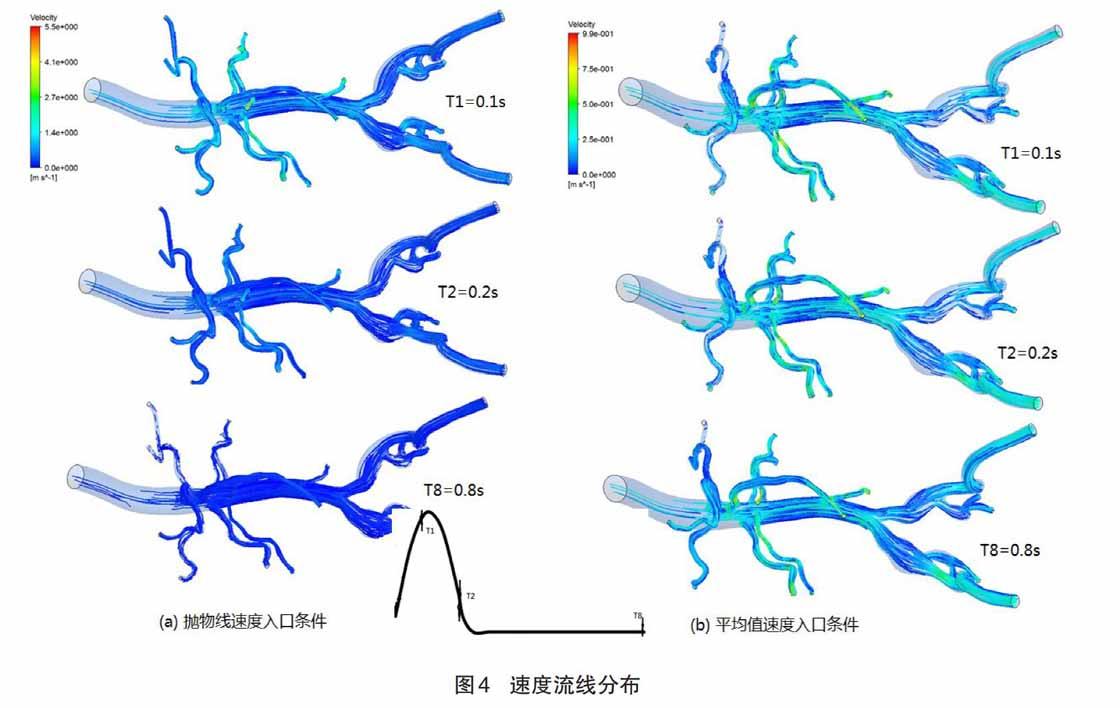
2.1  血流速度

给出两种不同入口速度条件下，采用不同标尺刻度，血管模型整体速度流线图变化的情況。图4（a）表示类抛物线速度入口条件下的计算结果，通过标尺的最大刻度值可以看出，血液在模型中的某处最大速度是5.5 m/s，是定义入口速度最大值1.2 m/s的4.58倍。在T1时刻，速度的最大值主要出现在模型血管的分叉处和血管直径较小处，具体分布在腹主动脉分叉处，左右肾动脉处，髂动脉分叉处。在T2时刻，因为入口速度的下降，可以看出腹主动脉腔的速度下降接近零值，只有小直径血管的远端血流速度大约是1.4 m/s。在T8时刻，因为入口速度一直是0.1 m/s，所以血管各处的速度流线图趋于稳定。图4（b）表示平均值速度入口条件下的计算结果，通过其刻度尺可以看出，血液在模型中的最大速度是0.99 m/s，是定义入口速度平均值0.3 m/s的3.3倍。在其T1、T2和T8时间点的速度流线图中，几乎观察不出区别，通过跟图4（a）结果进行对比，发现血管在分叉和小直径血管处，都出现较大速度。但是在肠系膜上动脉和左右髂动脉的远端出现明显的不同，在图4（b）中发现肠系膜上动脉远端有较大的速度。

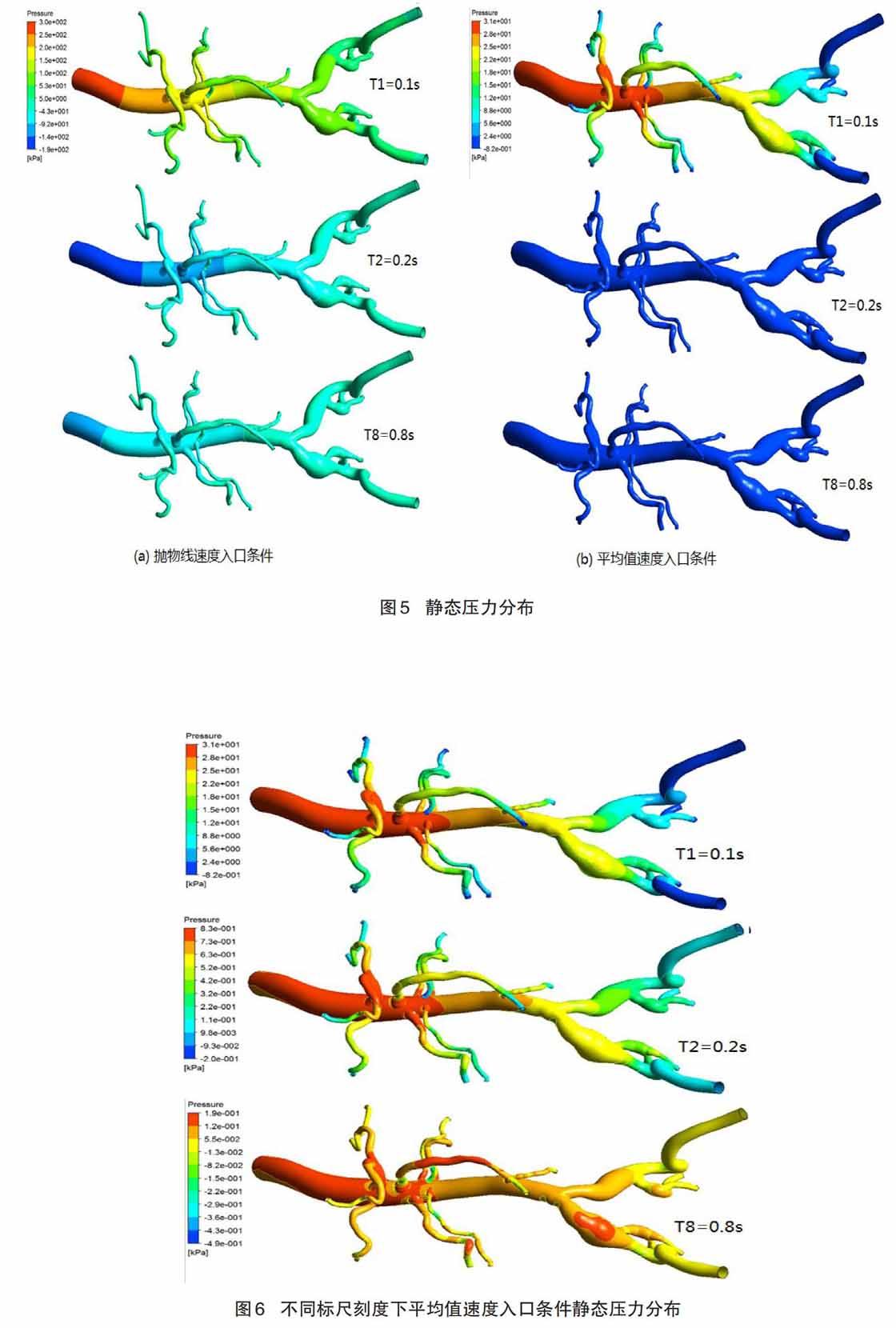
2.2  静态压力

表示两种不同入口速度条件，采用不同标尺刻度下，血管模型整体静态压力分布变化的情况。图5（a）表示类抛物线速度入口条件下的静态压力计算结果，通过标尺的最大刻度值可以看出，血液在模型中的入口处最大压力值是300 kPa，最小值是-190 kPa，据此看出血液存在着回流现象，跟实际临床观察到的现象一致。在T1时刻，压力的最大值主要出现在模型血管的入口处，同时发现从入口到远端被均匀的压力分段，每一段的压力值逐渐减小，最小值5 kPa出现在远端血管模型。在T2时刻，因为入口速度的下降，出现血液的回流，导致整个血管模型出现负压力值的分段，特别在入口处压力最小值是-190 kPa 。在T8时刻，由于入口速度一直稳定在0.1m/s，所以血管入口处压力逐渐增大，并且各处的压力值趋于稳定，但是压力分段出现明显。图5（b）表示平均值速度入口条件下的静态压力计算结果，通过其刻度尺可以看出，血液在模型中的入口处最大压力值是31 kPa，最小值是-0.82 kPa，据此可以看出在血流速度0.3 m/s的条件下，血液依然存在着回流现象。在其T1时刻，血管模型压力值分段较为明显， 腹主动脉入口处以及附近各分叉处都出现最大的压力值，且分布面积较大，分叉血管的远端出现较小面积的负压力值，但是在左右髂动脉的远端，出现大面积的回流现象，导致出现负压力值-0.82 kPa。在T2和T8时间点的静态压力图中，采用统一的标尺刻度值，几乎观察不出区别，血管模型整体压力值趋于负值。

为了能够清楚的观察到在平均值速度入口件下的静态压力计算结果，如图6所示，采用不同的刻度尺可以看出整个压力值随着时间变化的情况。在T1时刻，腹主动脉入口处出现最大压力值是31 kPa，在左右髂动脉的远端发现最小值-0.82 kPa。在T2时间点，入口处依然是压力的最大值0.83 kPa，跟T1时间点的最大值对比，下降了37.35倍。但是左右髂动脉以及小直径血管的远端没有出现负压力值，除了右肾下动脉分叉处。在T8时刻，腹主动脉入口处的压力最大值下降到0.19 kPa，观察发现整个血管模型是随着时间推移压力逐渐减小，主要是因为大量回流的影响。在腹主动脉腔分叉处、肠系膜上动脉中间段、右髂动脉血管模型直径变大处，出现较为明显的压力值。可见血管在流速较小的层流状态，可以发现不仅在小直径血管处会出现大压力，而且在大直径血管的分叉位置前，也会出现较大的静态压力。

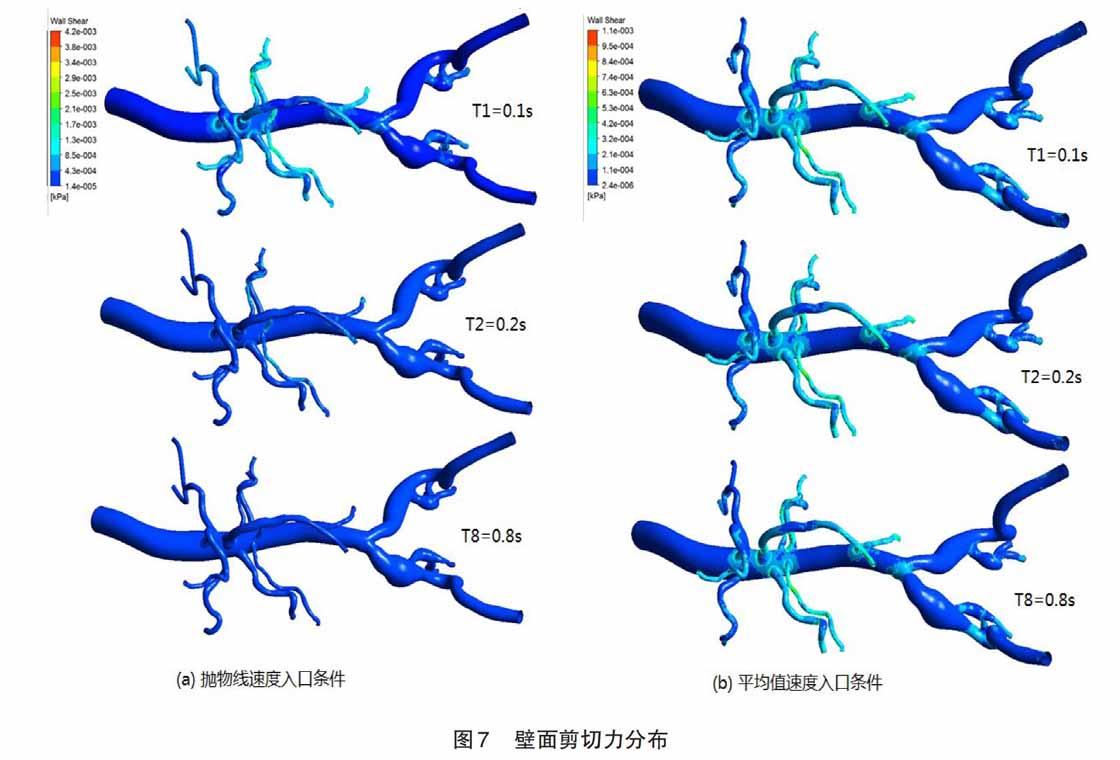
2.3  剪切力

给出两种不同入口速度条件，采用不同标尺刻度下，血管壁面整体剪切力分布变化的情况。图7（a）表示类抛物线速度入口条件下的壁面剪切力计算结果，通过标尺的最大刻度值可以看出，在模型血管壁面中出现的最大剪切力值是4.2 Pa，最小值是0.014 Pa。 在T1时刻，发现从腹主动脉入口处到远端没有均匀的剪切力分段出现，剪切力的最大值主要出现在模型血管的分叉处和血管直径较小处，具体分布在腹主动脉腔分叉处，肠系膜上动脉远端，左右肾动脉附近处，肠系膜下动脉，髂动脉分叉处。在T2时刻，壁面剪切力迅速下降到最小值， 除了左右肾上下动脉。在T8时刻，因为入口速度定义的是0.1 m/s，所以血管壁面各处的剪切力趋于稳定在最小值，其数值较小。图7（b）表示平均值速度入口条件下的剪切力计算结果，通过其刻度尺可以看出，在模型血管壁面中出现的最大剪切力值是1.1 Pa，最小值是0.002 4 Pa。通过跟图4（a）结果进行对比，发现血管模型的最大速度比在4倍的基础上，其出现最大剪切力的比值也接近4倍，证明其剪切力跟入口速度梯度之间的一定关系。在其T1、T2和T8时间点的壁面剪切力图中，几乎观察不出区别，通过跟图4（a）结果进行对比，发现血管在分叉和小直径血管处，都出现一致的剪切力分布结果。

3    讨论

动脉血管是分布于人体内部大小不一的管腔状结构，是人体器官系统执行其生理功能的重要基础。各类心脑血管疾病是由于不同的血液动力学参数因素引起，这些因素不仅取决于血管的复杂程度和几何形状，而且还受到血液的流变特性影响[23]。目前临床医学的解决方案仅限于简单症状，花费高昂的测试费用，浪费大量的时间精力。为此，随着计算机建模技术的发展，采用CFD仿真计算已被认可和有效地用于解决这些问题。通过开源的SimVascular软件，依据双源CT血管数据，成功构建复杂的腹主动脉及其分支的血管模型，如图2所示，基本满足三维血管节段、迂曲度、长度、截面积、血管分支与血管网络三个层次的定量特征指标[24]，特别在分支的指标上，具体体现在主要分支数、终端分叉数、各类节点数、分叉角度和内分叉距离等参数。能够起到抛砖引玉的作用，使得构建大型复杂人体血管网络模型成为可能，同时促进复杂血管模型双向流固耦合的进程。

根据图4的血流速度流线分布图，可以看出在不同速度条件下，血管各位置点血流速度随着时间的变化趋势。在类抛物线入口条件下，当入口速度达到最大时，血管的局部位置要承受其近5倍速度的冲击。同理在定值低速入口条件下，血管局部位置要承受其入口速度3倍多的血流冲击，这些位置主要分布在血管的分叉处和小血管处。依据这两种条件的计算结果，发现入口速度的逐渐增加，会加倍血管各分叉处的速度，可见随着年龄的增长，心脏射血的速度逐渐增大，同样就会增加血管某处的超倍速度，影响血流和血管的各类性能参数。另外，发现血流是定值时，对血管的影响将会更大，持续时间更长。当然正常人体心脏的供血是瞬态的，但是随着年龄的增长和某疾病的影响，会导致血流速度出现短暂的定值或者接近定值，对人体的心脑血管系统将会增加一定的影响。

通过对图5静态压力的仿真结果分析，发现在最大入口速度值1.2 m/s是定值0.3 m/s速度4倍的情况下，在入口处计算出的最大静压力值300 kPa是定值速度入口条件下静态压力值31 kPa的大约10倍。然而最小值之间的差别更加明显，通过比较最小值发现，随着入口速度的增大，血流的回流现象较明显。按照正常的流体力学理论，在定值速度入口条件下，流体不应该出现回流的现象。而仿真结果如图6所示不同标尺刻度下平均值速度入口条件静态压力分布，发现静态压力在随着时间周期的增大，整体压力段在逐渐减小，入口处静压力从31 kPa逐渐减少到0.19 kPa。分析其中原因，定义的流体是血液的密度特征，黏度采用的卡罗流体模型参数。当然本研究结果也许存在着一定的局限性，使得血液流体的计算结果和真实流体情况有所差别，留在今后的研究工作中做进一步研究。

较多的学者研究证实，壁面剪切力以及其梯度被认为在血管再狭窄的过程中扮演着重要的角色，非生理性剪切力会触发内膜增生和动脉粥样硬化板块形成，为血管再狹窄的出现提供病理基础[25]。发现在血管和支架段内出现壁面剪应力低于0.5 Pa 的区域为内膜增生易发区，应尽量减少这种低壁面剪应力的区域[26]。依据图7的计算结果，证实剪切力跟速度之间的正比关系，同时发现在血管分叉处和小血管处出现较大的剪切力，在不同速度入口条件下，剪切力的分布位置基本一致。如果依据血管壁面剪切力出现小于0.5 Pa的区域是内膜增生易发区，可以看出入口速度在0.3 m/s的条件，计算出血管模型大面积出现剪切力低于0.5 Pa，引起血管内膜增生可能性较大。

4    结论

本文基于开源SimVascular血管建模软件和商用ANSYS软件，对腹主动脉血流动力学进行了仿真研究。采用双源CT血管造影医学数字图像数据，成功构建了复杂人体的多分支腹主动脉以及髂动脉血管模型。假设血管模型血流为层流、不可压缩牛顿流体，卡罗流体模型参数、入口血液流速随时间类抛物线变化和平均定值两种初始条件，应用ANSYS FLUENT软件进行血流仿真计算和分析，获取复杂腹主动脉及其分支的血流速度流线、静态压力和壁面总剪切力的分布情况。仿真结果发现：血管在分叉和小直径血管处，都出现较大速度和剪切力，但是在肠系膜上动脉和左右髂动脉的远端出现明显的不同;入口速度的逐渐增加，会加倍血管各分叉处的速度;在平均值速度入口条件下，静态压力在随着时间周期增大，整体压力段在逐渐减小。 当然本研究结果也许存在着一定的局限性，如简化血管的长度、忽略重力和仅采用层流一种模式，使得血液流体的计算结果和真实流体情况有所差别，留在今后的研究工作中做进一步研究。综合上述研究成果，成功构建复杂腹主动脉血管网络拓扑结构并进行仿真计算，将有助于临床医生更深入理解各个位置处动脉血流力学特征，并为临床诊疗腹主动脉血管疾病提供一定的参考价值。

致   谢

仿真实验在构建模型过程中得到常州市第二人民医院曹海涛和刘炜医生的大力支持及多方面的帮助，在此致以诚挚的感谢！

参考文献：

[1] 张丹，李彩英，高不郎，等.颅内动脉瘤血流动力学发病机制研究进展[J].介入放射学杂志， 2017，26（4）：378-382.

[2] ASSEMAT P，ARMITAGE J A，SIU K，et al.Three-dimensional numerical simulation of blood flow in mouse aortic arch around atherosclerotic plaques[J].Science Direct，2014，38：4175-4185.

[3] 陈宇，李睿，赵雪梅，等.基于医学影像的血流动力学分析[J].力学发展，2016，46：323-342.

[4] 郑河荣，刘家好，何玲娜.脑血管计算机模型的建立与有限元分析[J].浙江工业大学学报，2014，42（3）：253-256.

[5] SAHO T，ONISHI H.Quantitative comparison of hemodynamics in simulated and 3D angiography models of cerebral aneurysms by use of computational fluid dynamics[J].Radiological physics and technology，2015，8（2）：258-265.

[6] 陈珍，袁奇，朱光宇，等.颈内动脉狭窄时Willis环的血液动力学数值模拟[J].西安交通大学学报，2009，43（10）：119-123.

[7] POTTERS W V，CIBIS M，MARQUERING H A，et al.4D MRI-based wall shear stress quantification in the carotid bifurcation： a validation study in volunteers using computational fluid dynamics[J].Journal of Cardiovascular Magnetic Resonance，2014，16（S1）：162-163.

[8] 劉莹，罗院明，殷艳飞，等.动脉内流-固耦合作用下两相血流动力学数值模拟[J].介入放射学杂志， 2017，26（3）：253-257.

[9] 孙正，刘存.基于血管内超声的动脉血管壁应变分布的计算流体力学仿真[J].生物医学工程学杂志，2015，32（6）：1244-1248.

[10] NESTOLA M G C，GIZZI A，CHERUBINI C，et al.Three-band decomposition analysis in multiscale FSI models of abdominal aortic aneurysms[J].International Journal of Modern Physics C.2016，27（2）：1650017.

[11] AL-RAWI M，AL-JUMAILY A M.Assessing abdominal aorta narrowing using computational fluid dynamics[J]..Medical & biological engineering & computing，2016，54（5）：843-853.

[12] CABALLERO A D，LAIN  S. A. Review on Computational Fluid Dynamics Modelling in Human Thoracic Aorta[J].Cardiovascular Engineering and Technology，2013，4（2）：103-130.

[13] UPDEGROVE A，WILSON N M，MERKOW J，et al.SimVascular： An Open Source Pipeline for Cardiovascular Simulation[J]. Annals of biomedical engineering，2017，45（3）：525-541.

[14] SOUDAH E，ROSSI R，IDELSOHN S，et al. A reduced-order model based on the coupled 1D-3D finite element simulations for an efficient analysis of hemodynamics problems[J].Computational Mechanics，2014，54（4）：1013-1022.

[15] SOUSA L C，CASTRO C F，ANTONIO C C，et al. Toward hemodynamic diagnosis of carotid artery stenosis based on ultrasound image data and computational modeling[J]..Medical & biological engineering & computing，2014，52（11）：971-983.

[16] 刘波，李志伟.数值模拟描述血管壁厚度对复杂颅内动脉瘤流固耦合分析结果的影响[J].中国组织工程研究，2014，18（11）：1765-1773.

[17] 乔爱科，侯映映，阳侯.冠状动脉狭窄几何构型对血流储备分数影响的有限元分析[J].中 国 生物 医 学工程学报，2015，34（2）：199-204.

[18] TAYLOR C A，HUGHES T J R，ZARINS C K.Finite Element Modeling of Three-Dimensional Pulsatile Flow in the Abdominal Aorta： Relevance to Atherosclerosis[J].Annals of biomedical engineering，1998，26：975-987.

[19] WU Q Y，LIU X J，PAN L J，et al.Simulation Analysis of Blood Flow in Arteries of the Human Arm[J]. Biomedical engineering ： applications， basis， and communications，2017，29（4）： 1750031-1750038.

[20] 吕绍茂，钟华，陈丽君，等.构建颈内动脉瘤双向流固耦合模型的血流模拟[J].中国组织工程研究，2014，18（2）：218-225.

[21] OLUFSEN M S，NADIM A，SELGRADE J F.On Dedriving Lumped Models For Blood Flow And Pressure In The  Systemic Arteries[J].Mathematical Biosciences  And Engineering，2004，1（1）：61-80.

[22] GHARAHI H，ZAMBRANO B A，ZHU D C， et al.Computational fluid dynamic simulation of human carotid artery bifurcation based on anatomy and volumetric blood flow rate measured with magnetic resonance imaging[J].International journal of advances in engineering sciences and applied mathematics，2016，8（1）：40-60.

[23] JAHANGIRI M，SAGHAFIAN M，SADEGHI M R.Numerical simulation of non-Newtonian models effect on hemodynamic factors of pulsatile blood flow in elastic stenosed artery[J].Journal of Mechanical Science and Technology，2017，31（2）：1003-1013.

[24] 郏科人，吴英成，裘茗烟，等.血管三维结构定量特征指标研究进展[J].中国数字医学，2017，12（7）：1-20.

[25] 魏延宾，程洁.脉动流下血管支架耦合系统血流动力学实验研究 [J].生命科学仪器，2017，15（4）：28-32.

[26] 张业鹏，周敏，汤文浩.生物可降解血管支架的血流动力学数值模拟[J].中国组织工研究，2017，21（34）：5532-5537.

Abstract： This paper studies the simulation calculation for the variation of hemodynamics parameters in human abdominal aorta and iliac artery under different blood flow velocities at the entries. And it adopts open source software SimVascular to construct the vessel models of abdominal aorta and some major arteries nearby including celiac axis， celiac artery， splenic artery and its hepatic artery branches， superior and inferior mesenteric arteries， left and right renal arteries and iliac arteries according to the CT vessel data. Besides， this paper mainly analyzes the blood velocity vector， static pressure， and wall shear stress by using the Fluent simulation calculation. Finally， the quasi-parabolic-like function velocity and the average constant velocity were assigned at the entry respectively， and it was found that in both conditions， the arterial models appeared larger velocities and wall shear stresses at the bifurcation and small-diameter vessels. However， there were significant differences between the superior mesenteric artery and the distal end of the left and right iliac arteries. At the same time， it was also found that the gradual increase in the entry speed would double the speed of the bifurcation artery. In conclusion， the successful construction of complex arterial networks and the results of simulation will help doctors better understand the characteristics of arterial blood flow.

Key  words： major celiac arteries; velocity vector; static pressure; wall shear stress; hemodynamics

責任编辑    张志钊