利用多元统计分析三明市工业污染治理的综合评价
2019-09-24张启贤
张启贤,赵 华
(1.三明学院 信息工程学院,福建 三明 365004;2.工业大数据分析及应用福建省高校重点实验室,福建 三明 365004)
随着全球工业化进程的加快, 工业所带来的环境污染和生态破坏已经威胁到人类的生存和发展,而且还直接制约着经济增长。 当今工业的迅猛发展造成了自然资源和能源的过度开采与大量消耗,产生了大量有毒有害的废弃物,对人类生存环境造成了严重污染[1]。 “十三五”规划时期,生态文明建设已上升为国家战略,保护环境成为了全民关注的焦点。 因此,有效控制工业污染排放量,分析研究工业污染治理,提高工业污染治理效率,对国民经济可持续发展起着重要作用。 现有文献对工业污染治理做了大量的研究,例如文献[2]分析了地方政府工业污染治理的现状及对策;文献[3]针对工业区地下水的规划治理,根据地下水的特性分析了工业区地下水污染源及分布状况,并提出了地下水规划治理的具体措施;陶瓷行业作为工业污染防治重点行业之一,文献[4]对建筑陶瓷企业的废气现状进行了分析且给出了优化改进建议。 特别地,文献[5]对京津冀工业污染治理现状进行了比较并研究了其相应对策研,文献[6]结合京津冀钢铁行业废气排放现状对国内外相关地区进行比较并给出了相应的对策研究,文献[7]结合国家环境保护标准《制浆造纸工业污染防治可行技术指南》对我国制浆造纸工业污染现状和防治对策进行了研究。 在定量研究方法上主要是:DEA 模型法[8-11]、Malmquist 指数法[12-13]以及两者相结合的DEA-Malmquist 模型[14]。工业污染已经威胁到人类的生存和发展,直接制约着经济增长。 研究工业污染治理,提高工业污染治理效率,有利于国民经济可持续发展[15-16]。 目前针对三明市工业污染治理综合评价的定量研究较少,本文先应用主成分分析方法得出三明市12 个县(市、区)工业污染治理的综合得分和排名,然后再利用聚类分析方法,对三明市各县(市、区)工业污染治理进行分类,并做出综合评价。
1 数据的来源
工业污染是指工业企业在生产过程中所形成的废气、废水和固体排放物对环境的污染。 污染主要是由生产中的“三废”(废水、废气、废渣)及各种噪音造成的。 鉴于三明市噪声的等效声级“较好”,本文在工业污染治理分析中,没有考虑噪音污染的治理。
数据来源于三明市统计年鉴(2017),选取了工业污染治理的5 个指标数据,来评价三明市工业污染治理情况:工业固体废物利用率(X1)、废水治理设施运行费用(X2,单位:万元)、废气治理设施运行费用(X3,单位:万元)、废水治理设施处理能力(X4,单位:万 t/d)、废气治理设施处理能力(X5,单位:万 m3/h)。 经整理见表 1。
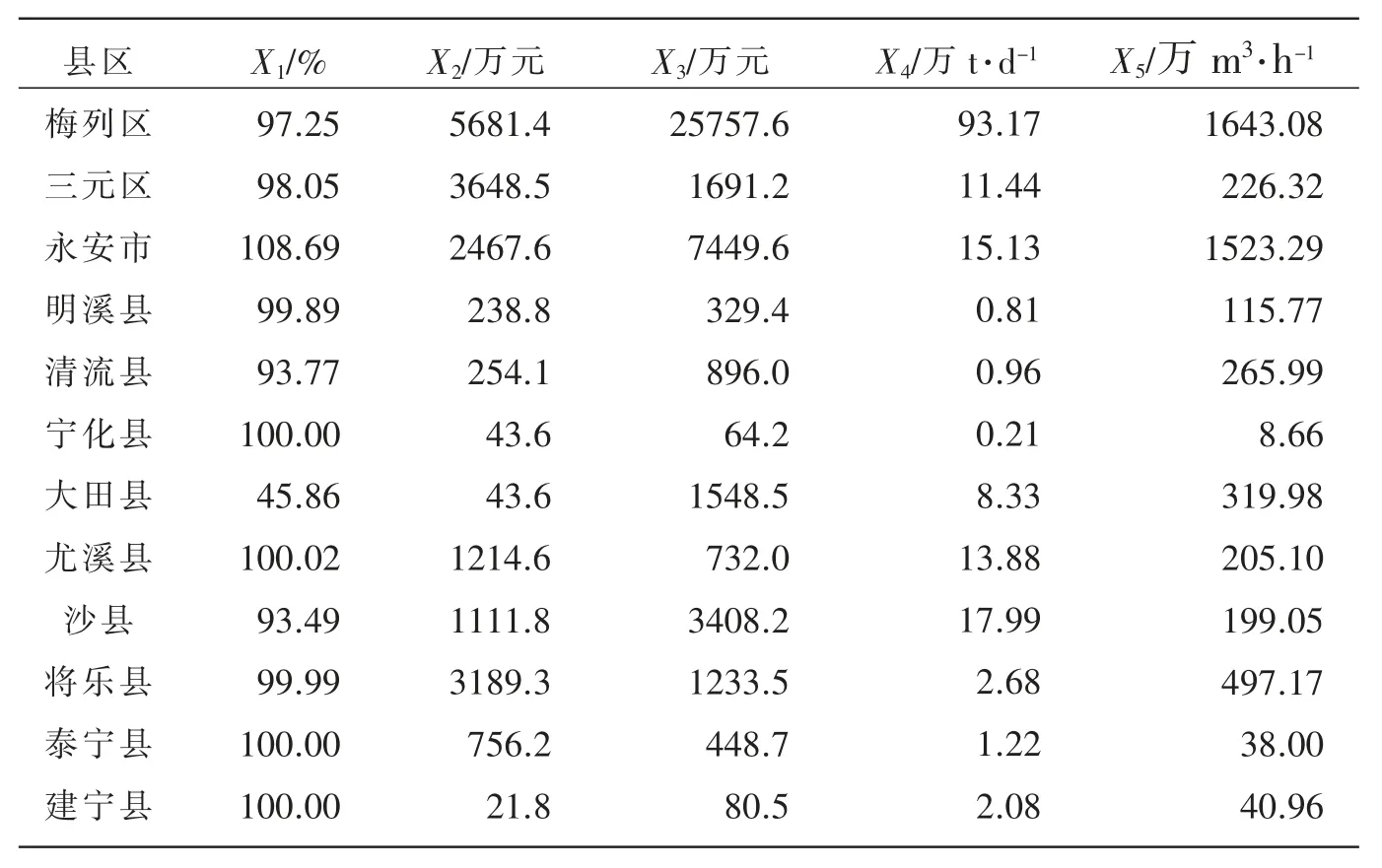
表1 三明市工业污染治理指标数据
由于选取的指标具有不同的量纲,为了消除其对数据计算带来的影响,进行主成分分析之前,先把数据标准化这里分别为 Xj的样本均值和样本标准差,记三明市工业污染治理指标标准化数据见表2。
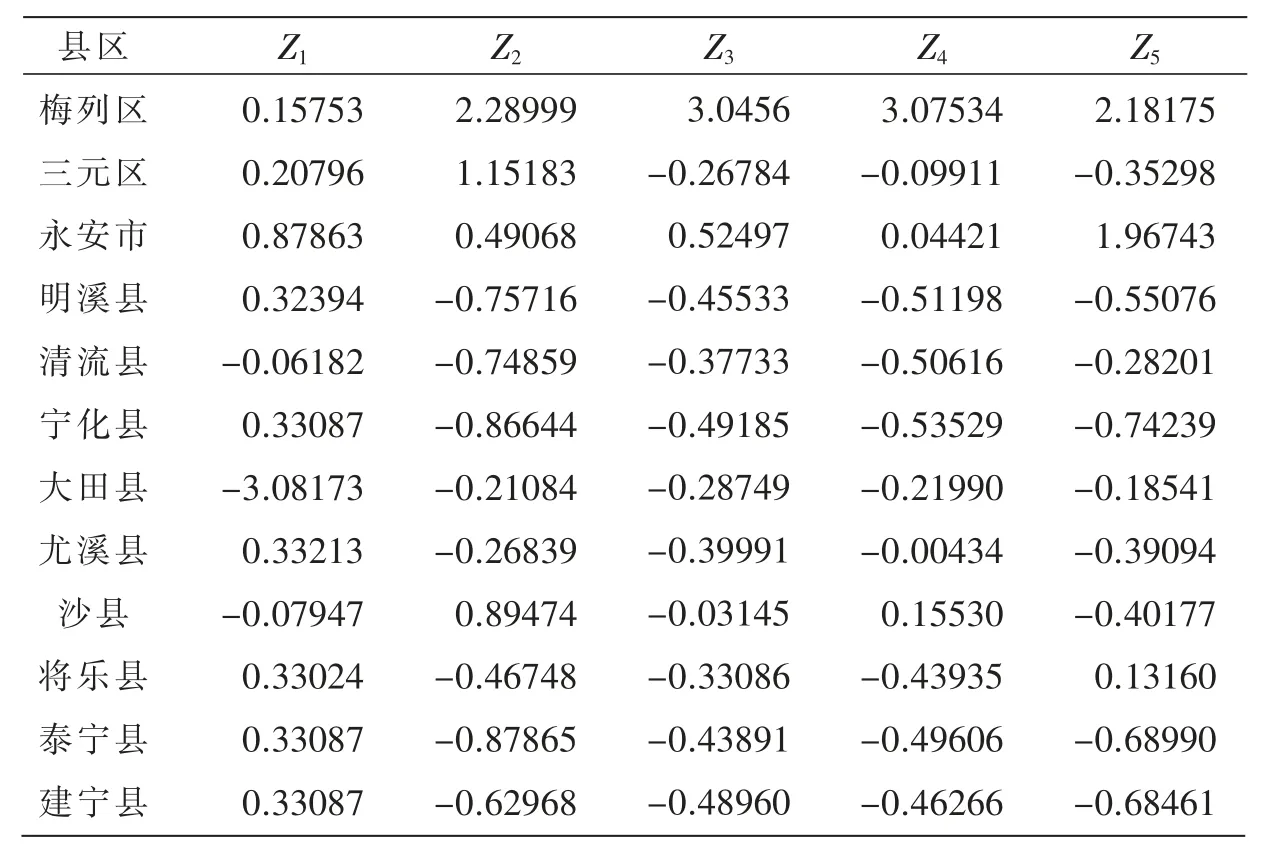
表2 三明市工业污染治理指标标准化数据
2 三明市工业污染治理主成分分析
主成分分析是将多个指标转化成少数几个互不相关的综合指标, 使这些综合指标尽可能多的代表原来指标信息量的一种多元统计方法。 通常用一个或几个新的指标把原始数据中的多个指标线性表示出来,用新的指标来提取出原始数据中的信息。 所以,通过主成分方法处理后的数据既降低了原数据的复杂程度,又最大限度的保留了原始信息[17]。
主成分分析综合评价步骤如下。
(1)将原始数据标准化;
(2)建立标准化后的P 个指标相关系数矩阵R;
(3)求 R 的特征根 λi(λ1≥λ2≥…≥λp)>0 和对应的单位正交特征向量 μi=(μ1i,μ2i,…,μpi)T,i=1,2,…,p;
(4)计算各主成分的方差贡献率αk及累积方差贡献率α(k);第k 个主成分Yk的方差贡献率前k 个主成分的累计贡献率
(5)确定主成分个数,并写出主成分表达式;主成分个数k 的确定:满足前k 个主成分的累计贡献率主成分表达式是标准化数据。
(6)计算综合得分
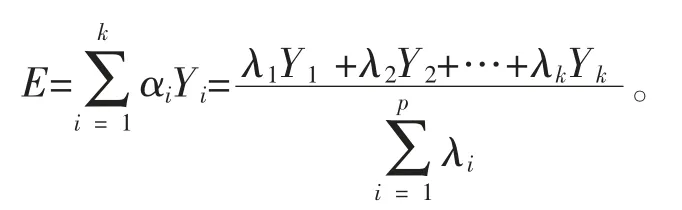
先对数据进行适宜性检验, 以确保样本是否适合做主成分分析。 利用SPSS 软件中的KMO 与Bartlett’s 球形度检验来测定,如果KMO 统计量接近1,做主成分分析的效果越好,低于0.5 不适宜做主成分分析。 对表 2 中的数据进行测定,结果如下表 3 所示。 由于 KMO 值为 0.759>0.500,Bartlett’s球形度检验卡方值为0.000,适合做主成分分析。
利用主成分分析得到起始因子的同时采用方差极大法进行因子旋转,通过SPSS 统计软件的计算,得到特征值、方差贡献率及累计方差贡献率,见表4。 由于前两个主成分的累计方差贡献率为89.639%,因此选用前两个主成分作为三明市工业污染治理评价指标。

表3 KMO 与 Bartlett’s 球形度检验
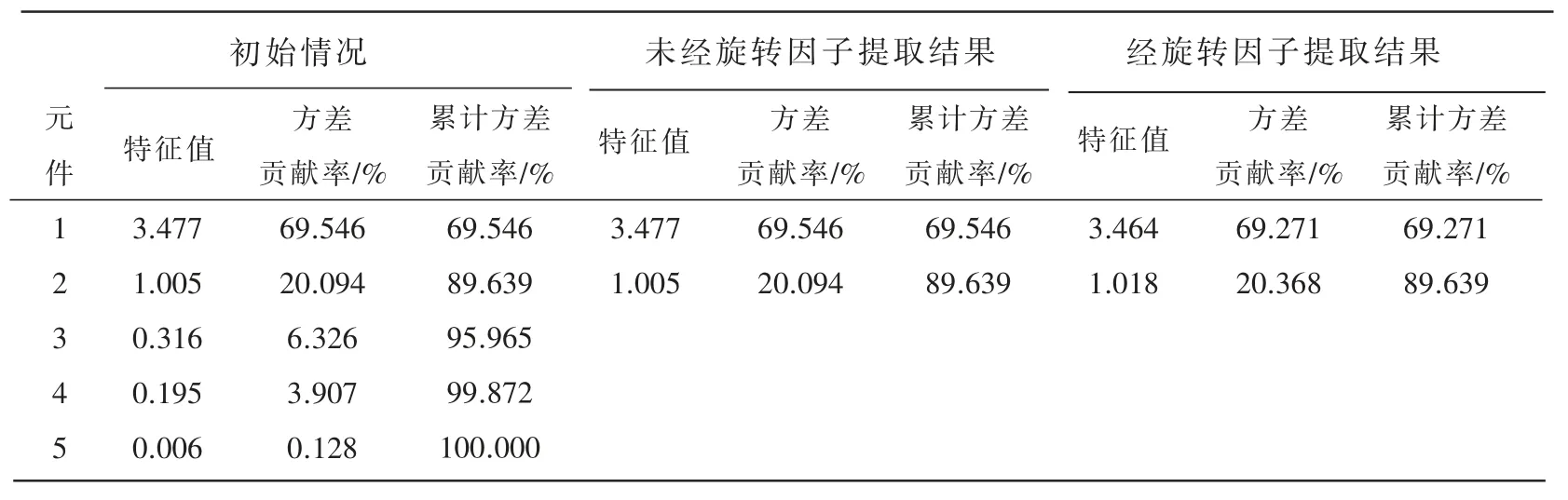
表4 特征值与方差贡献率
因子载荷矩阵显示出原变量与主成分之间的关联度, 因子载荷越高, 其包含的变量信息就越多。 表 5 为经过旋转后的因子载荷矩阵。 从中可以看出:主成分 1 对指标 X2、X3、X4、X5有较大载荷,表明这4 个指标之间相关性较强,命名为废水废气污染治理因子;主成分2 对指标对指标X1有较大负荷,命名为固体废物污染治理因子。
表6 为因子得分系数矩阵,由此可得两个主成分。
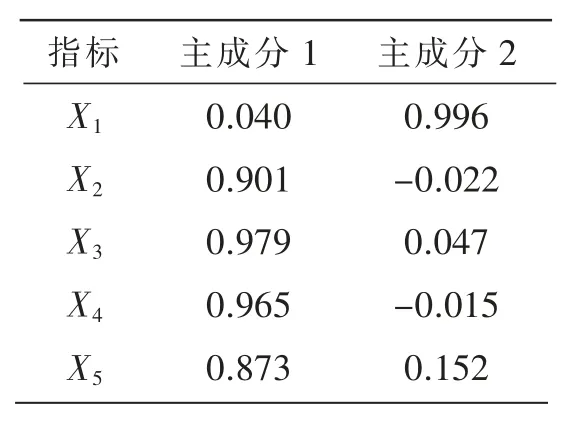
表5 旋转后因子载荷矩阵
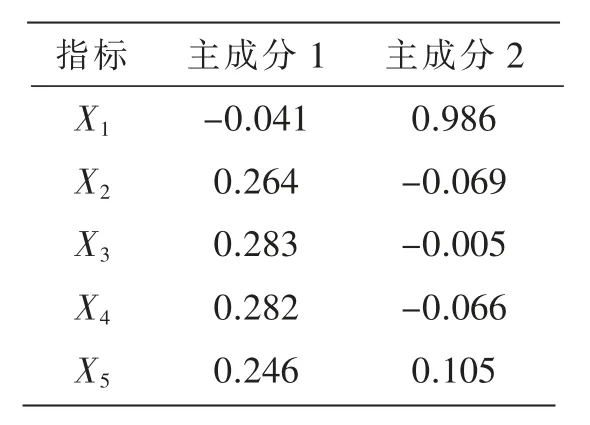
表6 因子得分系数矩阵
第一主成分:Y1=-0.041Z1+0.264Z2+0.283Z3+0.282Z4+0.246Z5, 第二主成分:Y2=0.986Z1-0.069Z2-0.005Z3-0.066Z4+0.105Z5,其中 Z1~Z5是标准化数据。
记v1为主成分1 的方差贡献率,v2为主成分2 的方差贡献率,则 v1=69.271%,v2=20.368%。 综合得分为
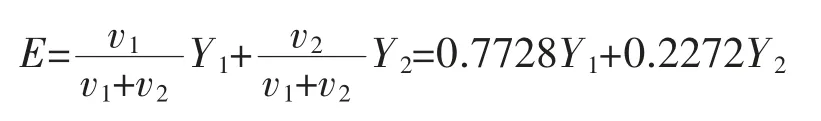
由SPSS 软件计算得到三明市12 个县(市、区)工业污染治理的主成分得分、综合得分及排名,见表7。
表7 中,可以看出三明市12 个县(市、区)的工业污染治理按综合得分E 从高到低的排名是梅列区、永安市、三元区、沙县、将乐县、尤溪县、清流县、明溪县、建宁县、泰宁县、宁化县、大田县。 其中废水废气污染治理因子Y1得分排名前三位是梅列区、永安市、沙县,后三位是明溪县、泰宁县、宁化县;固体废物污染治理因子Y2得分排名前三位是永安市、将乐县、明溪县,后三位是清流县、沙县、大田县。
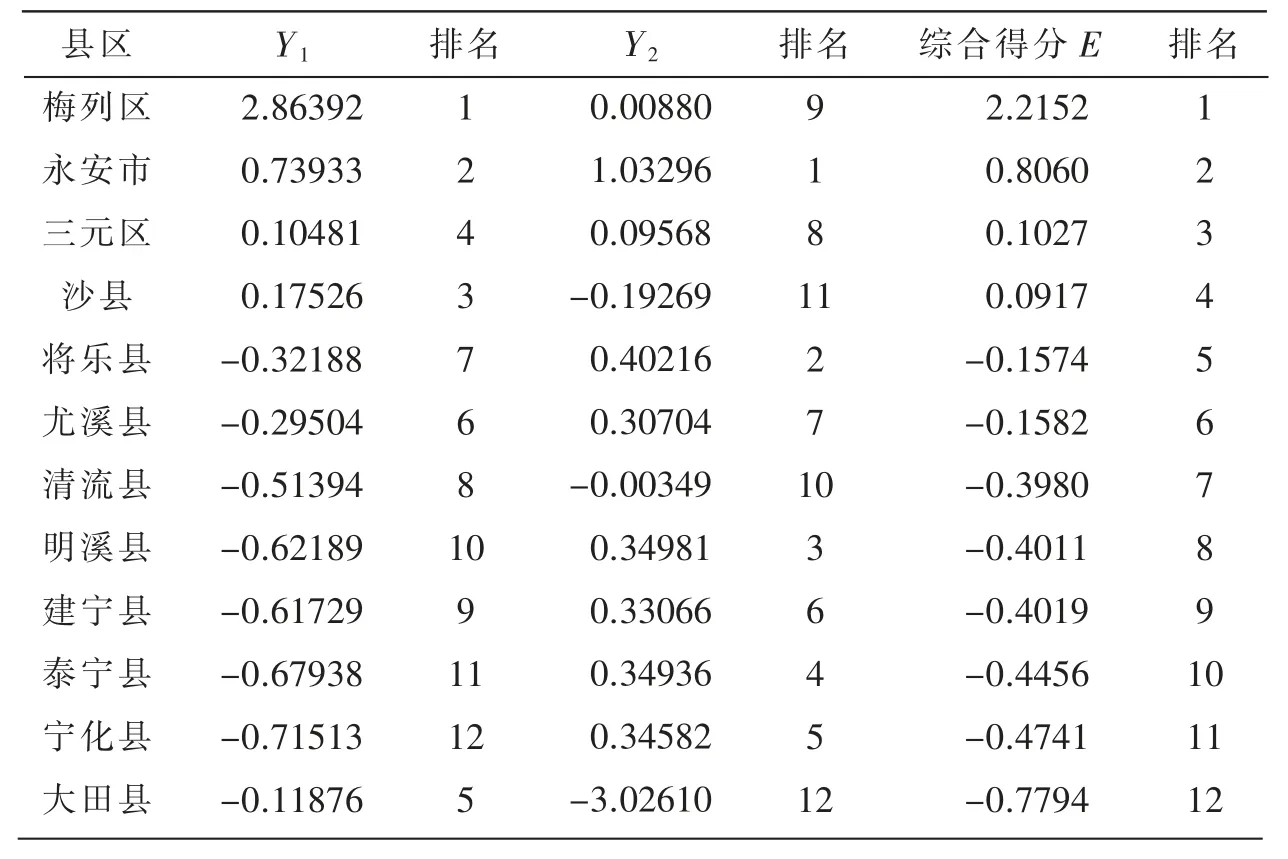
表7 三明市12 个县(市、区)工业污染治理得分及排名
3 三明市工业污染治理聚类分析
聚类分析是对样本(或指标)进行分类的一种多元统计分析方法。 这里采用有序样品聚类分析法,要求样品按一定的顺序排列,分类时不能打乱次序,即同一类样品必须是次序相邻的。
有序样品聚类法步骤[18]如下。
(1)定义类的直径
设 X(i),X(i+1),…,X(j)为某一类 G 中的样品,则该类的均值向量为
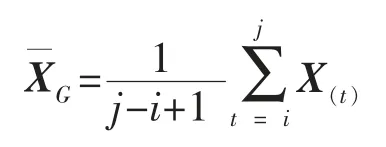
这一类的直径为
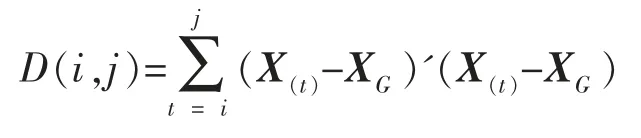
(2)定义分类的损失函数
若有 n 个有序样品,将其分为 k 类,记分法 b(n,k)为
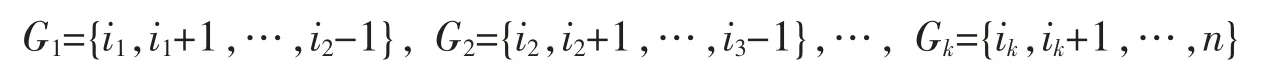
其中 1=i1<i2<…<ik<n=ik+1-1 分点为。 分类方法的损失函数为
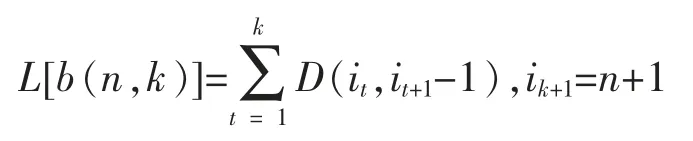
(3)导出 L[b(n,k)]的递推公式
当 n 和 k 为固定值时,L[b(n,k)]越小,分类方法的损失函数的效果越好,分类越有效。 当某种分法 b(n,k)的损失函数 L[b(n,k)]最小时,这种分法称为最优分类方法,记为 p(n,k)。
当 k=2 时,取 j*使得 L[b(n,2)]=D(1,j)+D(j,n)最小,那么可得最优解为
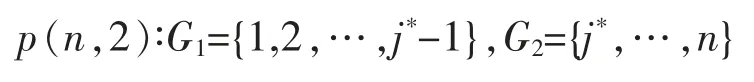
若要将n 个样品最优分割为k 类,则要对任意的j(k≤j≤n),先把前面j-1 个样品最优分割成k-1 类,得到 p(j-1,k-1),否则从 j 到 n 最后一类就不能构成 k 类的最优分割。 再考虑使 L[b(n,k)]最小的 j*,得到 p(n,k)。 那么 L[b(n,k)]的递推公式为
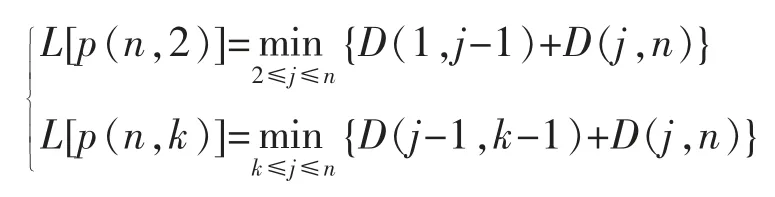
(4)求解最优分割
从 L[b(n,k)]的递推公式中可知,要得到分点 jk,使
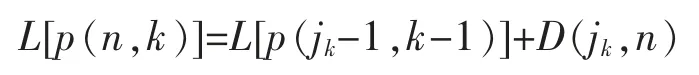
从而获得第 k 类:Gk={jk,…,n},必须先计算 jk-1使
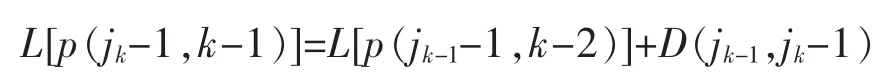
获得第 k-1 类:Gk-1={jk-1,…,jk-1}。
类似的方法依次可得最优分割 G1,G2,…,Gk。
以下使用R 语言进行聚类分析。 根据表7 中三明市12 个县(市、区)的工业污染治理综合得分,通过 R 语言的计算,求得类直径(见表8)和最小损失函数{L[p(l,k)]}(见表9)。

表8 直径 D(i,j)
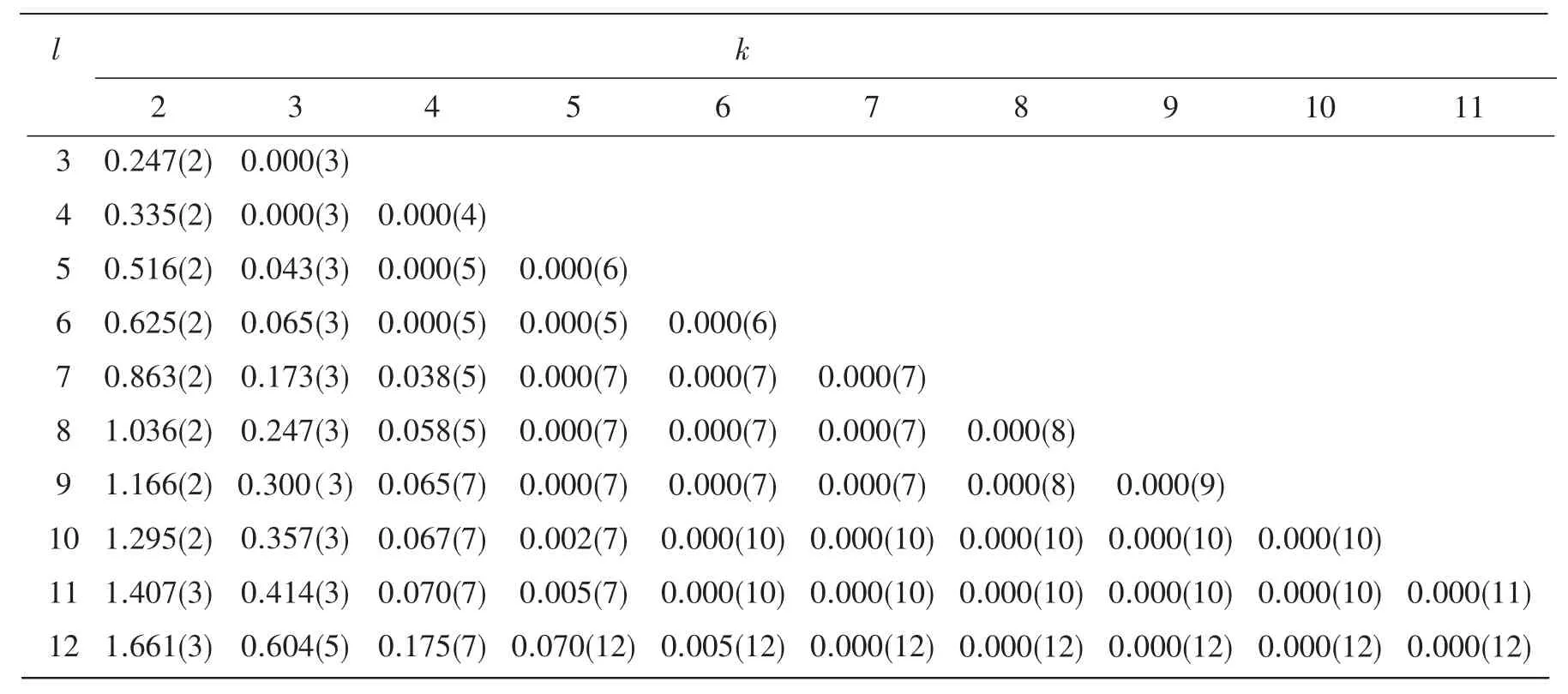
表9 最小分类损失函数 L[p(l,k)]
从表9 可知,k=3 时有明显拐点,因此,将其分为3 类。 运行R 软件可得三明市12 个县(市、区)工业污染治理聚类分析结果是:第1 类为梅列区;第2 类为永安市、三元区、沙县;第3 类为将乐县、尤溪县、清流县、明溪县、建宁县、泰宁县、宁化县、大田县。
聚类分析的分类结果与主成分分析的各县(市、区)工业污染治理综合得分排名基本一致。 第1类梅列区,工业污染治理综合得分排名第一,该类工业污染治理程度好;第2 类永安市、三元区和沙县,工业污染治理综合得分排名分别为第2、第3 和第4,该类工业污染治理程度一般;第三类的工业污染治理综合得分排名都靠后,该类工业污染治理程度较差。
4 结论
本文从三明市统计年鉴(2017)中,选取了工业污染治理的5 个指标数据(工业固体废物利用率、废水治理设施运行费用、废气治理设施运行费用、废水治理设施处理能力和废气治理设施处理能力),应用多元分析对三明市12 个县(市、区)的工业污染治理进行综合评价。
通过主成分分析,得出三明市12 个县(市、区)工业污染治理的排名,按综合得分从高到低依次为:梅列区、永安市、三元区、沙县、将乐县、尤溪县、清流县、明溪县、建宁县、泰宁县、宁化县、大田县。在废水废气污染治理中,排名前5 的是:梅列区、永安市、沙县、三元区、大田县。在固体废物治理中,排名前5 的是:永安市、将乐县、明溪县、泰宁县、宁化县。 通过聚类分析,将三明市12 个县(市、区)工业污染治理分为3 类,第1 类:梅列区;第2 类:永安市、三元区、沙县;第 3 类:将乐县、尤溪县、清流县、明溪县、建宁县、泰宁县、宁化县、大田县。 综合主成分分析和聚类分析的结果,可以得出三明市12 个县(市、区)工业污染治理程度:梅列区较好;永安市、三元区、沙县中等;将乐县、尤溪县、清流县、明溪县、建宁县、泰宁县、宁化县、大田县相对较差。 由上述分析并结合现实情况做出如下论述。
(1)梅列区的工业污染程度相对较重,工业污染治理程度好。 主要污染为废气污染和固体废物污染,工业污染治理中,梅列区注重水体污染的治理,比较轻视固体废物的治理,因此,在以后的治理中首要解决固态废物的污染和废气污染。
(2)永安市、沙县的工业污染程度较大,工业污染治理程度较好。 永安市的主要污染为废气污染、固体废物污染和水体污染,对其治理情况也较好。 沙县水体污染较为严重,废气污染和固体废物污染较轻,在工业污染治理中,水体污染和废气污染治理中等。
(3)三元区、尤溪县、大田县、将乐县、建宁县的工业污染程度中等,工业污染治理中,三元区治理程度中等,尤溪县、大田县、将乐县、建宁县治理程度较差。
(4)清流县、宁化县、明溪县、泰宁县工业污染程度较轻,工业污染治理程度相对较差。 但在固体废物污染治理中,明溪县、泰宁县、宁化县较好。
为改善三明市工业污染情况及治理投资投入不合理的现状,政府应加强广大市民的环保意识,完善公众参与机制。 积极调动和发挥媒体的力量,形成良好的宣传效果。 并且加大环境保护信息公开力度,全方位公开环境评估、审批信息、环境执法信息和重点企业环境自行监测信息,保障公众的知情权。 同时还应加大对科技创新与人才培养的支持力度。 政府部门要加大投入科技研发的经费,支持研发部门的环境保护项目,加大对技术人才的培养,定期对人才进行外出深造,深入学习好的技术知识,增加技术人员的福利待遇,以防人才流失。
以上分析可看出三明各县(市、区)的工业污染治理存在着显著差异。 因此,还需进一步加大对三明市工业污染的治理力度,重点区域重点防护重点治理。 有效的控制工业污染排放量,不断优化河道上下游的工厂企业布局,增大企业自身的环保意识与污水处理能力。 提高工业污染治理效益,加大各级部门的监管、监控、监察力度,大力发展低碳经济,保障国民经济可持续发展,加快实现“河畅、水清、岸绿、景美”的三明市。
