浅谈如何在小学数学课堂教学中有效渗透数学思想方法

张长山

(安徽省滁州市南谯区腰铺中心小学 安徽 滁州 239057)

数学新课程标准总体目标明确指出“通过义务教育阶段的数学学习,学生能够获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”。由此可见,数学的思想方法是数学的灵魂和精髓。众所周知,课堂教学是教育教学的主阵地,而在课堂教学中有效地渗透数学思想方法,既是提高数学教学质量的关键,也是培养学生发现问题、分析问题和解决问题的关键。那么究竟该如何在课堂教学中有效渗透数学思想方法呢？下面我想联系自己的教学实践,从两个方面来谈谈对这个问题的一些浅显认识。

1.抓住课堂教学的三个关键环节,有效地渗透数学思想方法

十多年的数学教学实践告诉我,要想对学生进行数学思想方法的有效渗透,课堂教学中的三个关键环节不容忽视。

1.1 新知讲授前,应充分做好准备工作,深入钻研教材,制定适宜的教学目标,并研究本节课中所涉及到的数学思想方法有哪些,该怎样进行有效的渗透？只有做到了“胸中有成竹”,在付诸于实践时,才会有的放矢,从容、自如。

1.2 新知讲授时,应根据事先的计划,有步骤地进行数学思想方法的有效渗透。作为教师,应根据学生的思维认知特点,由浅入深、由易到难地让学生在实践操作或实际题目中感受到数学思想方法的存在,进而做到理解并掌握运用；应努力使学生做到依据数学思想选取适当的数学方法,在运用数学方法中发现所蕴含的数学思想。

1.3 新知讲授后,在组织复习巩固时,也应注重数学思想方法的有效渗透。学生对新知识的接受过程实际上是一个建构的过程,复习对于新知识的理解和掌握至关重要。我们教师教书,不仅要让学生知道学得了什么,更重要的是让学生懂得知识的来龙去脉,知道其中的缘由,乃至怎样去学会这方面的知识。所谓“不仅知其然,还要知其所以然”。“然”是什么？我想“然”便是其中所蕴含的数学思想方法。

2.注重多种数学思想方法的有效渗透

课堂教学,是包含着教师的教和学生的学的双边实践活动。而在这一活动过程中,会涉及到多种的数学思想方法。这就要求我们老师应当引导学生独立思考,积极探索,让学生的主体性得到充分的发挥,培养学生动手、动脑的能力,在教学中有效地渗透一些常见、基本的数学思想方法。在小学阶段,数学思想方法主要有符号化思想、数形结合思想、化归思想、推理思想、变换(转化)思想、分类思想、集合思想、极限思想、方程函数思想、模型思想、对应思想、统计与概率思想等等。下面我想联系自己的教学实践,针对以上的一些数学思想方法，谈谈我的一些具体做法。

2.1 数形结合思想方法和符号化思想方法的综合渗透。数与形是数学教学研究对象的两个侧面,把数量关系和空间形式结合起来去分析问题、解决问题,就是数形结合思想。“数形结合”可以借助简单的图形、符号和文字所作的示意图,促进学生形象思维和抽象思维的协调发展,沟通数学知识之间的联系,从复杂的数量关系中凸显最本质的特征。符号化思想主要指人们有意识地、普遍地运用符号去表述研究的对象。运用一套合适的符号,可以清晰、准确、简洁地表达数学思想、概念、方法和逻辑,避免日常语言的繁复、冗长或含混不清。这两者在我们的课堂教学过程中,常常紧密地联系在一起。

例如,我在教学《长方形的周长》一节内容时,是如此渗透的：

(1)问：什么是长方形的周长？

(2)画图示意(如右)，问：可以怎样计算？引导学生探索出不同算法：

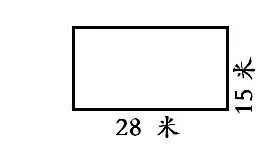
1)28+15+28+15=86(米);

2)28+28+15+15=86(米);

3)①28×2=56(米)，②15×2=30(米)，

③56+30=86(米);

4)①28+15=43(米)，②43×2=86(米)。

(3)让学生试比较四种方法的异同，并找出最优化的计算方法。

(4)请学生试用自己的语言叙述长方形周长的计算方法。适时启发学生：你会用文字关系式表达所叙述的计算方法吗？得出：(长+宽)×2=长方形的周长。

(5)告诉学生：可以用字母a表示长方形的长，用字母b表示长方形的宽，用字母c表示长方形的周长。问:可以用怎样的字母式表示长方形周长的计算方法？学生思考讨论后，口答：(a+b)×2=c。

本题教学过程中，我主要向学生渗透了两种数学思想方法，即数形结合的思想方法和符号化的思想方法。很显然，借助简单的示意图，可以使题目的条件、问题简明直观，具体形象。用字母表示长方形的计算公式既清晰准确又简单易记。

2.2 假设思想方法和推理思想方法的综合渗透。假设是先对题目中的已知条件或问题作出某种假设，然后按照题中的已知条件进行推算，根据数量出现的矛盾，加以适当调整，最后找到正确答案的一种思想方法。假设思想是一种有意义的想象思维，掌握之后可以使要解决的问题更形象、具体，从而丰富解题思路。推理是从一个或几个已有的判断得出另一个新判断的思维形式。推理所根据的判断叫前提,根据前提所得到的判断叫结论。推理分为两种形式：演绎推理和合情推理。在解决问题的过程中,合情推理有助于探索解决问题的思路,发现结论；演绎推理用于证明结论的正确性。在教学类似“鸡兔同笼”的问题时，我就主要向学生渗透了这两种思想方法。

例如：某次数学竞赛共20道题，评分标准是：每做对一题得5分，每做错或不做一题扣1分．小华参加了这次竞赛，得了64分．问：小华做对几道题？

教学时，我的做法是：

(1)师：我们可以假设这20道题全部都做对了，应该得多少分？怎样列式？学生：应该得100分，算式为20×5=100(分)。

(2)师：全部答对的结果显然是错误的，因为小华只得了64分，说明他肯定有答错或不答的题。请同学们思考：答错或不答一题损失几分？注意是损失！学生经过思考讨论后，答道：答错或不答一题损失6分，因为答错或不答一题，5分不但得不到了，还要被扣掉1分。算式为5+1=6(分)。

(3)师：我们假设20题全做对了得100分，实际结果只得了64分，相差了36分，算式为100-64=36(分)。答错或不答一题损失6分，请大家思考：算式36÷6表示什么意思？学生经过思考、讨论后，答道：表示答错或不答的题数。

(4)师：那么小华做对了几道题？请列出算式。学生：20-6=14(道)

(5)师：通过解决这道题，你有什么收获？还有别的解题方法吗？学生讨论后，独立完成。

(6)师：对于这类问题，你觉得可以怎样解答？说说你的方法。

显然，在上述的教学过程中，学生对假设思想方法和推理思想方法逐渐得到了渗透，特别是第6步的课堂总结，使学生对这两种思想方法有了进一步较清晰的认识。我个人认为，这种做法使学生解题有了新方法，扩宽了他们的解题思路。

2.3 渗透集合的思想方法。集合的数学思想方法是从某一角度看所研究的对象，使之成为合乎一定抽象要求的元素。在小学数学教学中，通常采用直观手段，利用画集合图的办法来渗透集合思想。

例如教学长方体、正方体之后，学生明白了正方体是长、宽、高分别相等的长方体，即正方体是一种特殊的长方体，这时我要求学生把“正方体”和“长方体”填在圆圈图(如右)内表示它们之间的关系。让他们感知大圈内的物体具有某种共同的属性，可以看作一个整体，这个整体就是一个集合——长方体集合，小圈内的物体也具有某种共同的属性，可以看作一个小整体，这个小整体就是一个小集合——正方体集合，使学生感受到长方体集合包含正方体集合。

以上仅是我的一些浅显做法，它们是我在课堂上对学生进行数学思想方法渗透的一些尝试和初探。在实际教学中，我个人认为需要深入钻研教材，努力挖掘教材中可以进行数学思想方法渗透的各种因素，把握好课堂教学中进行数学思想方法渗透的契机，根据儿童的心理特征、接受能力，采用相应的教学手段，使学生逐步掌握现代数学思想方法，从而发展他们的思维能力和创新能力。