基于社团结构的组合信息重连策略
2019-09-23刘三阳白艺光
张 姣,刘三阳,白艺光
(西安电子科技大学数学与统计学院,西安 710126)
0 引言



受到上述研究的启发,在本文中,我们提出了一种新的基于社团结构组合网络特征信息的链路重连策略,即CCLS策略。该策略在社团结构基础上,依据节点间的同配与异配程度和k-core结构对网络进行重连边。其分别在伪随机网络、CWS小世界网络、无标度社团网络以及真实网络上进行的仿真实验表明,它能有效地减弱网络社团特性,提高网络传输容量。
1 相关模型与参数
1.1 流量模型
假定:网络中的每个节点都有创建,接收和转发数据包的能力,并且每个节点的存储都是无限制的。每个时刻t,每个节点以概率ρ产生一个数据包,每个数据包随机选择与初始节点不同的目的节点,另外每个节点对数据包的处理能力都相同设置为C,新到达的数据包根据排队机制放在队列的末尾,不能及时处理的数据包排在队列末尾等候,节点依据First-in-First-out原则对数据包进行处理。数据包到达目的节点后就从网络中离开。
1.2 网络传输
当网络中节点产生数据包的概率ρ逐渐增加时,网络将由畅通逐渐变为拥塞。这个过程存在一个临界值ρc,当ρ<ρc时,网络产生的数据包小于节点的处理能力,数据包无堆积,网络畅通;当ρ>ρc时,网络产生的数据包超过节点的处理能力,数据包不能被及时传输而堆积,网络拥塞。为了准确描述从畅通状态到拥塞状态的临界点,可引入有序参数η与ρ的关系来分析网络变化。
(1)
其中,N为网络的节点个数,ΔW=W(t+Δt)-W(t),W(t)为t时刻网络中数据包的个数,〈ΔW〉表示对时间窗口Δt对应的ΔW求平均。当ρ<ρc时,ΔW=0和η=0,网络处于畅通状态;当ρ>ρc时,序参数变为正值,网络中的数据包发生堆积,网络处于拥塞状态。因此,可以用ρc来量化网络传输容量。
在网络畅通状态,任意节点vj接收到的数据包为ρBj/(N-1),其中Bj是节点vj的有效介数,定义如下:
(2)
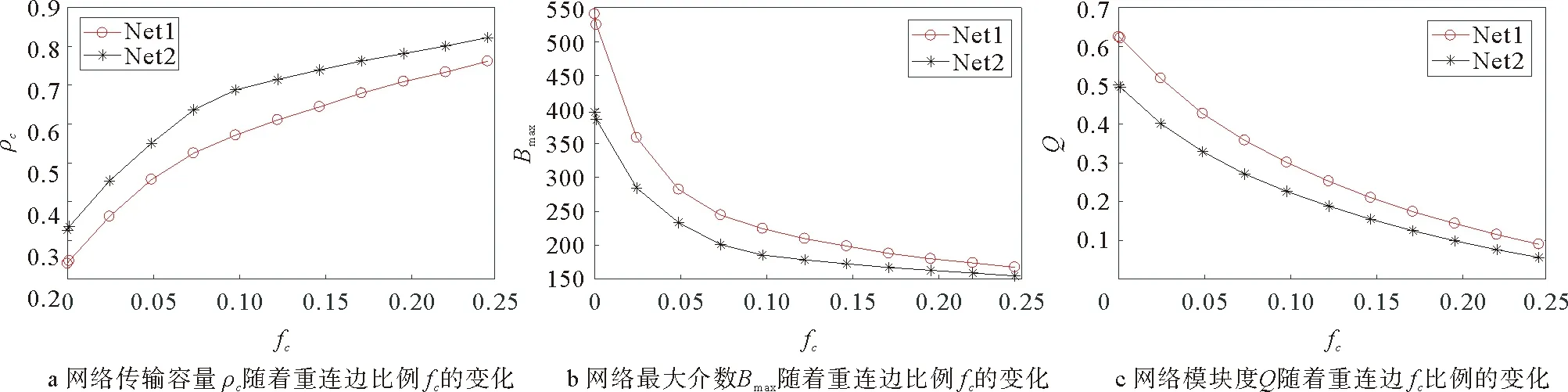
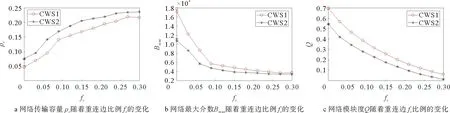
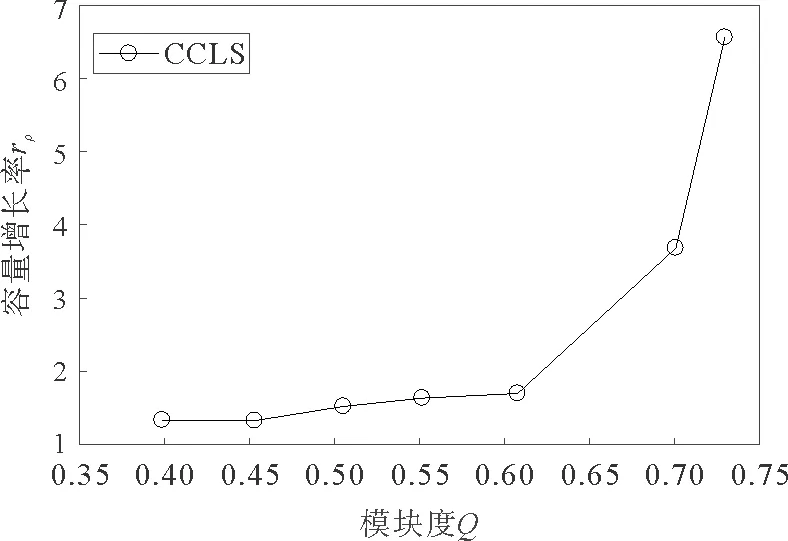
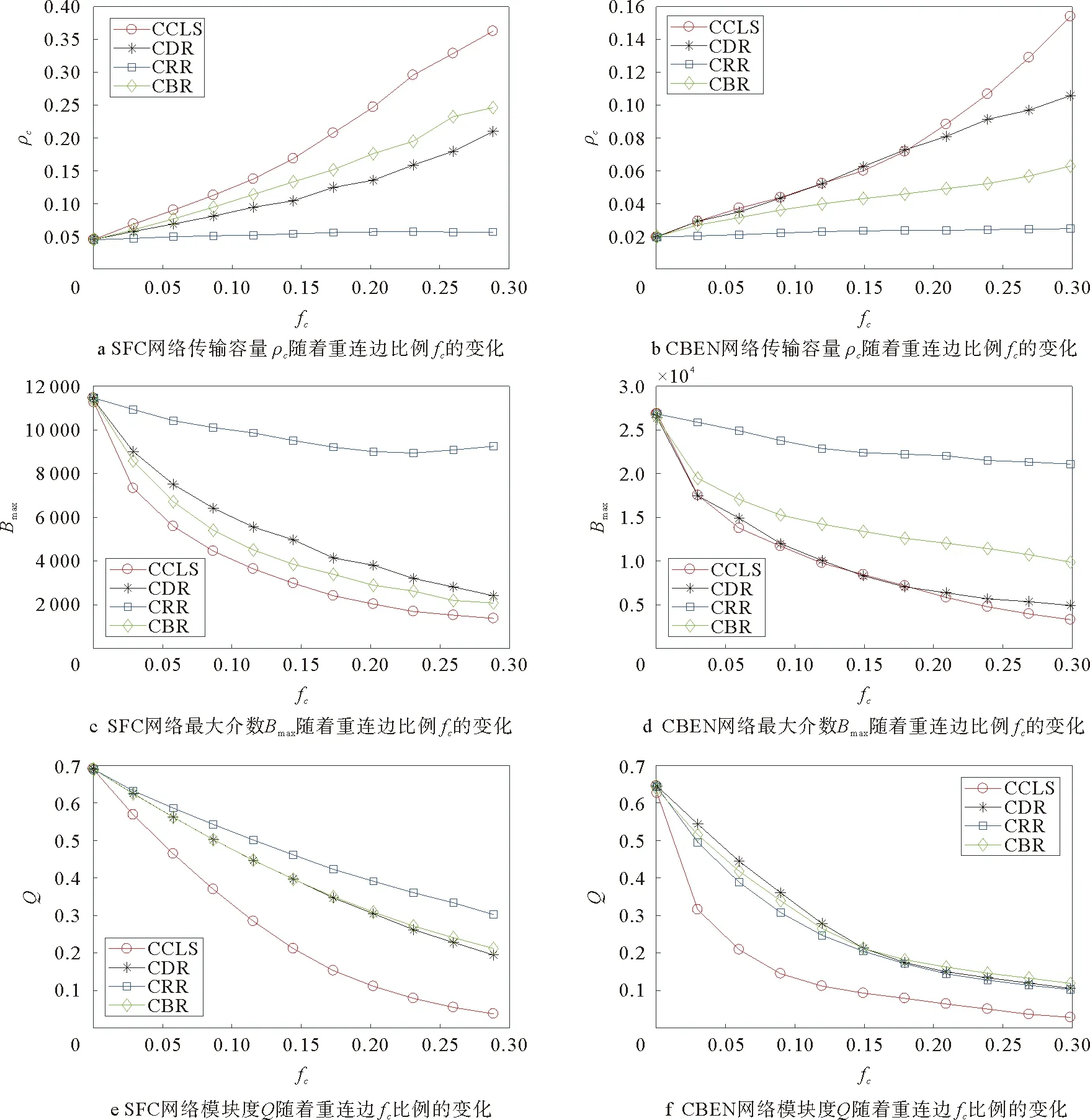
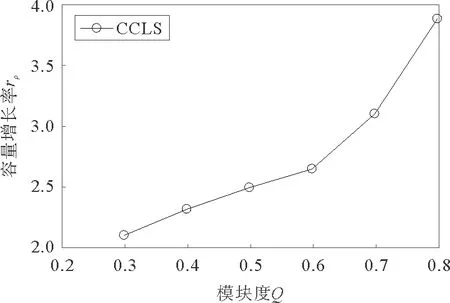
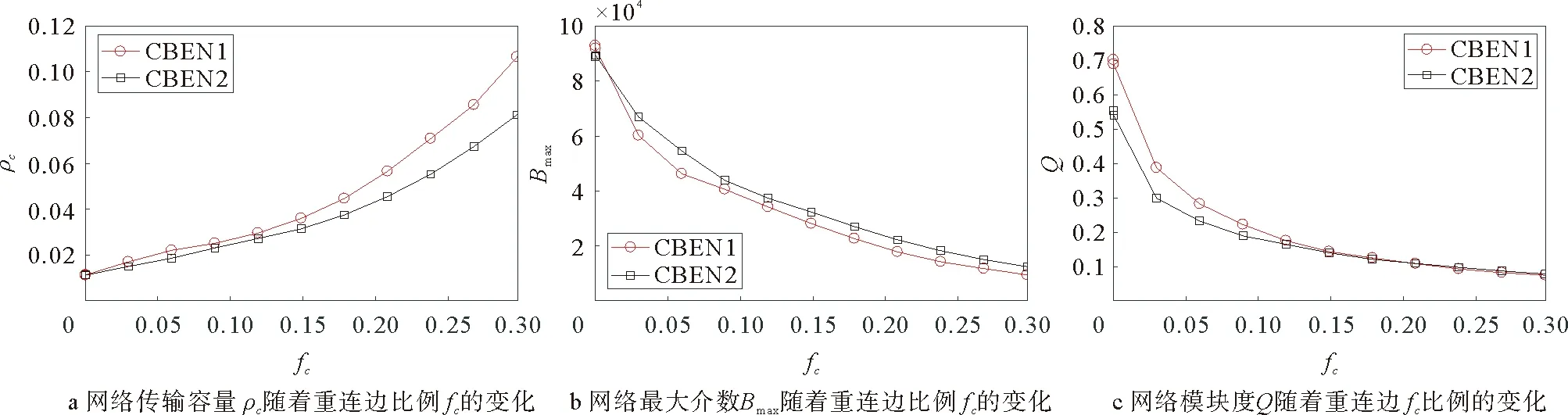
nil表示节点vi→vl的最短路径条数;nil(j)表示经过节点vj的vi→vl的最短路径的条数。如果ρBj/(N-1)>C,那么数据包将在节点vj上堆积,网络将会发生拥塞。因此,要想网络不发生拥塞,必须保证网络所有节点都不发生数据包堆积,即它们都满足ρBj/(N-1) (3) 其中,Bmax表示网络节点介数的最大值。 令C=1,网络传输容量ρc即为网络不发生拥塞的最大ρ值,可以用下边公式估计: ρc=(N-1)/Bmax (4) 社团是网络的一种中尺度结构,本文我们采用Newman等人提出的模块度Q来量化复杂网络社团结构的质量,把初始网络划分成k个社团,E=(eij)是k阶对称矩阵。模块度Q可以定义为: (5) 实际生活中多数网络具有明显的社团结构,且明显的社团结构不利于网络传输。因此,本文链路重连策略在对网络划分社团结构的基础上,利用节点间度度相关性,核心-外围结构等特征信息来模糊社团结构进而提高网络传输容量。 表1 算法1 需要注意的是每次删边和添边后,如果都重新对网络划分社团结构,计算量庞大,为简化计算,删除边时,若节点i与它所在的社团没有相连接的节点,对节点i按照社团对它的吸引力(吸引力是按照节点i与其他社团的连接度,度越大则吸引力越大)重新划分社团;添边时采用文章WCS策略[15]的命题3来重新规划节点u和v的社团归属。 在本文的链路重连策略中,要保证网络的连通性,如果删除一条边将导致某些节点断开连接,我们将不会将其删除并继续处理下一条边。重连边的比例被定义为:fc=mr/m,其中mr是重连边的数目,m是初始网络中的总边数。(本文的仿真结果数值都至少进行了20次独立重复实验) 在基于ER[23]模型生成的伪随机网络上分析CCLS策略对其传输性能的影响。该网络的产生方式如下:1)网络的节点数n=128,随机均分成4个社团。2)同一社团内两节点对以概率Pin连接,不同社团间两节点对以概率Pout连接。3)社团内部平均连接度为Zin,社团间平均连接度为Zout,且Zin+Zout=16。选择合适参数生成模块度Q=0.625和Q=0.5的网络,分别标记为Net1和Net2,Net2的社团特性比Net1的弱。应用CCLS策略,重连链路比例fc与网络传输容量ρc之间的关系如图1a所示,两个网络的传输容量ρc都得到提升。基于1.2(4)的分析,网络传输容量可以简化为ρc∝1/Bmax,因此,理论上网络的最大介数Bmax可以用来评估网络的传输能力。图1b显示了Bmax与重连链路比例fc的关系,由图可得,随着fc的增加,网络的最大介数Bmax在两个网络上都逐渐减小,这正说明网络负载传输能力在不断提升。由此可见,CCLS策略对伪随机网络的负载传输能力改善效果明显。最后图1c表明了网络模块度Q随着fc的增加在不断减小,说明CCLS策略能明显削弱网络的社团结构,a和c证实了模糊社团结构有利于网络负载容量传输。并且随着fc的增加,Net1网络ρc的提升以及Bmax和Q的下降都略快于Net2网络。因此,在伪随机网络上,CCLS策略能有效改善网络拥挤,提高网络传输容量,且对社团明显的Net1网络的改善效果稍稍优于Net2网络,但是效果不明显。 图1 在伪随机网络上,CCLS策略下ρcBmax以及Q与fc的关系Fig.1 On the pseudo-random network,ρcBmax and Q versus fc under the CCLS strategy CWS[24]模型构造算法:1)网络有N个节点,包含c个社团,初始时N/c个节点排成环,每个节点选择离它最近的K/2个节点连接,各社团首尾之间连接一条边;2)重连概率P=Pin+Pout,其中Pin表示社团内部重连概率,Pout表示社团之间重连概率;它们也分别表示社团内部重连边和社团间重连边的比例。 调整CWS模型的参数,分别生成Q=0.7和Q=0.55节点N=800的社团网络,分别标记为CWS1和CWS2。比较CCLS策略对两个社团网络CWS1和CWS2的影响,其中包括重连边比例fc分别与网络传输容量(ρc),网络节点的最大介数(Bmax)以及网络社团模块度(Q)的关系。从图2a、c可得,两个网络随着重连边比例fc的增加,网络传输容量ρc都在提升,模块度Q都在减小。由此可以说明,CCLS策略能有效模糊社团结构进而改善CWS网络的传输容量。从图2b最大介数Bmax的明显变化可看出,社团较强的CWS1网络的最大介数下降的快于CWS2网络,因此CCLS策略对社团较强的CWS1网络容量传输性能的改善效果略好于CWS2网络。 图2 在CWS网络上,CCLS策略下ρcBmax以及Q与fc的关系Fig.2 On the CWS network,ρcBmax and Q versus fc under the CCLS strategy 图3 CWS网络节点N=500,fc=0.15时,rρ与Q的关系Fig.3 rρ versus Q under the CWS network N=500 and fc=0.15 在基于BA模型生成的无标度社团SFC[25]和CBEN[26]网络上的分析:调整两个模型的参数,分别生成Q值为0.69的N=500的SFC网络和Q值为0.65的N=500的CBEN网络。将我们的链路重连策略CCLS分别和基于社团结构的其他3种链路重连策略进行比较,3种策略如下: 1)社团随机重连策略(CRR):在社团内部随机删除链路,社团间随机增加链路。 2)社团介数重连策略(CBR):在最大社团内删除高介数节点间的链路ω=Bi×Bj,增加最低介数节点与非其所在最大社团间的低介数节点间的链路ω=Bi×Bj。其中Bi,Bj分别表示节点i和j的介数。 3)社团度重连策略(CDR):在最大社团内删除高度节点间的链路ω=ki×kj,增加最低度节点与非其所在最大社团间的低度节点间的链路ω=ki×kj。其中ki,kj分别表示节点i和j的度。 ρc和Bmax与fc的关系如图4的a和b,c和d所示,随着重连边比例fc的提升,四种链路重连策略下,网络传输容量ρc都得到提高,分析其原因,CCLS,CBR,CDR策略下,根据无标度网络的社团特性,社团内节点聚集,边稠密,其内部Hub节点非常容易发生拥塞,因此,在社团内删除负载较重节点间的连边,那么许多数据包就不会到达这些Hub节点,前往非Hub节点,这样利用非Hub节点缓解了社团内Hub节点的拥塞。其次社团间的连边作为桥梁,到达的数据包较多,负载较重,因此造成拥塞的节点一般是这些桥梁的两端,我们在社团间选择负载较小的节点进行连边,利用这些连边,可以分担原始网络中社团间桥梁的负载,这样削弱了社团结构,同时提高了网络对数据包的传输能力。而CRR策略根据模糊社团结构有利于网络传输的特性,其在社团内删除链路,在社团间进行随机重连来削弱社团结构进而提高了网络传输容量。图4整体显示,随着fc的增加,这四种链路重连策略均能模糊社团结构来提高网络负载能力,并且当fc=0.25时,对SFC网络传输容量的改善能力CCLS>CBR>CDR>CRR;对CBEN网络传输容量的改善能力CCLS>CDR>CBR>CRR。 图4 在不同链路重连策略下ρcBmax以及Q与fc的关系Fig.4 ρcBmax and Q versus fc under different link rewiring strategies 图5 SFC网络节点N=500,fc=0.15时,rρ与Q的关系Fig.5 rρ versus Q under SFC network N=500 and fc=0.15 下面分析CCLS策略分别对不同模块度的SFC和CBEN网络传输容量的影响,如图5所示,SFC网络节点N=500,平均度k=14,调整其参数分别生成不同的模块度值Q,在重连边比例fc=0.15的情况下,我们发现社团结构越明显,CCLS策略对其传输容量的改善效果越好。 从图6我们分别生成Q=0.7(标记为CBEN1)和Q=0.55(标记为CBEN2)N=1 000的两个CBEN网络。利用CCLS策略,两个网络的传输容量ρc都得到提升,但是随着重连边比例fc的增加,CBEN1网络的ρc值提升快于CBEN2网络,并且CBEN1网络的Bmax的减少快于CBEN2网络,图6c显示,CCLS策略明显减弱了网络的社团结构,且社团结构越明显,减弱的也相对越快。因此,以上结果显示CCLS策略对社团特征相对较强的CBEN1的网络传输容量改善能力优于CBEN2。由此可见,在无标度社团网络中,网络社团结构越强,CCLS策略对网络传输性能的改善效果也相对越好。 图6 在CBEN网络上,CCLS策略下ρcBmax以及Q与fc的关系Fig.6 On the CBEN network,ρcB max and Q versus fc under the CCLS strategy 图7 在CCLS策略下ρc与fc的关系Fig.7 ρc versus fc under the CCLS strategy 最后在真实的US Air lines(来自于Pajek datasets)节点数332,边数2 126网络上的验证:在CCLS策略下,首先利用Newman的快速社团探测算法,把US Air lines划分为5个社团,网络传输容量ρc与重连边比例fc的关系如图7所示:可以看到随着重连边比例的增加,网络的传输容量在不断提升。 本文提出了一种通过削弱社团结构,社团内删除链路,社团间添加链路的重连策略即CCLS策略。分别在伪随机网络、CWS小世界网络、无标度等人造社团网络中进行了仿真实验,CCLS策略能有效抑制网络拥塞,进一步提高网络传输容量。在真实的网络中,如航空网络中通过本文策略,改变航线,提高了飞行的容量。因此,对于多数网络,本策略都具有较高的实用价值。1.3 社团划分的评价
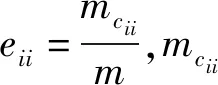
2 策略分析

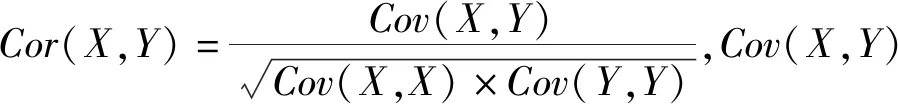


3 试验结果与分析
3.1 在伪随机网络中的验证
3.2 在CWS小世界网络中的验证

3.3 在无标度社团网络上的验证

4 结语
