基于高斯过程优化与FLAC3D数值计算的岩体力学参数反分析方法
2019-09-23龚杨凯12卢翠芳12黄杰12苏国韶12
龚杨凯12,卢翠芳12,黄杰12,苏国韶*12
(1.广西大学土木建筑工程学院, 广西南宁 530004;2.工程防灾与结构安全教育部重点实验室, 广西南宁530004)
0 引言
在地下工程稳定性分析中,由于岩体介质的高度复杂性和显著的尺度效应,室内及现场的岩石力学试验往往不能够合理地获得岩体力学参数,如何合理地确定岩体力学参数一直是一个比较棘手的现实问题[1]。利用岩体开挖过程监测到的位移或破坏区等实测信息进行反分析,进而推求定岩体参数的岩体参数分析方法是解决上述问题的有效途径。但是,对于复杂岩体工程,反分析的目标优化函数常具有表达式未知、高度非线性、多极值等特征[2],传统优化方法难以获取全局最优解。近年来,学者们采用的遗传算法(GA)、粒子群算法(PSO)、人工蜂群算法(ABC)等随机全局优化算法进行反分析,取得了良好成效[3-5]。但对于洞室群等大型岩体工程的参数反分析,为保证数值计算的精度,计算单元致密且数量庞大,导致单次数值计算的耗时较大,若采用随机全局优化算法进行反分析,常需要成千上万次地进行数值计算,因计算耗时巨大导致所谓的高计算代价问题。将机器学习模型与随机全局优化算法相结合是解决高计算代价问题的有效途径,利用机器学习模型替代数值计算模型,并建立岩体参数与数值计算结果的非线性映射关系,可显著提高计算效率,其中,基于神经网络—遗传算法(ANN-GA)以及支持向量机—遗传算法(SVM-GA)的反分析方法应用较为广泛[1、6-11],但这些方法尚存在着神经网络不适用于小样本、合理的网络结构与超参数难以确定、易限于局部最优解等局限性问题。
高斯过程优化(Gaussian Process Optimization, GPO)是近年出现的一种用于解决高计算代价问题的优化算法[12]。本文提出一种基于GPO的岩体参数反分析方法,为大型复杂地下工程岩体参数的合理确定提供一条新的途径。
1 GPO算法的基本原理
Efficient Global Optimization(EGO)算法源于1998年,是GPO算法的前身[12、13]。GPO的原理源于广泛应用于求解函数表达式未知的优化问题的贝叶斯优化方法[14-16]。GPO的基本思路是:利用少量训练样本建立回归模型,通过贝叶斯后验分布对待测区间进行概率预测,依据某种准则选取目标函数极值的预测最优解,将该解及其相应真实函数值作为新样本添入到训练样本中,在利用新训练样本集调整回归模型,不断重复此过程以获得全局最优解。它的基本实现步骤简述如下:
①根据少量训练样本建立高斯回归模型。
已知训练样本集(x,y),高斯过程回归模型为[17-18]:
y=f(x)+ε=xTw+ε,

n个训练样本的观察目标矢量y和1个测试样本的回归函数输出值f*所形成的联合高斯先验分布为:
式中:K(X,X*)是测试X*点与训练样本集合的所有输入点X的n×1阶协方差矩阵,k(X*,X*)是测试点X*本身的协方差矩阵,可分别简写为K(X*)、k(X*)。根据贝叶斯原理,给定新的输入X*、训练集的输入值X和观察目标值y的条件下,推断出f*预测值的均值和方差为:
②基于LCB准则获取预测最优点。
通过产生一个新的训练样本(预测最优解)提高回归效果。如何选择合理的新训练样本是GPO算法的核心问题。新样本的选择可通过对获取函数(Acquisition Function)的极值来获得,常用的获取函数有PI(Probability of Improvement)、EI(Expected of Improvement)、LCB(Lower Confidence Bounds)等三种[11],本文采用LCB准则:
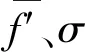
k=3-2.9×i/M,
其中:i为当前迭代步iter,M为最大迭代步Maxiter。αLCB(x)可采用优化算法求解,本文采用PSO算法。
③将预测最优解代入真实函数或者数值计算模型,获得一个新的训练样本,将此样本添入训练样本集。
④重复步骤①~③,直至满足收敛条件。
下面给出一个利用GPO算法求解一维多峰值函数最小值的示例,GPO采用SE协方差函数[10]。函数f(x)=xsin10πx+2-0.0516在[0, 0.9]区间的函数曲线见图1(a)。假设有5个初始训练样本(图1(a)),采用GPO进行寻优,仅经过6步迭代,就能迅速地获得全局最优解:x=0.7513,fmin=1.1977。
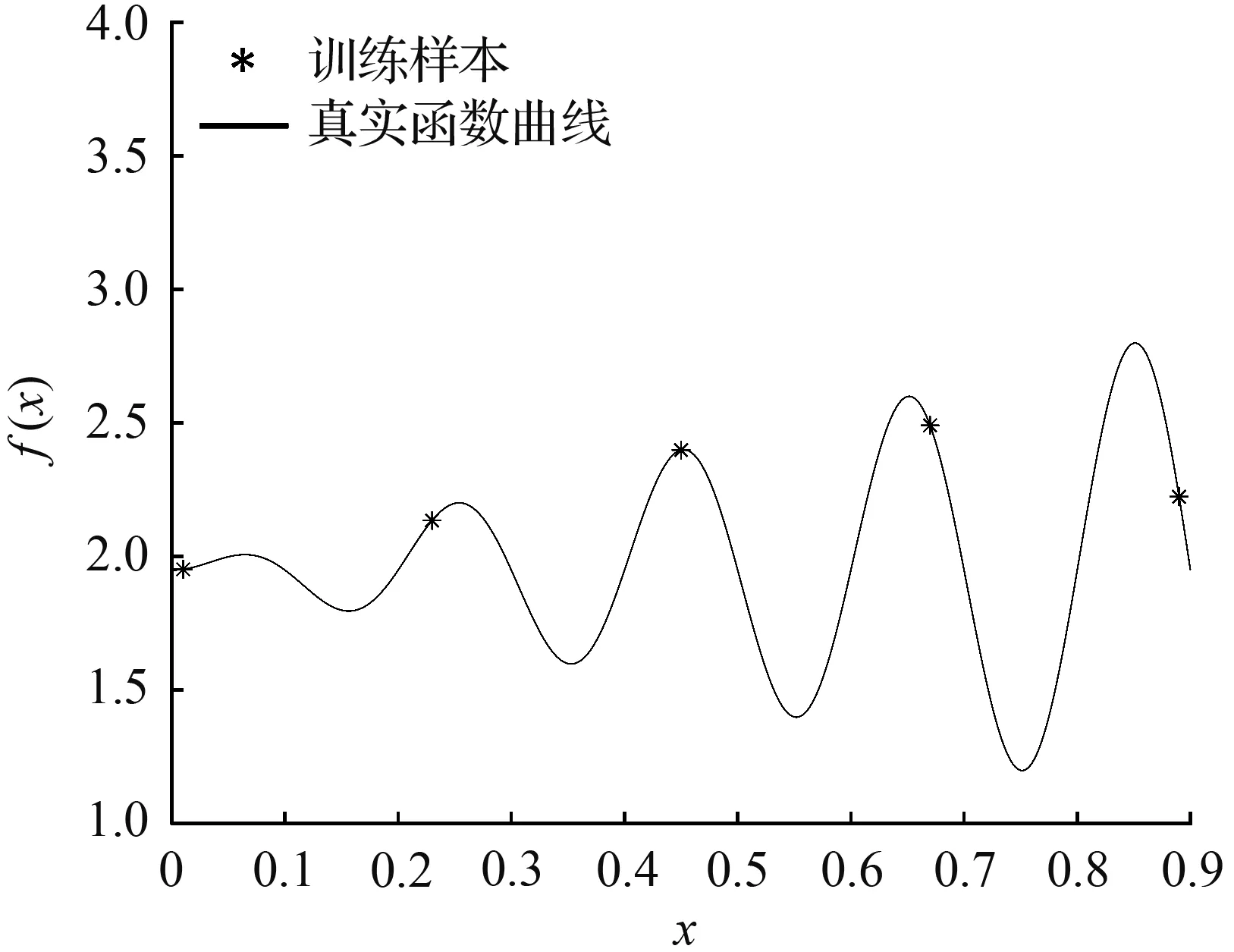
(a) 第0步
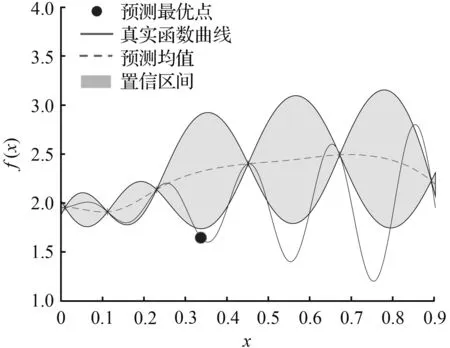
(b) 第2步
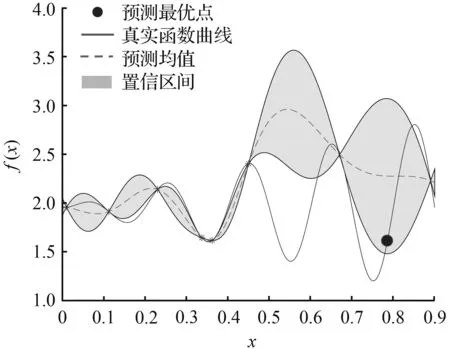
(c) 第4步
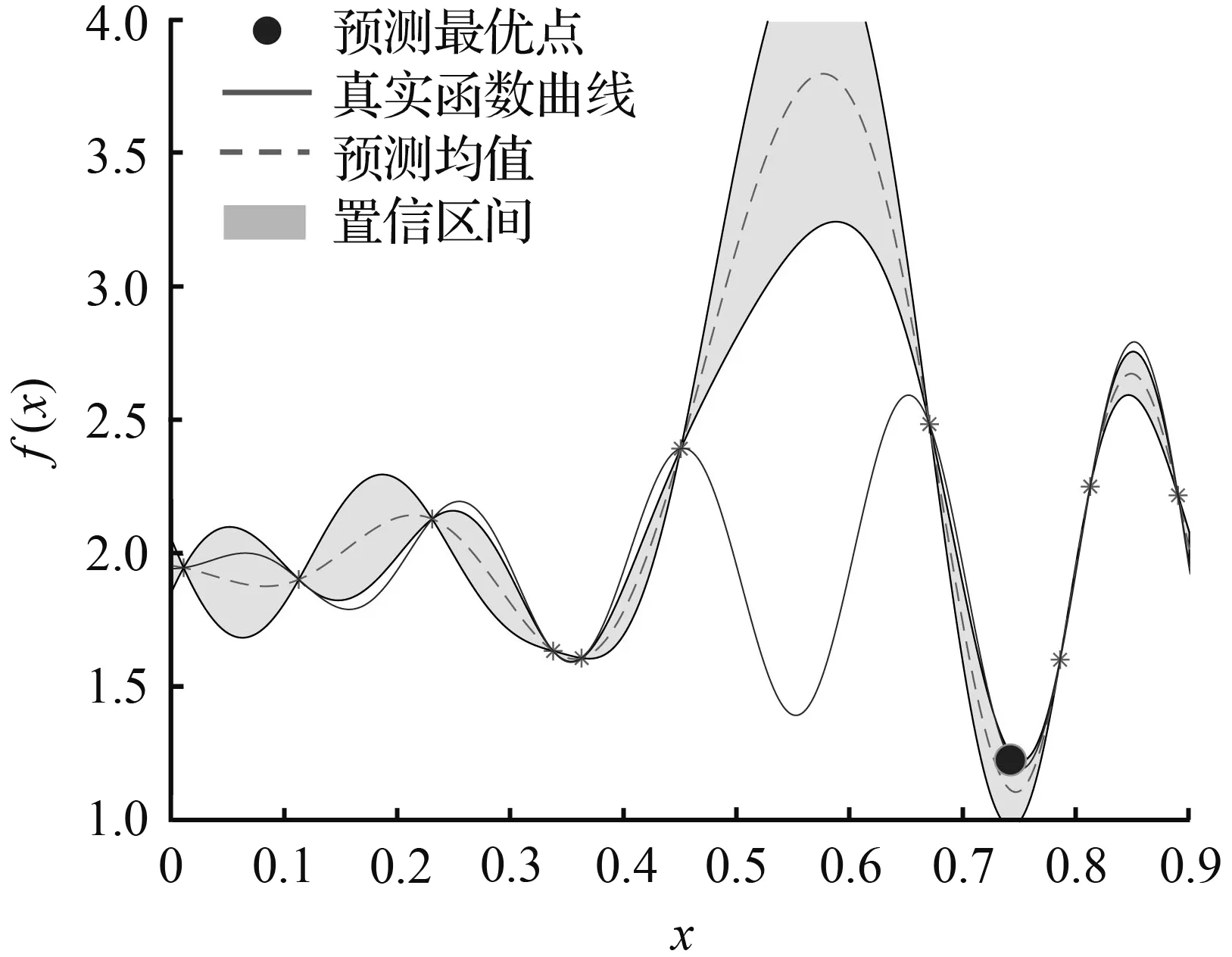
(d) 第6步
图1 一维函数的GPO寻优过程
Fig.1 An optimization processof one-dimensional function using GPO algorithm
2 GPO算法性能测试
为验证GPO算法的寻优性能,将它分别与随机全局优化法PSO、机器学习与随机全局优化算法相结合的优化算法GP-PSO[1]进行对比。函数极小化采用 Sphere(单峰非连续函数)、Schwefel(单峰连续函数)和Griewank(多峰连续函数)等三种常用的测试函数:
设优化问题维度n=5。为便于比较,PSO随机产生的初始样本作为GP-PSO、GPO的初始训练样本。f1(x)、f3(x)的收敛准则均为1×10-4,f2(x)的收敛准则为1×10-3。
三种算法中的PSO算法参数设置:学习因子c1=2.1、c2=2.0,最大速度Vmax=[1, 1, 1, 1, 1]。GP采用SE协方差函数。计算结果见表1,表中三种算法的计算结果为10次计算的均值。可见,与PSO相比,GP-PSO与GPO算法的函数调用次数降低了一个数量级;与GP-PSO相比,GPO的函数调用次数更少,例如,对于Schwefel函数,GPO通过22次实现收敛,比GP-PSO的函数调用次数少20 %。由此可见,GPO的优化效率更佳。

表1 三种算法的函数调用次数对比Tab.1 Comparison of the number of function calls among three algorithms
3 岩体参数反分析的GPO方法
对GPO算法编制MATLAB程序,利用MATLAB命令调用并打开FLAC3D数值计算软件,通过FLAC3D的fish内嵌语言编制数据接口文件读取岩体参数变量并进行数值计算获取围岩位移场,由此构建适应度函数表达式:
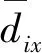

图2 高斯过程优化参数反分析方法的伪代码图
Fig.2 Pseudo code of parameter back analysis using GPO
4 工程算例
有一半径为3 m的圆形断面隧洞,水平和竖向初始地应力分别为15 MPa、10 MPa。假定岩体的本构模型为弹塑性模型,待反演的岩体力学参数分别为弹性模量E、粘聚力c和内摩擦角φ。为验证本文方法的可行性,假设岩体的“真实力学参数”为:E=2.2 GPa、c=4.0 MPa、φ=4×10°。将此参数代入FlAC3D数值计算模型(见图3,位移边界采用法向约束),计算其位移场,将开挖面上的1、2、3、4、5测点的位移计算值视为“实测位移”。为验证本文方法的先进性,分别采用PSO、GP-PSO与GPO三种方法进行岩体力学参数反分析。
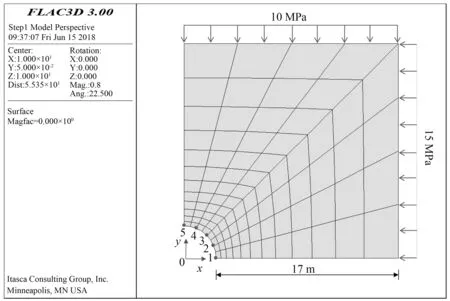
图3 隧洞的FLAC3D数值计算模型Fig.3 FLAC3D numerical model of the tunnel
PSO初始参数设置:c1=2.1、c2=2.0,最大速度Vmax=[1, 1, 1],寻优区间为:E=[1.0~4.0]GPa、c=[3.0~5.0]MPa、φ= [3~5]×10°。GP-PSO与GPO均采用SE协方差函数。为便于比较,三种方法的初始训练样本相同,见表2。
计算结果见表3。从中可知,当收敛准则设为f<0.3或数值计算最大次数300时,从数值计算次数来看,GPO分别为PSO、GP-PSO的14 %、60 %;从计算耗时来看,GPO分别为PSO、GP-PSO的16 %、58 %。当收敛准则为f<0.2时或数值计算最大次数200时,PSO算法无法收敛,GP-PSO的数值计算次数和计算耗时约为GPO的2倍。由此可见本文方法的先进性。

表2 初始训练样本Tab.2 Initial training samples

表3 三种方法的计算结果对比Tab.3 Comparison of the results of three methods
5 结论
本文提出一种基于GPO算法的岩体参数反分析方法。研究表明,本文方法是可行的,与基于PSO算法的反分析方法相比,本文方法的数值计算重分析次数显著减小,同时克服了PSO的计算代价较高、寻优结果波动较大的不足;与基于GP-PSO算法的反分析方法相比,本文方法的数值计算重分析次数有一定程度降低,更不容易陷入局部最优,且具有参数少、原理简单、实现容易等优点。因此,本文方法在解决大规模、高计算代价的岩体参数反分析问题上具有良好的发展潜力和应用前景。需指出的是,初始训练样本的建立对于寻优结果具有重要影响,关于如何生成高质量的初始训练样本是下一步需开展研究的课题。
