不同炮兵标准气象条件下决定射击诸元一致性分析
2019-09-23王兆胜
王兆胜
(陆军炮兵防空兵学院南京校区 火力系,江苏 南京 211132)
炮兵标准气象条件指为编拟炮兵射击用的射表,根据一年中平均的地面气温气压数据和气温气压随高度的变化规律,规定的一个接近大气平均状况的标准状态,它是一种人为的规定。利用射表决定射击开始诸元时,射击指挥员以射表数据为依据,根据阵地和目标的坐标、气象条件和弹道条件与标准射击条件的偏差,计算射击条件修正量,根据射击开始距离和方向查射表得到射击开始诸元。目前我国地面火炮射表编拟一般采用国内炮兵标准气象条件,一些外贸军品火炮根据需要,射表编制采用了北约国家炮兵标准气象条件,两者并不完全相同,相应地所得到的射表数据也有明显的差异[1-4]。射表数据的差异对射击开始诸元的一致性或对火炮的发射控制是否产生影响,笔者将对此进行研究。
1 两种炮兵标准气象条件对比
1.1 国内炮兵标准气象条件
国内炮兵标准气象条件为:无风,海拨0 m时地面气温15℃、气压1 000 hPa,相对湿度50%.
虚温τ随高度y的分布为[1-7]
y≤9 300 m:
τ=288.9-Gy;
(1)
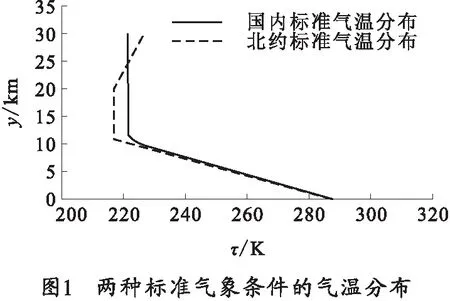
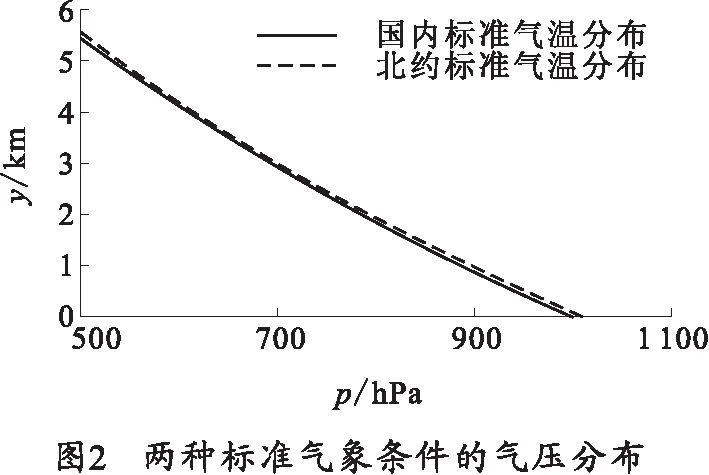
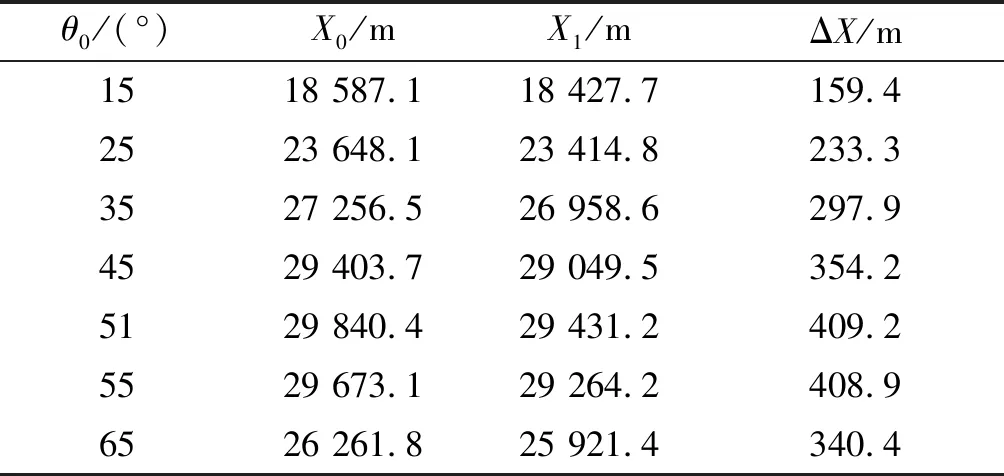
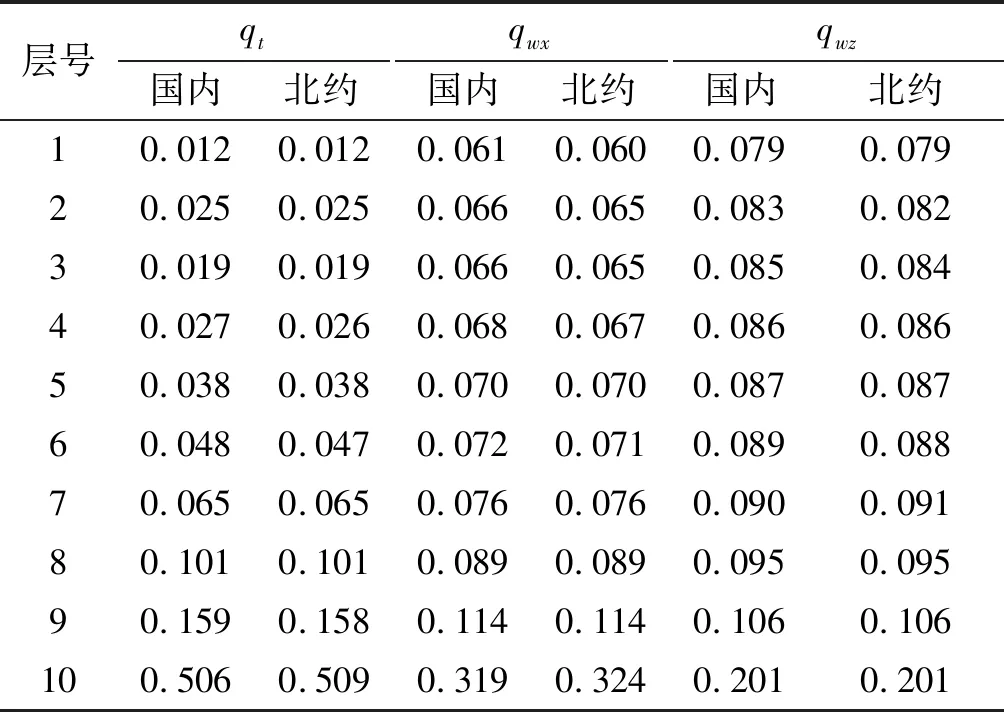
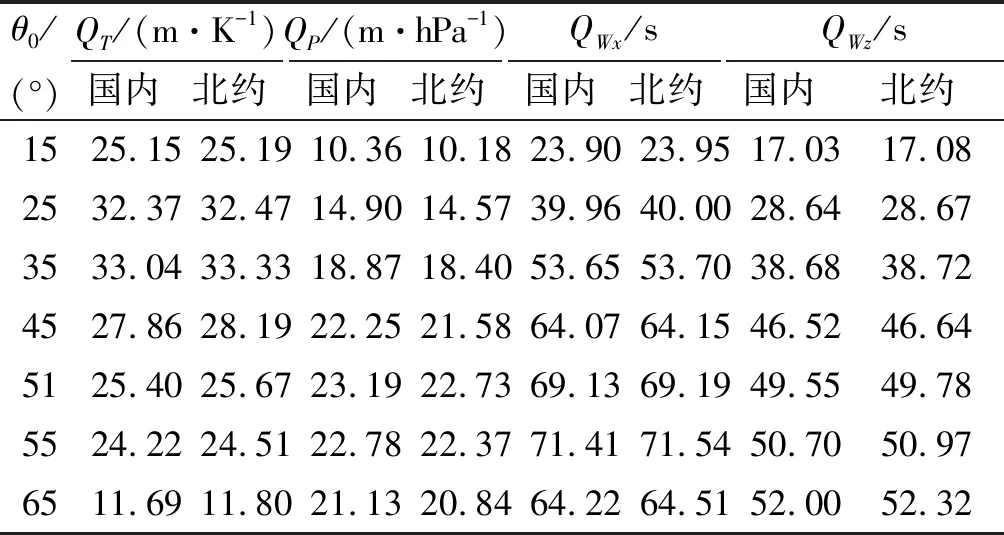
9 300 m τ=230.0-G(y-9 300)+B(y-9 300)2; (2) 12 000 m τ=221.5, (3) 式中:G=0.006 326;B=1.172×10-6. 根据虚温随高度的分布定律,可推出国内标准气象条件下气压随高度的分布。 北约炮兵标准气象条件为:无风,干空气,海拔0 m时地面气温15 ℃、气压1 013.25 hPa、空气密度1.225 kg/m3. 气温τ、气压p随高度y的分布为[6-7] y≤11 019.13 m: (4) 11 019.13 m (5) 20 062.85 m (6) 式中:P0=101 325 Pa;P1=22 632.05 Pa;P2=5 457.86 Pa. 对比两种炮兵标准气象条件,其差异主要有: 1)地面(海拔0 m)气象条件初值不同。国内标准气象条件的空气湿度为50%,因此地面虚温略大于气温;北约标准气象条件的空气为干空气,地面虚温等于气温,两者偏差0.75 K.另外,两者地面气压偏差13.25 hPa. 2)高空虚温有差异。两种标准气象条件的高空虚温分布差异如图1所示。从图1中可以看出,高度25 km以下时,国内标准的虚温大于北约标准的虚温。 3)两种标准气象条件的高空气压分布不同,高度6 km以下气压分布差异如图2所示。经计算,高度12 km以下,北约标准气压大于国内标准气压。 两种炮兵标准气象条件的差异将导致射表计算结果的不同。以最常用的三自由度弹道方程为例,标准气象条件下的射程X由弹道系数Cb、初速v0和射角θ0决定。设Cb=0.421,v0=930 m/s,分别取θ0为15°、25°、35°、45°、51°、55°、65°,以X0表示国内炮兵标准气象条件下的射程,X1表示北约炮兵标准气象条件下的射程,不同射角下X0、X1的计算结果及相应的ΔX=X0-X1如表1所示。 表1 两种标准气象条件下的射程 从表1所列的结果看,X0>X1,这是因为所计算的弹道上,相同高度的国内标准虚温较高,空气密度较低,阻力较小,因而射程较大。 弹道气象诸元偏差是将弹道上各高度实际气象诸元(气温、密度、纵风和横风)对标准气象诸元的不同偏差量等效处理成弹道各高度上都相同的气象诸元偏差量,以方便手工决定射击诸元时的气象诸元修正。从3个方面分析两种不同标准气象条件下的弹道气象诸元偏差。 准确地计算弹道气象诸元偏差量离不开精确的层权。精确层权与初速、射角等有关,一般通过弹道编程计算求出。在修正地面气压偏差和气温偏差方式下,气象诸元层权分为气温层权qt、纵风层权qwx和横风层权qwz.以v0=930 m/s为例,将θ0=45°的弹道均分为10个气层,表2为两种标准气象条件下各层精确层权计算结果。 表2 两种标准气象条件下的精确层权 从表2所列的计算结果看,尽管两种标准气象条件有差异,但气象诸元的精确层权基本相同。层权基本相同的意义是一般情形下只要按一种标准气象条件计算层权即可。 在修正地面气压偏差和气温偏差方式下,与气象条件修正有关的修正系数包括:气温偏差修正系数QT,为气温偏差1 K时的距离修正量;气压偏差修正系数QP,为地面气压偏差1 hPa时的距离修正量;纵风修正系数QWx,为纵风1 m/s时的修正量;横风修正系数QWz,为横风1 m/s时的修正量。v0=930 m/s,射角分别为15°、25°、35°、45°、51°、55°、65°时,两种标准气象条件下气象诸元修正系数的编程计算结果如表3所示。 表3 两种标准气象条件下的修正系数 从表3所列的计算结果看,尽管两种标准气象条件有差异,但气象诸元的修正系数基本相同。其意义是一般情形下只需按一种标准气象条件计算气象诸元修正系数即可。 在修正地面气压偏差与气温偏差方式下,弹道气象诸元偏差包括地面气压偏差,弹道温偏和弹道风。 设P0为国内标准气象条件下阵地的标准气压,P1为北约标准气象条件下阵地的标准气压,记 ΔPN=P0-P1. (7) 设P为阵地实测气压,ΔP0为国内标准气象条件下的阵地气压偏差,ΔP1为北约标准标准气象条件下的气压偏差,于是 ΔP0=P-P0, (8) ΔP1=P-P1=ΔP0+ΔPN. (9) 从式(7)~(9)可以看出,当国内标准气象条件下阵地气压偏差为ΔP0时,北约标准气象条件下的气压偏差为ΔP0+ΔPN. 设ΔTN为国内标准气温对北约标准气温的弹道温偏,ΔT0为国内标准气象条件下的弹道温偏,ΔT1为北约标准气象条件下的弹道温偏,则 (10) (11) (12) 式中:n为弹道分层数;qti为第i层的气温层权;τN0i为国内标准下第i层的标准气温;τN1i为北约标准下第i层的标准气温;τi为第i层的实际气温。 从式(10)~(12)可以看出,当国内标准气象条件的弹道温偏为ΔT0时,北约标准气象条件的弹道温偏为ΔT0+ΔTN. 设国内标准气象条件下的弹道纵风为Wx0,弹道横风为Wz0,北约标准气象条件下的弹道纵风为Wx1,弹道横风为Wz1,则 (13) 式中:n为弹道分层数;qwxi为第i层的纵风层权;qwzi为第i层的横风层权;wxi为第i层的纵风;wzi为第i层的横风。 由于两种标准气象条件下的纵风层权与横风层权基本相同,因此有 (14) 根据炮兵射击理论,对目标决定射击诸元的开始距离为 (15) 式中:DM为测地距离;ΔDM为射击条件的距离修正量。 (16) 开始方向为 (17) 式中:FM为测地方向;ΔFM为射击条件的方向修正量。 从式(17)看,开始方向由目标的测地方向和射击条件方向修正量组成,气象条件偏差对开始方向的影响主要是横风的影响。 取气象条件为北约标准气象条件,设阵地海拔为0 m,炮目距离DM=29 049.5 m,炮目高低角为0°,v0=930 m/s,Cb=0.421. 由于取的是北约标准气象条件,因此北约标准气象条件下气象诸元偏差量为0,即开始距离等于炮目距离,经过编程计算,得开始表尺为45°,即北约标准气象条件下的射角为45°. 对于国内炮兵标准气象条件而言,北约标准气象条件为非标准气象条件,其不仅存在地面气压的偏差,也存在气温偏差。 4.1.1 地面气压偏差修正 北约标准下海拔0 m的气压为1 013.25 hPa,相对于国内标准气象条件,地面气压偏差为ΔP0=13.25 hPa,v0=930 m/s,θ0=45°时气压偏差修正系数QP=22.25 m/hPa,因此气压偏差距离修正量ΔXP0为 ΔXp0=Qp·ΔP0=294.8 m. 因气压偏差为正,开始距离应加294.8 m. 4.1.2 气温偏差修正 v0=930 m/s,θ0=45°时,QT= 27.86 m/K.将弹道分为10层,采用精确层权计算的弹道温偏为ΔT0=-2.14 K,因此气温偏差距离修正量为 ΔXT0=QT·|ΔT0|=59.6 m. 由于温偏为负,开始距离应增加59.6 m. 4.1.3 开始距离与开始表尺 综合地面气压偏差修正量和气温偏差修正量,得开始距离为 29 049.5+294.8+59.6=29 403.9 m. 根据开始距离,经过编程计算,国内标准气象条件下的开始表尺为45°,即射角为45°. 该算例表明,取射击气象条件为北约标准气象条件时,尽管两种标准气象条件下的开始距离不同,但开始表尺相同,射击诸元具有一致性。 实际气象条件下的气象诸元偏差包括地面气压偏差、弹道温偏和弹道风。 设阵地海拨为0 m,炮目距离DM=20 km,炮目高低角为0,v0=930 m/s.根据炮兵弹道气象通报,国内标准气象条件下的阵地气压偏差为ΔP0=-10 hPa,弹道温偏为ΔT0=+5 K,弹道纵风Wx=8 m/s. v0=930 m/s,DM=20 km时国内标准气象条件下的射角为17.45°.气压偏差的修正系数为QP=11.6 m/hPa,气温偏差修正系数QT=27.56 m/K,纵风修正系数Qwx=28.04 s. 4.2.1 国内标准气象条件下的射击开始诸元 4.2.1.1 气压偏差修正 设国内标准下气压偏差距离修正量为ΔXP0,根据通报ΔP0=-10 hPa,偏差符号为“-”应减距离,于是 ΔXP0=QP·ΔP0=-116.0 m. 4.2.1.2 弹道气温偏差修正 设国内标准下气温偏差距离修正量为ΔXT0,根据通报ΔT0=+5 K,气温偏差符号为“+”应减距离,于是 ΔXT0=-QT·ΔT0=-137.8 m . 4.2.1.3 弹道纵风修正 设国内标准下纵风距离修正量为ΔXWx0,纵风为Wx=8 m/s,顺风时应减距离,于是 ΔXWx0=-QWx·ΔWx=-28.06×8=-224.5 m. 4.2.1.4 开始距离与开始表尺 综合以上气压偏差修正量、弹道气温偏差修正量和弹道纵风修正量,得开始距离为 20 000-116-137.8-224.5=19 521.7 m. 根据开始距离,经过编程计算,得国内标准气象条件下的开始表尺为 4.2.2 北约标准气象条件下的射击开始诸元 4.2.2.1 气压偏差修正 设北约标准下气压偏差距离修正量为ΔXP1,根据式(9)及ΔPN=-13.25 hPa,得ΔP1=-23.25 hPa,气压偏差符号为“-”应减距离,于是 ΔXP1=QP·ΔP1=-269.7 m . 4.2.2.2 弹道气温偏差修正 设北约标准下气温偏差距离修正量为ΔXT1,将弹道分为10层,经计算ΔTN=+0.98 K,根据式(12),得ΔT1=+5.98 K.温偏符号为“+”应减距离,因此 ΔXT1=-QT·ΔT1=-164.8 m. 4.2.2.3 弹道纵风修正 北约标准气象条件下纵风距离修正量ΔXWx1与ΔXWx0基本相同,即 ΔXWx1=ΔXWx0=-224.5 m. 4.2.2.4 开始距离与开始表尺 综合以上气压偏差修正量、弹道气温偏差修正量和弹道纵风修正量,可得到北约标准气象条件下的开始距离为 20 000-269.70-164.8-224.5=19 341.0 m. 根据开始距离,经过编程计算,得北约标准气象条件下的开始表尺为 以上算例表明,尽管不同标准气象条件下对目标的开始距离不同,但开始表尺相同,射击诸元具有一致性。 通过两种标准气象条件差异的对比,层权、修正系数等计算结果和算例分析,得到了如下的结论: 1)国内标准气象条件对北约标准气象条件地面虚温偏差较小,仅为0.75 K,地面气压偏差为-13.25 hPa. 2)初速与射角相同时,两种标准气象条件下的射程不同。 3)初速与射角相同时,两种标准气象条件下的气象诸元层权基本相同;气压偏差、气温偏差、纵、横风的修正系数基本相同。 4)当阵地对国内标准气象条件的地面气压偏差为ΔP0时,对北约标准气象条件的地面气压偏差为ΔP0+ΔPN.当实际气温对国内标准气象条件的弹道气温偏差为ΔT0时,对北约标准气象条件的弹道气温偏差为ΔT0+ΔTN.两种标准气象条件下的纵风与横风基本相同。 5)标准气象条件不同,决定诸元的开始距离并不相同,但并不影响决定射击诸元的一致性,标准气象条件的差异对火炮的发射控制没有显著的影响。1.2 北约炮兵标准气象条件
2 两种标准气象条件下的射程
3 弹道气象诸元偏差
3.1 层权
3.2 气象诸元偏差的修正系数
3.3 不同标准气象条件下弹道气象诸元偏差
4 决定射击诸元的一致性

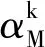
4.1 北约标准气象条件下的射击诸元一致性
4.2 实际气象条件下的射击诸元一致性
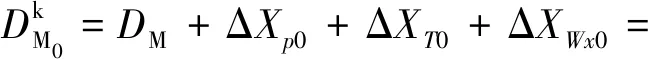
5 结论
