四元数Sylvester 方程的Toeplitz 约束解及其最佳逼近

黄敬频,蓝家新,毛利影,王 敏

(广西民族大学理学院, 广西南宁530006)

1 引言

Sylvester 方程是矩阵理论研究中非常重要的一类矩阵方程, 它在特征结构配置、航天控制技术、微分方程数值解、模式识别等领域都有实际应用[1−3]. 目前, 关于Sylvester 方程的解与约束解人们多在实数域或复数域上讨论, 并已取得丰富的成果[4−8], 而在四元数体上讨论该方程的约束解问题甚少. 随着四元数矩阵在图像处理、飞行器姿态控制等方面的应用发展[9,10], 讨论四元数Sylvester 方程的约束解具有较大实际意义. Toeplitz 矩阵是一类特殊结构矩阵, 它在信号压缩感知、超视距雷达电离层相位扰动校正等方面有重要作用[11−13].

本文目的是把实数域上的Sylvester 矩阵方程AX −XB = C 推广到四元数体上讨论,给出该方程存在Toeplitz 约束解的条件及解法, 同时讨论它的最佳逼近问题.

几年前，在外创业成功的柳中辉回村，村企联合进行新农村建设，打造总占地14000余亩的浔龙河生态艺术小镇。目前已投入140亿元打造文化产业、教育产业、康养产业、生态产业、旅游产业。

用Rn×n,Cn×n,Qn×n分别表示全体n 阶实矩阵、复矩阵及四元数矩阵集合;分别表示四元数矩阵A 的转置、共轭、共轭转置; A+表示A 的Moore-Penrose 广义逆;表示四元数矩阵A 的Frobenius 范数; vec(A) 表示矩阵A 按列顺序拉直向量; A ⊗B 表示矩阵A 与B 的Kronecker 积. 下面给出相关定义和引理.

定义1.1设T =(aij)n×n∈Qn×n, 如果满足aij=aj−i, 即

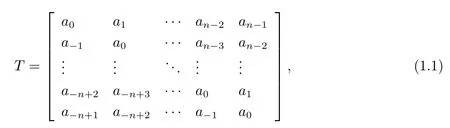
则称形如(1.1)式的矩阵为四元数Toeplitz 矩阵,全体n 阶四元数Toeplitz 矩阵记作TQn×n.

由于Xi∈Rn×n(i=0,1,2,3) 均是实Toeplitz 矩阵, 因此由引理1.1 可得

其中ei为单位矩阵In的第i 列. 易知Tn∈Rn2×(2n−1)是列正交的. 于是有

引理1.1设T =(aij)n×n∈Qn×n, 则

等价于

近日，杨女士因为连续几天便血，到医院做了肛肠检查，结果竟检查出肠道内有几颗大小不一的息肉，大的有豌豆大小。医生要求杨女士进一步进行肠镜检查，但是杨女士对再次做肠镜检查和内镜手术十分排斥，希望能够保守治疗。

设X ∈TQn×n, 它在实数域R 上的分解式为X = X0+ X1i + X2j + X3k, 其中Xi∈Rn×n(i=0,1,2,3) 均是实Toeplitz 矩阵. 又设A,B,C ∈Qn×n在实数域R 上的分解式为A=A0+A1i+A2j+A3k,B =B0+B1i+B2j+B3k,C =C0+C1i+C2j+C3k, 其中Ai,Bi,Ci∈Rn×n(i=0,1,2,3), 则四元数体上Sylvester 方程

本文主要讨论如下3 个问题.

据勘查，昌乐境内蓝宝石富矿区450平方公里，储量数十亿克拉，占全国蓝宝石总储量的90%以上，是继泰国、澳大利亚、斯里兰卡蓝宝石矿之后世界上发现的第四大蓝宝石矿床。昌乐蓝宝石化学成分和矿物成分与缅甸、泰国、柬埔寨、斯里兰卡等国家生产的蓝宝石并无大的不同，“其化学成分主要是三氧化二铝，就是金属铝的氧化物，因为含有微量元素钛和铁而呈现蓝色，并且具有颗粒大、颜色纯、质量好、双色性、易开采、奇异宝石多等特点。尤其是昌乐蓝宝石独有的双色性，即表面呈现蓝色，侧面则是神奇的绿色，颇受国内外珠宝界青睐，昌乐也因此被誉为“蓝宝石之都”。

问题I给定四元数矩阵A,B,C ∈Qn×n, 求矩阵X ∈TQn×n, 使得AX −XB =C.

问题II对给定的A,B,C ∈Qn×n, 求矩阵X ∈TQn×n, 使得||AX −XB −C||=min.

1.列举法。在教学中，以形符为纲，选取造字能力强的常用形符，以形符为中心展开教学。例如形符“木”，后面列举出“朴”、“机”、“杠”、“杖”、“村”、“材”、“枝”等由“木”这个形符构成的形声字。

问题III设问题I 的解集M ∈TQn×n是已知Toeplitz 矩阵, 求X 使得

2 问题I–II 的解

引理1.2[14]复数域上矩阵方程AX =C 有解的充要条件是AA+C =C. 此方程的通解和最小二乘解集均可表示为X = A+C +(I −A+A)Y, 其中Y ∈Cn×n是任意矩阵, 且存在唯一极小范数最小二乘解X0=A+C.

其中l(T),Tn分别如(1.2), (1.3) 式所示.

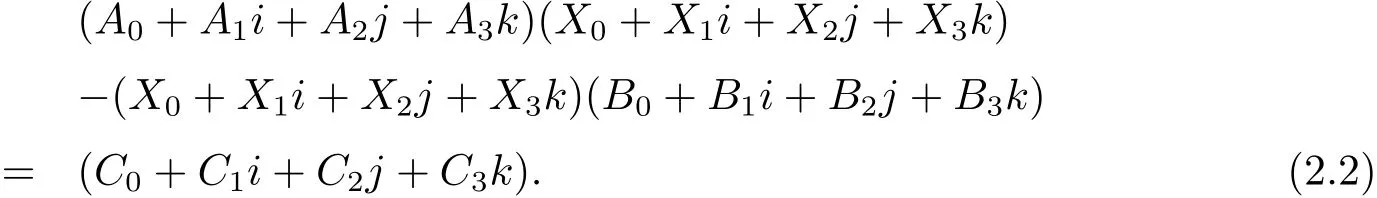
将(2.2) 式左边展开, 并根据四元数矩阵实分解的唯一性, 可得

信息化的发展和运用逐渐趋向成熟，各种信息化市场也逐渐趋向饱和。所以电信运营商信息化业务的竞争十分激烈。不断升级电信运营商内部的中心系统，采用先进硬盘零件，引进高科技技术。数据管理和监控要求企业采取统一化的管理方法，因为模式升级和系统升级是依赖于这两个因素的。信息化企业客户数量庞大，流失起来也很快。信息化企业可以利用这个特点进行客户的快速挑选，确认优质客户并且把客户流稳定下来，发掘更多的潜在客户渠道。信息化的企业还应该注意企业本身的业务水平，有意识提高自己的业务能力，增强自己企业的市场竞争力。

(2)圆上的任意一点到定点(圆心)的距离等于常数(半径)，而点M在椭圆上运动时，点F1、F2的位置不发生变化.请同学们用文字语言归纳,椭圆上任意一点应具有怎样的性质呢？

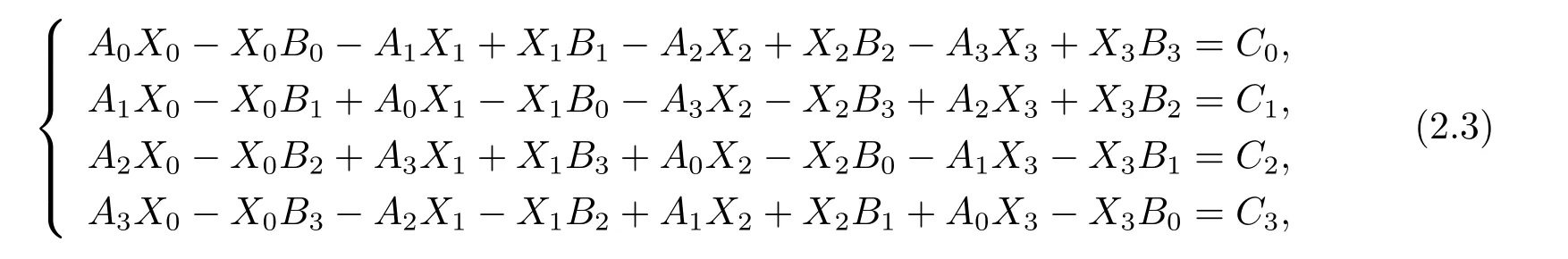
显然, 一个四元数Toeplitz 矩阵(1.1) 由它的第n 行和第n 列共2n −1 个元素唯一确定. 记

2.培养儿童思维和非智力因素的结合，有效弥补课堂过分强调智力训练的缺失。学习包含智力的训练和能力的培养，课堂文化的学习往往被认为是智力的训练。在培养学生智力和能力的过程中，不能忽视非智力因素的培养。如情感、意志、气质、性格等。非智力因素的良好培养是智力和能力发展的驱动。情境教学强调培养兴趣，着眼创造性，激发儿童情感，这正符合儿童非智力因素的培养要求。

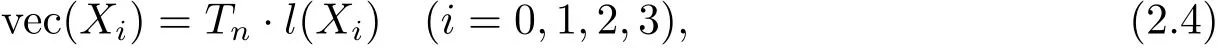
其中Tn如(1.3) 式所示. 记

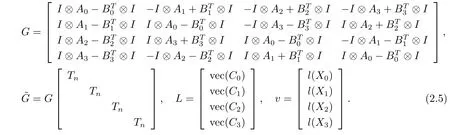
由于(2.4) 式等价于

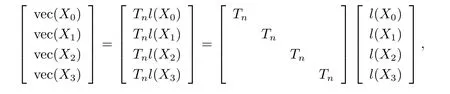
因此方程组(2.3) 等价于

第三,外源性与内源性病原体所致盆腔炎,上述两种病原菌也单独存在,也可一并存在,病情较复杂一般需联合用药。

此外, 利用矩阵Frobenius 范数可得

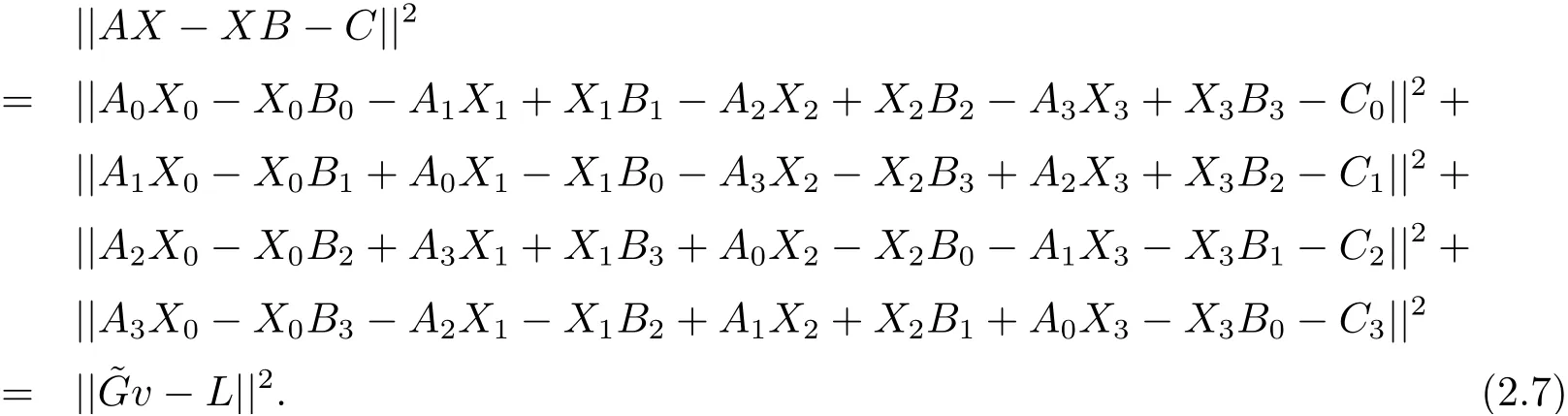
于是, 关于问题I–II 的解, 有如下的结果.

证当X ∈SE时, 根据定理2.1 及(3.2) 式可知||X −M||2= min其中是一个正对角矩阵. 当, 由引理1.2, 上式关于Y 的最小二乘解为(2.1) 存在唯一解因此不论哪种情况均有

低碳经济推动着会计理念改革，而会计理念改革也将加快全球低碳经济化的形成。为了紧跟低碳经济发展脚步，电力企业财务工作者必须改革传统的会计管理理念以及操作技术。站在全面客观的角度，综合考虑企业低碳排放在市场需求与能源成本之间的关系，特别是在市场准入、税收政策、金融支持等方面的影响。

其中这里的符号意义与前面所示相同.

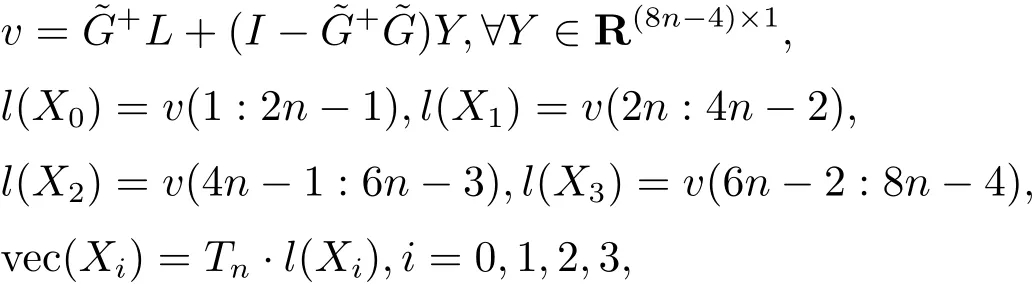
证由方程组(2.6) 及引理1.2 可得, 方程组(2.1) 存在四元数Toeplitz 解⇔方程组(2.6)有解=L. 有解时, (2.1) 的Toeplitz 解显然由(2.8) 式给出. 无解时, 由(2.7) 式可得= min ⇔= min. 因此(2.1) 式的最小二乘Toeplitz 解仍为(2.8) 式. 证毕.

3 问题III 的解

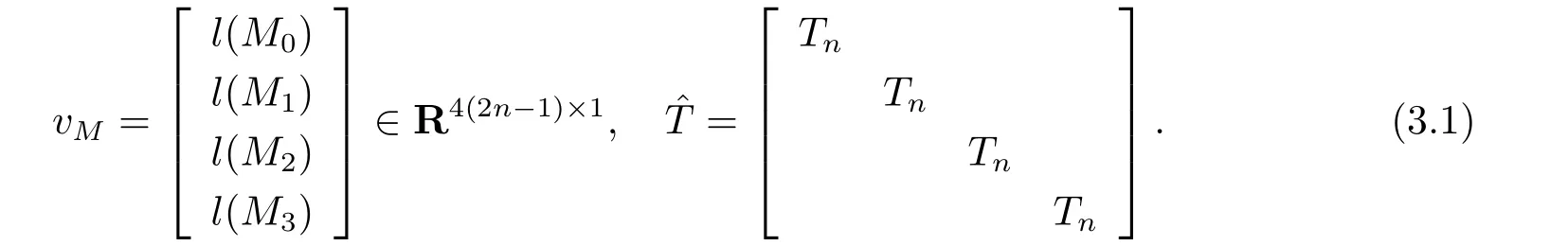
则有

其中

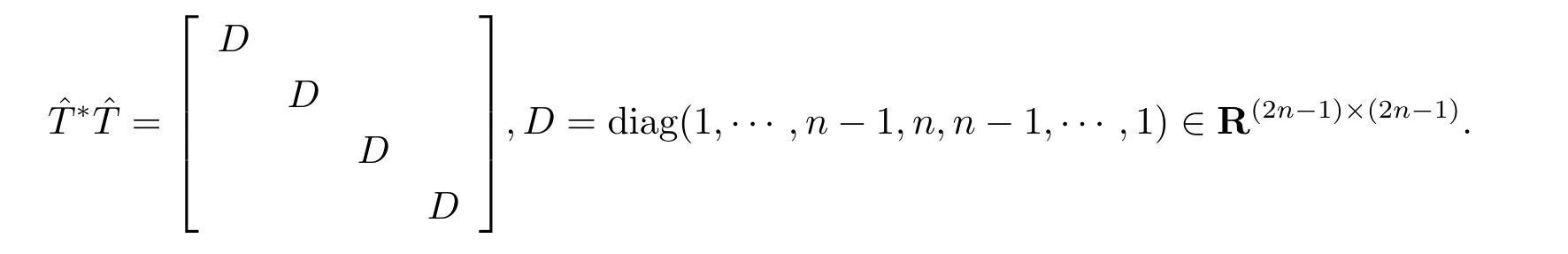
于是关于问题III, 有如下结果.

定理3.1设问题I 的解集是已知四元数Toeplitz 矩阵, 则在SE中使得=min 的解存在, 且有如下表达式

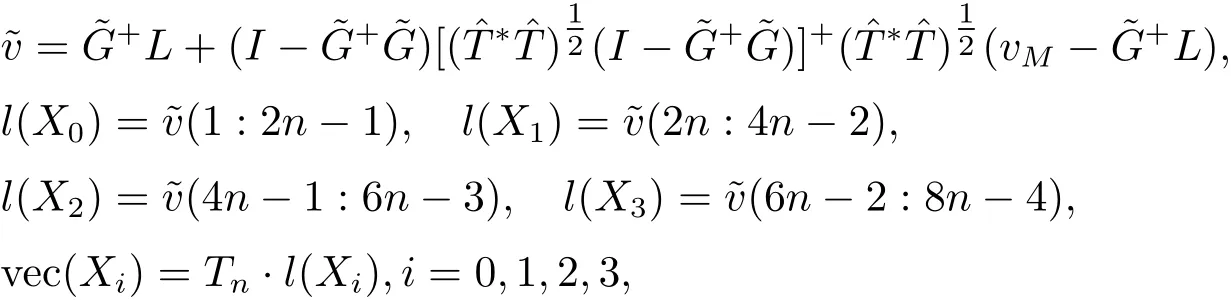
无解时, 它的最小二乘Toeplitz 解仍为(2.8) 式, 其中

80后女诗人，作品先后发表于《青年文学》《大鹏湾》《衡阳日报》《衡阳晚报》等报刊杂志。2006年至今坚持在网上写了数百首诗歌，并引起关注。诗歌《每天吃一点毒药》曾获2006-2007年网络文学节诗歌三等奖。

定理2.1给定四元数矩阵A,B,C ∈Qn×n, 则Sylvester 方程(2.1) 存在四元数Toeplitz解的充要条件是˜G ˜G+L=L. 有解时, 它的一般Toeplitz 解为

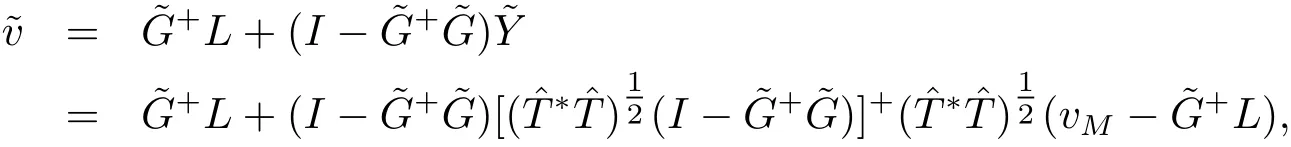
Nif、CsA因价格低廉、临床疗效好，已成为临床上治疗高血压、心绞痛和器官移植术后常规服用药物。有研究显示，Nif、CsA均会引起牙龈增生，尤其当两种药物联合应用时，牙龈增生也明显加重[5]，影响患者的咀嚼功能和牙周组织的健康。目前，药物性牙龈增生的具体发病机制尚不清楚，多认为是成纤维细胞增殖活性增强和(或)凋亡受到抑制，进而促进成纤维细胞的活性[12],导致胶原纤维合成与分解代谢失衡，引起以胶原纤维为主的细胞外基质(Extracellular matrix，ECM)的大量聚积[8]，从而导致了牙龈的纤维性增生。

根据定理2.1 和定理3.1, 我们给出问题I–III 的求解步骤:

步1写出四元数矩阵A,B,C 的实分解式, 即A = A0+A1i+A2j +A3k,B = B0+B1i+B2j+B3k,C =C0+C1i+C2j+C3k.

步2按(2.5) 式写出实矩阵˜G 和实向量L.

步3检验条件˜G ˜G+L=L 是否成立.

i) 若条件成立, 说明问题I 有解, 并按(2.8) 式写出其Toeplitz 解集SE;

ii) 若条件不成立, 说明问题I 无解, 此时问题II 的最小二乘Toeplitz 解集仍为SE.

两组的生活质量、满意度评分进行比较,观察组的生活质量、满意度评分高于对照组,统计学有意义(P<0.05);见表2。

步4在问题I 有解时, 对给定的四元数Toeplitz 矩阵M, 按(3.1) 式写出对应的实向量vM.

目前,海上风电主要采用长距离海底交流电缆传输的方式进行传输。相比陆上的架空线路,海底交流电缆的容性充电功率较大,随着离岸距离的增加,可能导致并网点以及所接入区域电网的节点出现过电压,同时也会增加电网内部的网络损耗。因此,对于大规模海上风电场所接入的区域电网,研究其无功电压优化问题,以提高节点电压质量和减小网络损耗,是海上风电并网研究的重要课题之一[1-3]。

步5按(3.3) 式写出问题III 的最佳逼近解˜X, 即由vec(Xi) = Tn·l(Xi),i = 0,1,2,3,可得出4 个实Toeplitz 矩阵Xi,i=0,1,2,3, 从而获得˜X =X0+X1i+X2j+X3k.

4 数值算例

算例给定下列四元数矩阵

试讨论Sylvester 方程(2.1) 的Toeplitz 解的存在性.

解四元数矩阵A,B,C 的实分解矩阵分别为

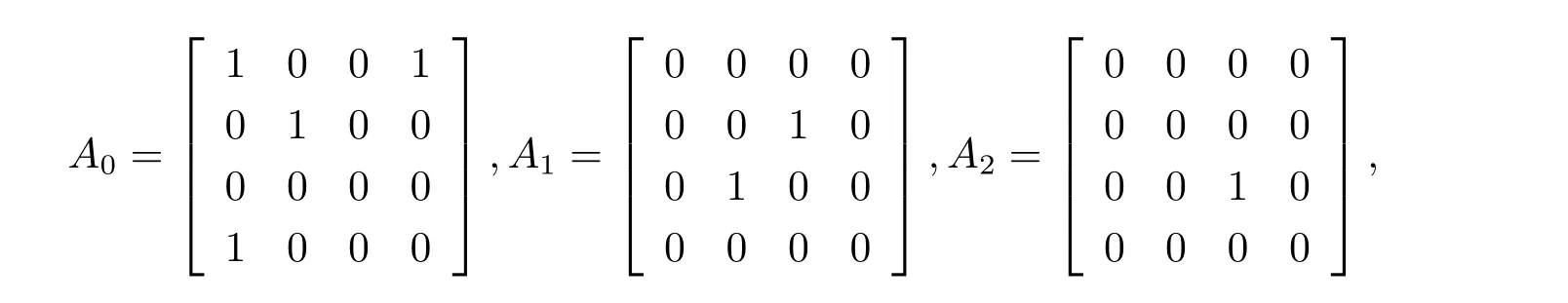
5 结语

本文提出一种判断四元数Sylvester 方程是否具有Toeplitz 约束解的方法. 我们根据Toeplitz 矩阵的结构特点, 给出四元数Toeplitz 矩阵的新刻划. 利用四元数矩阵的实分解和矩阵的Kronecker 积, 把约束方程问题转化为无约束方程问题, 解决了四元数乘法非交换的限制, 得到了四元数Sylvester 方程具有Toeplitz 解的充要条件, 以及它的Toeplitz 解集和最小二乘解集SE. 此外, 利用矩阵Frobenius 范数性质, 在Toeplitz 解集的条件下, 获得SE与预先给定的四元数Toeplitz 矩阵M 有极小Frobenius 范数的最佳逼近解. 本文结果可为解决相关约束四元数矩阵方程问题提供有益参考.