加权Laplace 在积分Ricci 曲率条件下的特征值估计

侯标

(武汉大学数学与统计学院,湖北武汉430072)

1 引言

特征值问题是几何分析的一个重要研究课题,且在偏微分方程以及物理学科有着广泛的应用. 其中关于黎曼流形上Laplace 算子第一特征值的估计问题,就已经得到许多重要的结果.Lichnerowicz[1]首先得到了紧致无边流形在满足Ric≥(n −1)K(K > 0)的Laplace 算子的第一特征值估计.进一步地, Li-Yau[2]利用梯度估计的方法考虑了, 完备流形M 本身Ric> 0的情况, 得到了Laplace 算子的第一非零特征值估计. 然而, 这个估计并不是最优的. 1984 Zhong-Yang[3]给出了这种情形下的最优估计. 同样地, 在考虑带边的黎曼流形时, 1980 年,Li-Yau[2]证明了紧致带边流形M Ric≥0 ∂M 是凸的情况下,Neumann 边值条件下Laplace 算子的第一非零特征值估计.其他边值条件下相应的特征值估计问题也得到了(参考文献[4]).

当Laplace 算子推广到加权Laplace 算子时,加权Laplace 算子第一非零特征值也逐步被得到. 加权Laplace,定义为

其中Φ 是流形Mk的函数. 它是L2(M,dµ)上的一个自伴随算子. 称λ 是加权Laplace 算子∆Φ的特征值是指如果存在一个非零的函数u ∈C∞(M)满足

一般的,在这种情形下需要引入新的曲率条件,m-Bakry-´Emery Ricci 曲率

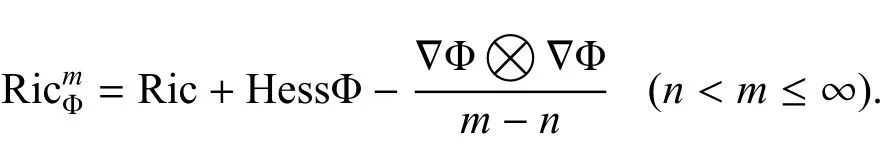
对于紧致无边的黎曼流形或者紧致带有凸边界的黎曼流形上加权Laplace 的第一非零特征值问题,Bakry-Qian[7]得到了一个在流形m-Bakry-´Emery Ricci 曲率有下界情形下第一特征值的统一的下界. 受到最近关于Ricci 孤立子和自收缩子研究的启发,通过假定光滑度量测度空间m-Bakry-´Emery Ricci 曲率,得到了许多关于加权Laplace 算子的梯度估计和特征值估计的结果.更多结果可以参考文献[8–10]以及它们的引用.

最近,在假定流形积分Ricci 曲率有界的条件,Wei[11]证明了一类紧致无边流形上Laplace算子的第一非零特征值的下界估计.

受到上述工作的启发,我们考虑了在光滑度量测度空间(M,g,dµ)上,当积分Ricci 曲率有界时,加权Laplace 算子的第一非零特征值的估计问题.通过运用Bochner 公式和加权Reilly公式[12],我们首先得到了完备无边流形加权Laplace 算子的第一非零特征值的下界估计.

定理1(Lichonerowicz-Obata 型估计)令(M,g,dµ)为一个光滑度量测度空间,其中(M,g)为n 维完备无边的黎曼流形, dµ = e−Φdv, Φ 是流形M 上的光滑函数. 对任意的q >以及K >0,都存在使得如果则加权Laplace 的第一非零特征值λ1满足

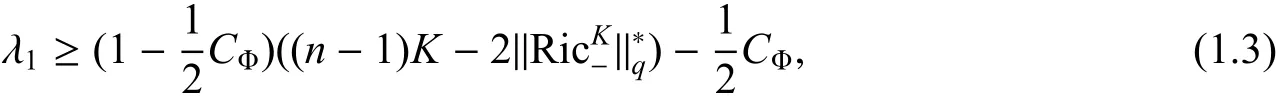
其中CΦ=max这里要求

推论1特别地,当RicM≥(n −1)K,Φ=0,有

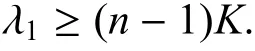
这刚好是对应的流形上的Lichonerowicz-Obata 型估计.

推论2当流形M 上的函数Φ 为常函数时, 此时对应的结果刚好是文献[11] 在研究p-Laplace 算子时p=2 的情形.

我们还得到了度量测度空间在流形本身带有边界的情形. 为了定理的叙述,还需要一些概念. 令v 表示∂M 的单位外法向量场,∂M 的第二基本形式定义为II(X,Y)=对任意的∂M 的向量场X 和Y,定义

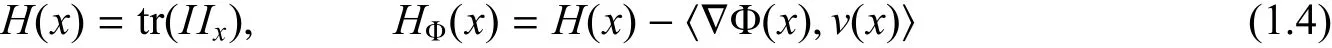
为在x ∈M 上的平均曲率和加权平均曲率. 称∂M 是凸的如果第二基本形式II ≥0. 如果假设Dirichlet 边界条件u = 0 或者Neumann 边界条件= 0. 相应地,分别用λD和λN表示加权Laplace 第一非零Dirichlet 特征值和第一非零Neumann 特征值.

定理2令(M,g,dµ)为一个光滑度量测度空间,其中(M,g)为n 维紧致带边的黎曼流形,dµ=e−Φdv,Φ 是流形M 上的光滑函数. 对任意的q>以及K >0,都存在使得如果<以及

(1) 如果∂M 上的加权平均曲率H −Φv是非负的,则第一非零Dirichlet 特征值λD满足

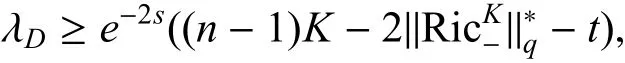
(2) 如果∂M 是凸的,也就就是说,第二基本形式(定义为h(X,Y) = g(∇Xv,Y))是非负的,则第一非零Neumann 特征值λN满足

同时,由于带边流形上也有Rielly 公式,自然可以考虑到超曲面情形. 通过定义, M 上的一个极小的Φ-超曲面P 是指一个超曲面P 满足H −Φv= 0,其中v 是定义在P 上第二基本形式的单位外法向量. 用∆P表示P 内度量的Laplace 算子,表示P 内度量的加权Laplace算子,那么得到

定理3(Choi-Wang 型估计)令(M,g,dµ)为一个光滑度量测度空间,其中(M,g)为n 维闭的可定向的黎曼流形, dµ = e−Φdv, Φ 是流形M 上的光滑函数. 令P ⊂M 为一个嵌入的极小Φ - 超曲面把M 分成2 个子流形M1和M2(i.e., H = Φv, 这个等式不依赖于单位法向v). 对任意以及K > 0, 都存在和使得M1M2满足如果则对于加权Laplace,在P 上的第一非零特征值λ1满足

推论3当取Φ 为常函数以及时= 0,= 0 时, 这个就是对经典的Choi-Wang 的结果.

推论4这个也是对Li-Sheng 等人工作的推广,详细可参考文献[12].

2 预备知识

我们准备介绍一下积分曲率条件.对每一个x ∈Mn,让ρ(x)表示Ric 张量的最小的特征值Ric:TxM →TxM. 令

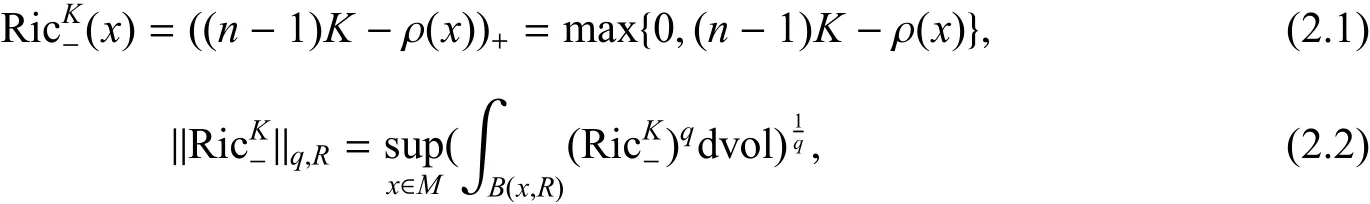
3 定理证明

首先给出一个引理.

引理1给定任意的以及K >0,都存在一个=(n,q,K)使得Mn是一个完备黎曼流形满足,则存在一个依赖于n,q,K 常数Cs(n,q,K)使得

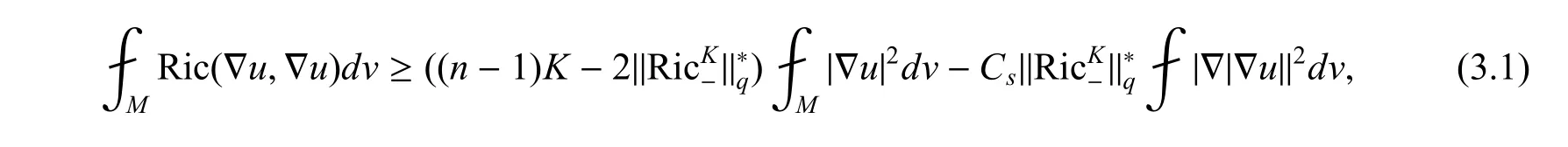
对所有的函数u ∈W1,2.

为了引理证明,需要给出2 个命题.

命题1(Aubty 直径估计[13])令(Mn,g)为n 维的完备黎曼流形以及. 如果存在一个C(p,n)使得其中C(p,n)表示仅依赖于p 和n 的常数,则流形M 是紧致的且有

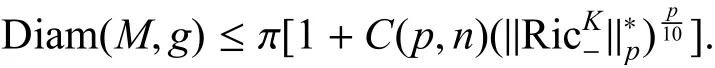
注1这个命题不仅告诉只要积分Ricci 曲率有界,就一定能保证流形M 本身是紧致的.更为重要的是,它给出了在积分Ricci 条件下流形本身的直径与曲率的关系,建立了流形上拓扑性质与几何条件的联系.

命题2(Gallot 等周常数估计[14]) 给定和K > 0, 存在一个使得如果Mn是一个带有积分曲率的完备黎曼流形, 则存在一个依赖于n,q,K 的常数Cs(n,q,K)使得

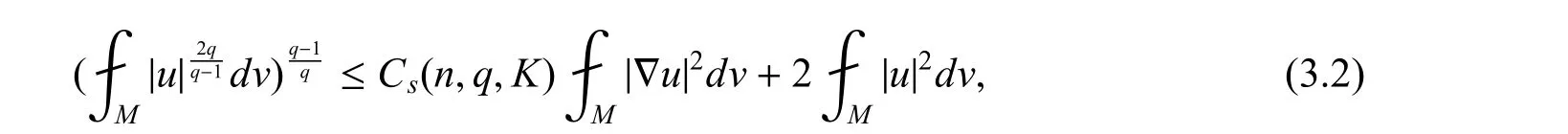
对任意的函数u ∈W1,2.

证由式(2.1),得到

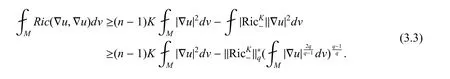
对函数|∇u|应用命题2 得到

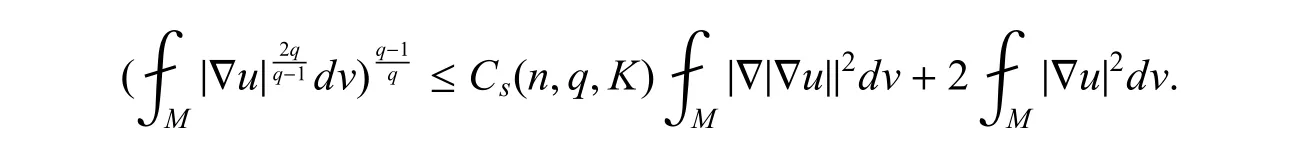
把上述所有加到式(3.3),就得到了这个结果.

进一步,可以得到以下引理.

引理2给定任意的以及K >0,都存在一个使得Mn是一个完备黎曼流形满足那么

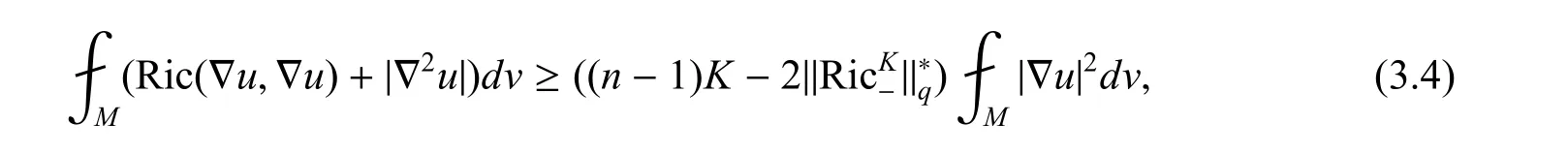
对所有的函数u ∈W1,2.

证由Kato 不等式,有. 引用引理1,得到

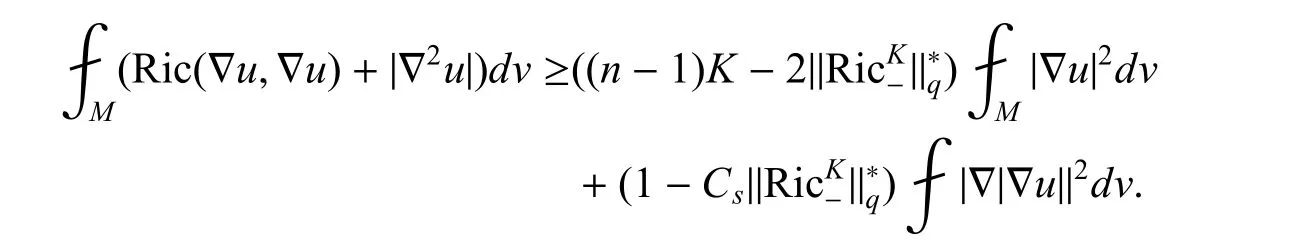
现在可以完成对定理1 的证明.

证由Bochner 公式由命题1,流形M 是闭的. 在流形M 上积分,得到了

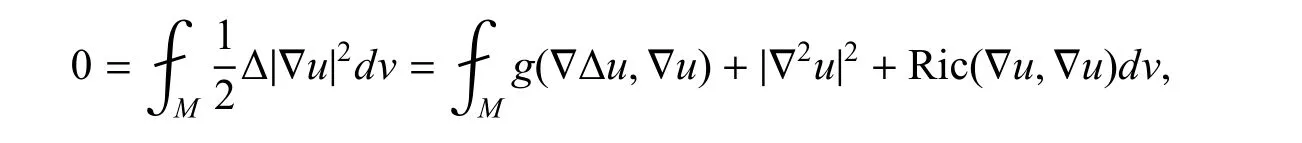
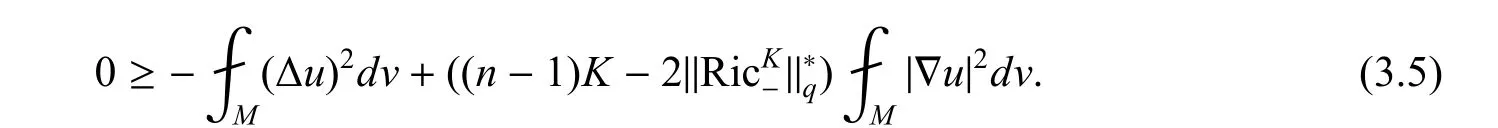
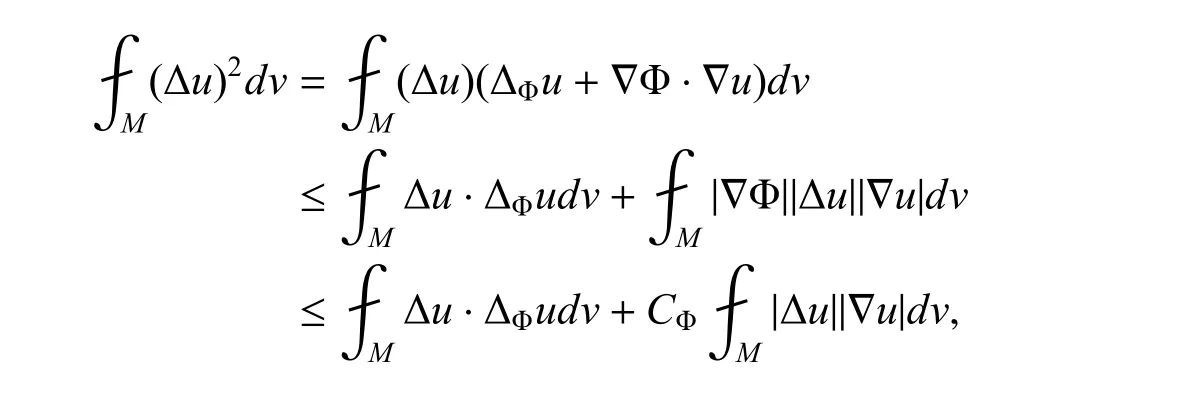
其中CΦ表示|∇Φ|在流形M 上的最大值,

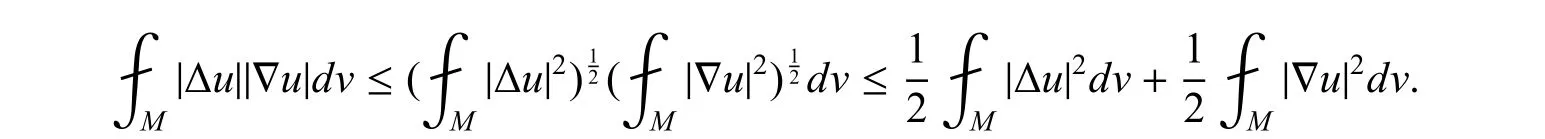
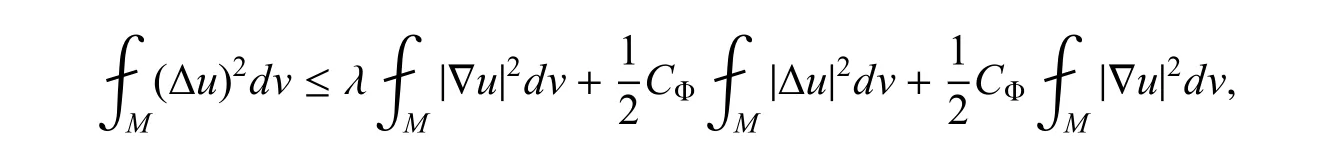
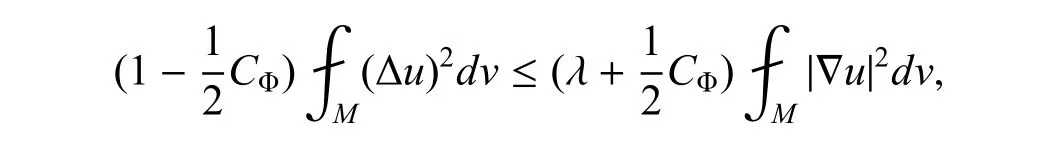
也就是

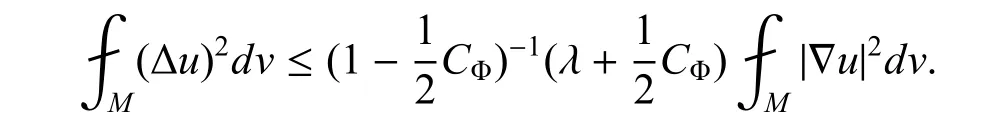
把所有式子带入到式(3.5),可以得到

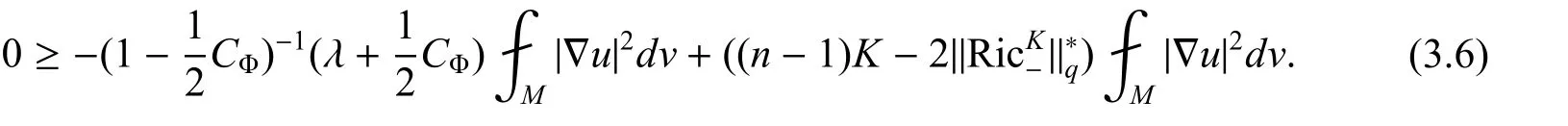
故

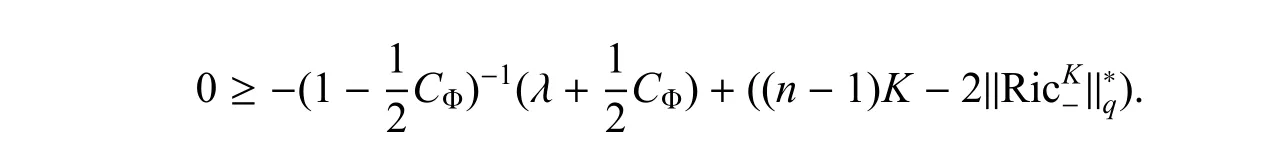
因此

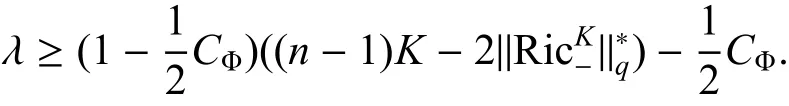
从而完成了这个证明.

接着给出定理2 的证明,这里先给出加权Laplace 算子的Reilly 公式.

命题3(见文献[12])

其中符号∂表示∂M 取内度量时的算子.

定理2 的证明注意到不管对Dirichlet 边界条件还是Neumann 边界条件,都有

在最后一步计算中,应用了对∂M 的假设. 因此有

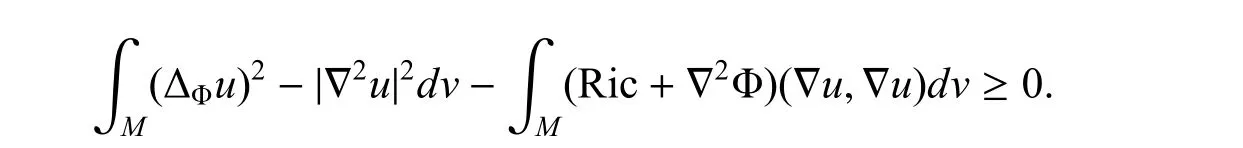
可以对等式两边同时取平均,

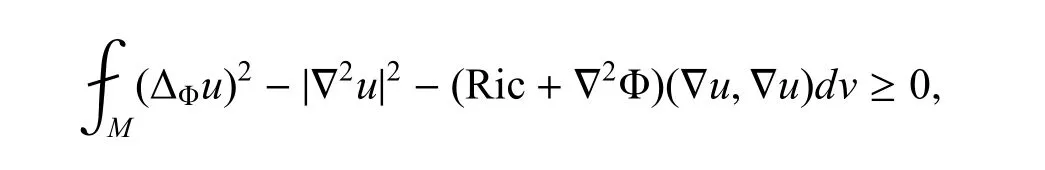
然后应用引理2,得到

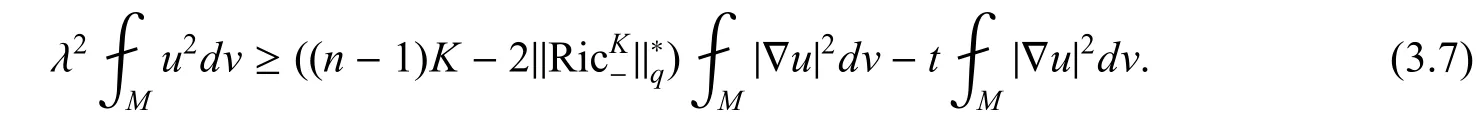
由假设,得到

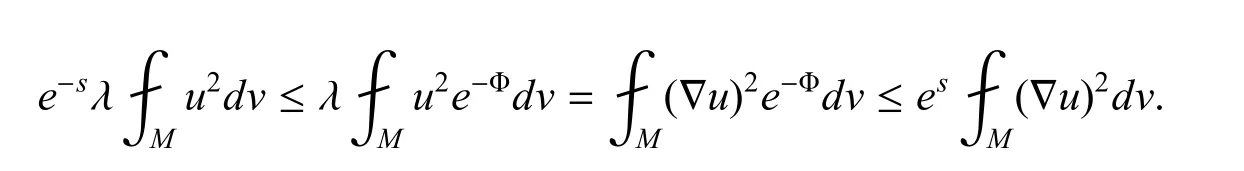
这也就是

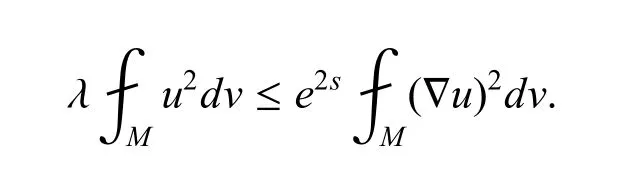
把上述式子加到式(3.7),得到了

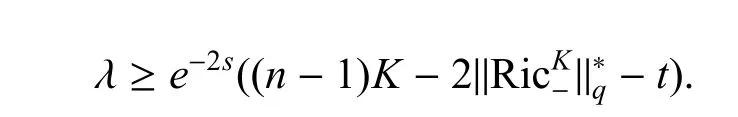
证毕.

定理3 的证明不妨假定+λu=0. 不失一般性,可以假设定义f 为M1上的函数满足在M 上,∆Φf =0.带有边值条件在∂M1上f =u. 由命题3 有

注意到

以及

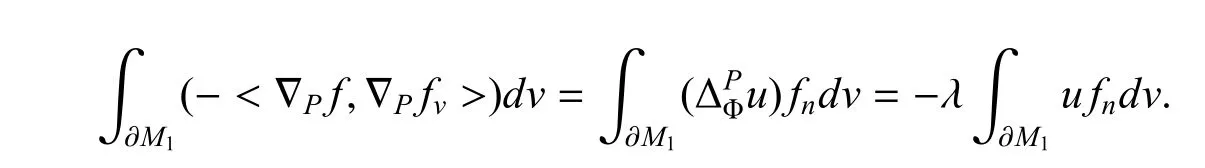
通过计算

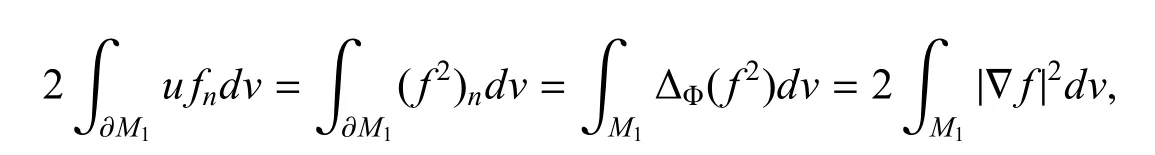
因此有

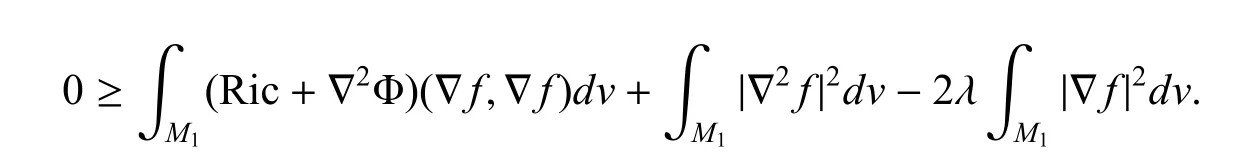
也即

应用引理2,得到

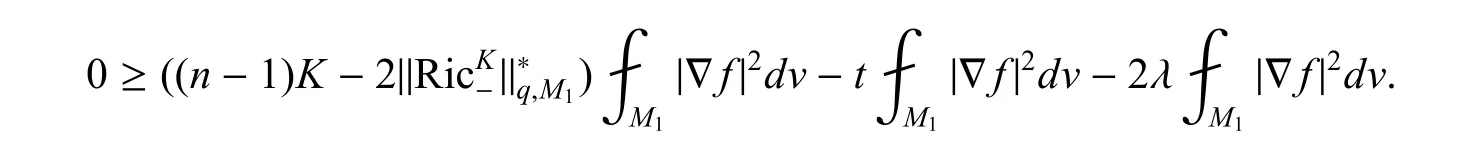
利用定理中的假设,

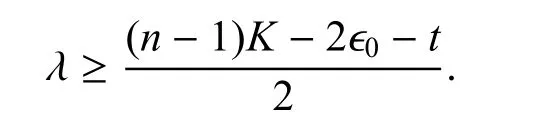
从而完成了证明.