变遗忘因子多新息随机梯度算法双馈电机参数辨识
2019-09-20
(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)
双馈感应发电机因其性能优良、结构可靠得到广泛应用,实际运行时,受温度、频率、饱和、杂散损耗等复杂因素的影响,电机参数容易发生改变,因此在许多应用场合,电机参数辨识具有重要的作用[1-2]。常见的待辨识电机参数包括定子电阻Rs、定子电感Ls、转子电阻Rr、转子电感Lr和定转子之间的互感Lm。
辨识分为离线辨识和在线辨识两种,其中在线辨识可以充分利用每次采集到的新数据,使辨识结果不断更新,从而克服慢时变和数据陈旧而引起的失效,在参数辨识中越来越得到重视[3-4],常见的递推最小二乘算法、随机梯度算法等都属于在线辨识。文献[5]在处理电机的瞬态过程中,采用脉冲电压法和脉冲电流法辨识电机参数,对数据实时处理的方法略显复杂;文献[6]采用基于遗忘因子最小二乘算法对永磁同步电机离散系统模型的转动惯量及负载转矩等进行辨识,虽然达到了辨识结果,但由于最小二乘算法需要计算协方差,导致计算量较大;文献[7]采用随机梯度算法辨识永磁同步电机参数,不用计算协方差阵,改进了最小二乘方法计算量的不足,但同时它的缺点是收敛速度比较慢,以上算法从各个方面验证了各自算法的有效性,但也存在各种不足,将多新息理论与传统随机梯度算法理论结合起来在一定程度上解决了这些问题,文献[8]将随机梯度算法与多新息思想结合,相对于传统随机梯度算法,增加了每次计算对数据的利用率,不仅减小了计算量,同时又大大提高了算法收敛速度。
本文将双馈电机dq坐标系下数学模型转化为标准辨识形式,采用定子磁链定向的矢量控制方法搭建双馈电机矢量控制系统并采集数据,利用变遗忘因子多新息随机梯度算法对双馈电机参数进行辨识,由仿真结果验证了算法的有效性。
1 双馈电机模型
1.1 dq坐标系下的双馈电机模型
在风力发电机系统中,双馈电机定子侧直接连接到电网,通常把定子侧电压和频率在运行中看作是恒定的,转子侧通常采用dq同步坐标系下解耦控制,用q轴分量irq控制有功分量,d轴分量inq控制控制双馈电机的无功功率。其基于定子磁链定向的空间矢量图如图1所示。

图1 定子磁链定向的DFIG空间矢量图
其中,αs、βs为静止坐标系下定子侧分量,αr、βr为静止坐标系下转子侧分量,θs为定子磁通角,θr为转子电角度,θslip为转差角,ψs为定子磁链。
假设定子采用发电机惯例,电流以流出为正,转子采用电动机惯例,电流以流入为正,经过Clark变换和Park变换,可以得到双馈电机在同步旋转dq轴坐标系下的数学模型[9-10]。
电压方程:
Usd=Dψsd-ω1ψsd-Rsisd
(1)
Usq=Dψsq+ω1ψsd-Rsisq
(2)
Urd=Dψrd-ω2ψrq-Rrird
(3)
Urq=Dψrq+ω2ψrd+Rrirq
(4)
式中,Usd、Usq分别为dq轴定子电压分量;Urd、Urq分别为dq轴转子电压分量;isd、isq分别为dq轴定子电流分量;ird、irq分别为dq轴转子电流分量;ψsd、ψsq分别为dq轴定子磁链分量;ψrd、ψrq分别为dq轴转子磁链分量;ω1为定子电流角频率;ω2为转子电流角频率;D为微分算子。
磁链方程为
ψsd=-Lsisd+Lmird
(5)
ψsq=-Lsisq+Lmirq
(6)
ψrd=Lrird-Lmisd
(7)
ψrq=Lrirq-Lmisq
(8)
式中,Lm为定转子互感;Ls为定子电感;Lr为转子电感。
电磁转矩方程为
Tem=1.5npLm(isqird-isdirq)
(9)
式中,Tem为电磁转矩;np为极对数。
运动方程为
(10)
式中,TL为负载转矩;J为转动惯量
式(1)~式(10)为双馈电机在同步旋转dq坐标系下的数学模型,通过坐标变换后,大大简化了交流电机的模型复杂度。
1.2 参数辨识模型
本文中双馈电机参数辨识在同步旋转dq坐标系下进行,所以需要将双馈电机在同步旋转dq坐标系下的数学模型变形为参数辨识的标准形式。旋转坐标系下,将定转子磁链方程带入到电压方程,则双馈电机在同步旋转dq坐标系下的数学电压方程可简化为
Usd=(-Disd+ω1isq)Ls+(Dird-ω1irq)Lm-isdRs
(11)
Usq=(-Disq-ω1isd)Ls+(Dirq+ω1ird)Lm-isqRs
(12)
Urd=(Dird-ω2irq)Lr+(-Disd+ω2isq)Lm-irdRr
(13)
Urq=(Dirq+ω2ird)Lr+(-Disq-ω2isd)Lm+irqRr
(14)
将式(11)~式(14)改写成矩阵形式:
(15)
(16)
对式(15)、式(16)中的微分算子D进行离散化处理:
(17)
(18)
(19)
(20)
将式(17)~式(20)代入式(15)、式(16),则得到在dq坐标系下双馈电机离散型参数辨识表达式为
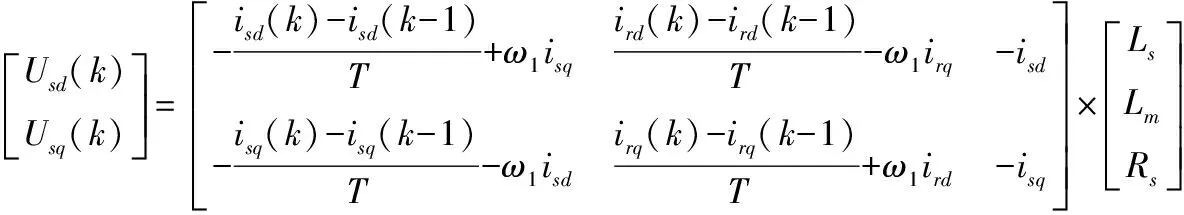
(21)
(22)
考虑定子侧的电流电压情况,双馈电机的自回归模型为
y(k)=φT(k)θ(k)
其中:
y(k)=[Usd(k)Usq(k)]T
(23)
φ(k)=
(24)
(25)
2 变遗忘因子多新息随机梯度算法
2.1 遗忘因子多新息随机梯度算法
对于线性回归模型:
y(t)=φT(t)θ+v(t)
(26)
式中,y(t)为输出向量;φ(t)为信息向量;θ为待辨识参数;v(t)∈R1为噪声向量。
令目标函数为J(θ)=‖y(t)-φT(t)θ‖2,其中X的范数定义为‖X‖2=tr[XXT],tr[X]表示X的迹。
根据梯度搜索原理极小化J(θ)得到式(27)~式(29)所示的随机梯度[11](Stochastic Gradient,SG)算法:
(27)
(28)
r(t)=r(t-1)+φ(t)2,r(0)=1
(29)

相比最小二乘算法,随机梯度算法不需要计算协方差阵从而减小了计算量,但是随机梯度算法的由于数据利用率低,导致收敛速度慢,为提高随机梯度算法参数估计的收敛速度,引入新息长度p,将原来的单新息量e(t)扩展到数据长度为p的多新息向量,提高了每次计算对数据的利用率,得:
(30)
Φ(p,t)=[φ(t)φ(t-1) …φ(t-p+1)]∈R1×p
(31)
Y(p,t)=[y(t)y(t-1) …y(t-p+1)]∈R1×p
(32)
其中y(t-i),φ(t-i):i=1,2,…,p-1表示过去时刻的值。
式(28)可以表示为
(33)
根据随机梯度算法得到多新息随机梯度算法:
(34)
(35)
r(t)=r(t-1)+Φ(t)2,r(0)=1
(36)
相比传统的随机梯度算法和最小二乘算法,多新息随机梯度算法将新息的数据长度扩展为p,使数据得到比较充分的利用,同时避免最小二乘算法中因为要计算协方差而造成的计算量较大的情况[12],是两种算法的折中。
2.2 变遗忘因子
新息长度的引入可以改善参数收敛精度,但这种改进是有极限的,特别在待辨识参数数目多时,可在多新息随机梯度辨识方法中引入遗忘因子得到多新息遗忘梯度算法。
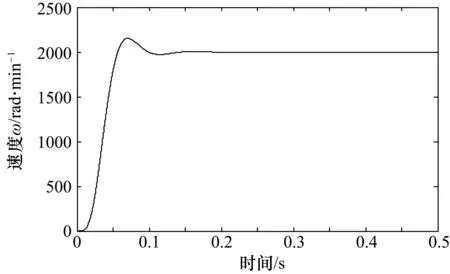
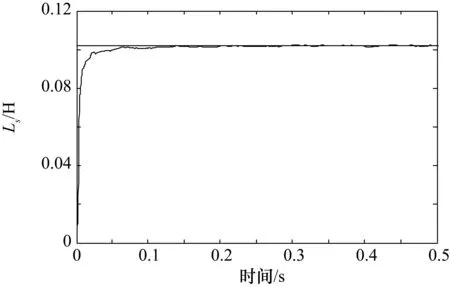
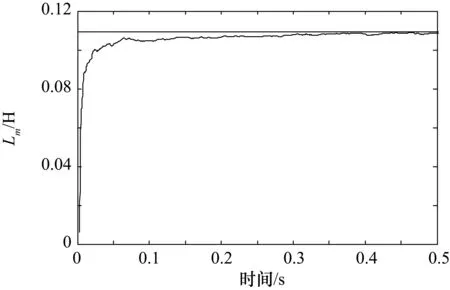
用FF表示遗忘因子,其中0 r(t)=FF·r(t-1)+φ(t)2 (37) 多新息遗忘梯度算法相比于传统的随机梯度算法有一定的改进,但固定的遗忘因子有时并不能满足需要,在非平稳的情况下,通常希望FF足够小,使算法能够很快跟踪上非平稳信号的局部趋势;在稳态情况下,希望FF能够逐渐变大到一个合适的值,以减小参数的估计误差[14];故提出可变遗忘因子,通过检测系统的误差更新遗忘因子的大小。 通过检测系统的真实输出,并计算与估计输出值的差值的范数得到t时刻的输出误差δ(t)。定义t时刻遗忘因子的更新公式为 (38) 式中,(FF1,FF2)是FF的变化范围,r(t)=FF(t)·r(t-1)+φ(t)2为容许的最大误差,并规定当δ(t)>t时,取δ(t)=δ;在r(t)=FF(t)·r(t-1)+φ(t)2时,取δ(t)=0.2δ,其中δ为系统参数与真实参数误差的范数,即系统参数的辨识误差[15]。代入得到式(39): r(t)=FF(t)·r(t-1)+φ(t)2 (39) 将该算法与电机模型结合起来,采集电机运行中电流、电压等相关数据,构建算法中信息向量和输出向量,根据变遗忘因子多新息理论迭代刷新估计参数值,从而得到电机参数的辨识结果,其流程图如图2所示。 图2 电机参数辨识流程图 矢量控制是将电机的电压或电流矢量进行变换,将其解耦为正交的励磁电流和转矩电流并分别进行控制。双馈电机由于其非线性、强耦合性,控制较为复杂,因此将矢量控制技术引入到双馈调速系统中,并对坐标轴间的交叉耦合进行有效的补偿,在Simulink中搭建永磁同步电机矢量控制模型[16-18],如图3所示。 图3 双馈电机矢量控制系统 由于DFIG定子侧绕组直接连在无穷大电网上,通常将定子的电压幅值、频率近似看作恒定的。采用定子磁链定向时,假定定子磁链矢量与d轴方向一致,可以得到: (40) 忽略定子电阻,可以得到: (41) (42) 电机模型参数为:额定功率Pn=2.8 kW,额定电压Un=380 V,定子电感Ls=0.102 H,定子电阻Rs=1.31 Ω,定转子互感Lm=0.109 H,极对数np=2,额定转速n=2000 r/min。图4为转速跟踪仿真,从图中可以看出,该矢量控制模型有很好的控制效果,超调约为6%,且抗干扰能力较好。 图4 转速跟踪(ω =2000 rad/min) 参数辨识步骤如下。 ① 采集电机中电流isdq、irdq和电压Usdq、Urdq等数据,并进行滤波处理。 ② 根据式(23)、式(24)的值构造y(k)、φ(k)。 ③ 根据式(31)、式(32)构造Φ(p,t)、Y(p,t)。 ④ 根据式(30)计算E(p,t),根据式(39)计算r(t)。 ⑥ 在线采集新数据,t=t+1,返回步骤②。 辨识结果如图5~图7所示。 图5 定子电感Ls辨识结果 图6 互感Lm辨识结果 图7 定子电阻Rs辨识结果 图5为变遗忘因子多新息随机梯度算法对双馈电机定子电感Ls的辨识结果,从图中可以看出,在0.1 s内算法快速收敛,后虽略有波动,但误差极小,精度理想。 图6为辨识算法对双馈电机定转子互感Lm的辨识结果,从图中可以看出,约在0.1 s系统达到收敛效果,误差控制在0.2%内,随后缓慢收敛于实际值。 图7为变遗忘因子多新息随机梯度算法对双馈电机电阻Rs辨识的结果。可以看出,参数辨识结果在0.15 s接近于实际值,误差控制在0.01以内,算法辨识精度理想。 本文采用定子磁链定向的矢量控制方法,在Simulink中搭建电机控制系统模型采集电压电流信号,根据电机数学模型推导参数辨识表达式,并结合梯度辨识思想,提出了一种基于变遗忘因子多新息随机梯度算法的双馈电机参数辨识方法。相比最小二乘辨识方法,避免计算协方差矩阵,从而大大减少了计算工作量;而相对于随机梯度辨识方法,扩展新息长度并加入时变遗忘因子,充分利用过去时刻数据,提高了系统辨识的速度,由仿真结果分析,变遗忘因子多新息随机梯度算法通过调节遗忘因子的大小,能够较有效跟踪参数的变化。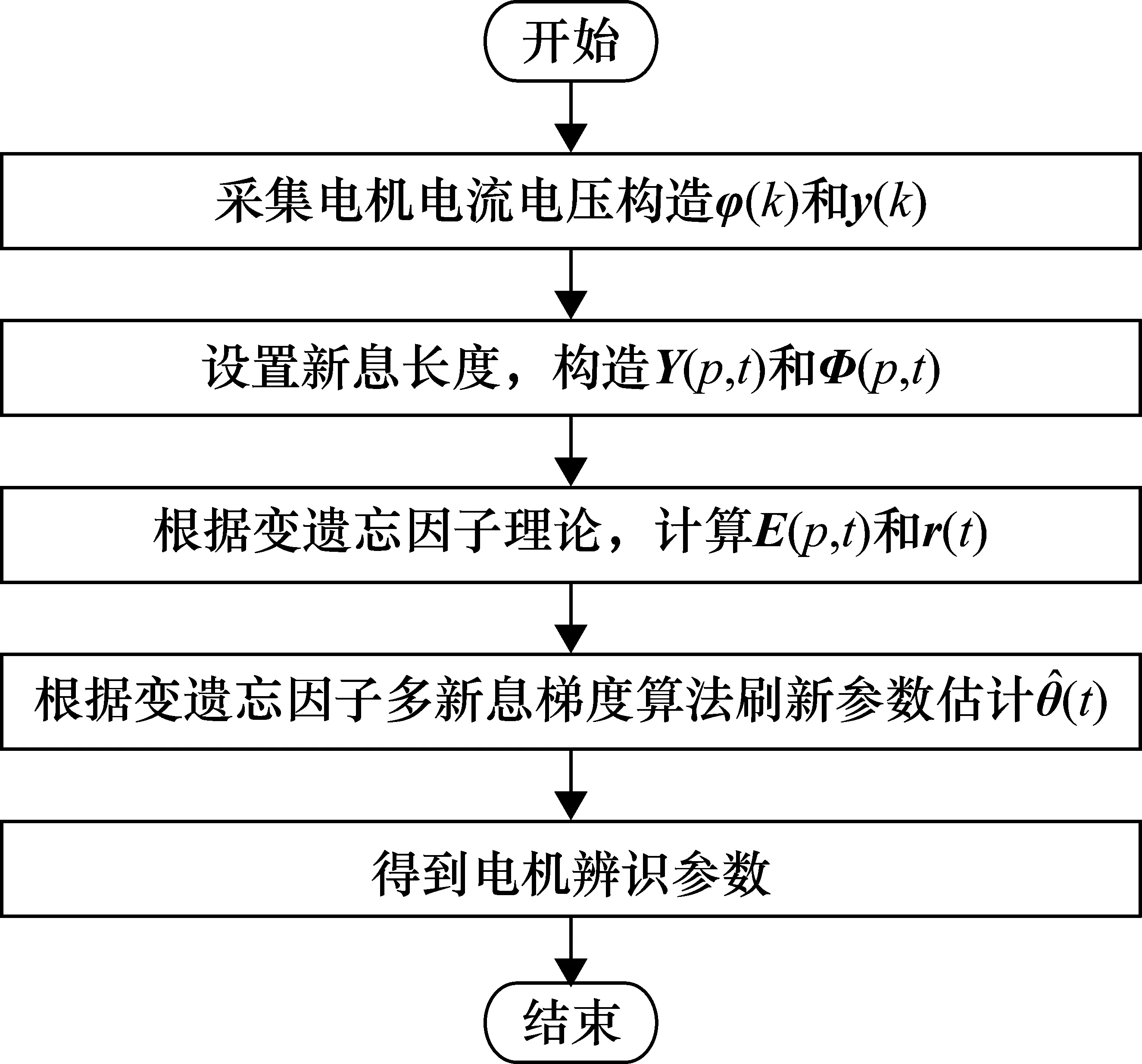
3 仿真实验
3.1 控制系统仿真

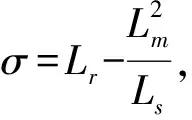
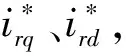
3.2 电机参数辨识

4 结束语
