含有时滞的怠速控制与输出扭矩估计器设计

李学军1， 穆宏慧， 于聪梅

(1.东北师范大学 人文学院理工学院,吉林 长春 130022;2.长春科技学院 信息工程学院，吉林 长春 130600)

发动机怠速控制系统的控制目标明确，但存在固有的非线性和时滞现象。时滞包括状态滞后和信息传输过程中的间隔滞后。时滞现象不仅影响系统性能，且能恶化系统稳定性[1-3]。时滞对怠速控制系统性能的影响也会改变车辆的运行性能，即发动机输出扭矩受转速的影响较大。发动机扭矩的输出经离合器、变速箱、传动轴、差速器和半轴构成的传动系传递到车轮，决定了车辆的动力特性[4]，尤其在怠速工况向启动工况转换时，即离合器接合过程中,接合控制的是否平顺与发动机输出扭矩直接相关。因此，本文针对发动机怠速控制系统存在的不确定扰动量及时滞引起的控制性能下降的问题，基于Lyapunov函数，考虑时滞对系统的影响，设计了含有时滞信息的H∞反馈控制器，使闭环控制系统对外界扰动量具有鲁棒性的同时改进时滞带来的性能下降，即在保证执行控制量的节气门切换尽量少的同时使怠速时的转速尽量稳定。在怠速稳定的基础上，设计H∞滤波器在线估计发动机怠速时输出扭矩，为离合器控制提供力矩信息。构造含有时滞的Lyapunov函数，给出时滞滤波误差系统满足渐近稳定，并且使误差系统的误差输出与扰动输入传函的H∞范数小于正的实常数γ。在设计滤波器时，考虑了怠速系统自身具有的时滞因素，并利用非时滞系统的无偏滤波思想，降低滤波器的维数，使得滤波计算量也随之降低。

1 发动机怠速工况时滞系统建模

本文的研究对象为缸内直喷汽油机，采用典型的面向控制分析的发动机模型——平均值模型。这种模型基于发动机的一个或几个循环来预测平均的外部变量和内部变量的值。参考文献[5]与文献[6]，发动机模型分为节气门、进气歧管、燃烧室和曲轴4个子系统，其组成如图1所示。

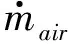
(1)

其中，

(2)

(3)

式中，Cd为流量系数；dth为圆形节气门直径；Aleak为节气门漏极面积；α为节气门开启角度；P0为大气压；T0为空气温度(常值)；R空气质量常数；ρ0为大气密度；Vcyl为进气歧管容积；η为发动机容积效(常值)；n为发动机转速。根据发动机动力学规律，发动机转速动态模型为

(4)

式中，Tind为指示扭矩；Tfric、Tpump和Tload分别为经过折算作用在发动机曲轴上的摩擦扭矩、泵气扭矩和负载扭矩；J为发动机转动惯量。本文研究的怠速系统鲁棒控制指当外界扭矩Tload发生变化时，怠速工况下的转速n的变化对Tload的扰动具有鲁棒特性，同时估计出当外界扭矩Tload变化时曲轴输出力矩的大小，为车辆启动时离合器的顺畅结合提供力矩信息。由发动机工作原理可知，稳态下空气流经节气门到燃烧室，燃油喷射、点火到力矩输出这两个环节都存在时间延迟。由文献[6]、文献[7]可知，在稳定的发动机转速条件下，滞后时间为一常数，与发动机转速成反比，取其上界值。则考虑滞后的发动机扭矩输出与进气量的动态描述为

(5)

根据发动机输出力矩与输出转速间的关系：

(6)

(7)

式中，Te为发动机输出扭矩；Tl为外部干扰扭矩；f1(N)为指示效率函数；λ为空气燃油质量比；H1为生热系数。基于Simulink工具箱搭建式(1)～式(7)描述的含有时滞环节的非线性系统，系统结构参数参考文献[7]与文献[8]。选取电子节气门角度为α0=8.75°；负载扭矩为T0=10 N·m时，验证发动机非线性模型性能，验证曲线如图2所示。

从仿真结果可以看出，发动机震荡后稳定的转速、进气歧管压力和泵吸扭矩基本稳定在n0=800 r/min，P0=5.42×104Pa，Tpump=4.67 N·m上。

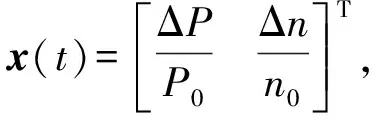
(8)

输出方程为

y(t)=Cx(t)+Dw(t)

(9)

待估计状态方程为

z(t)=Czx(t)+Dzw(t)

(10)

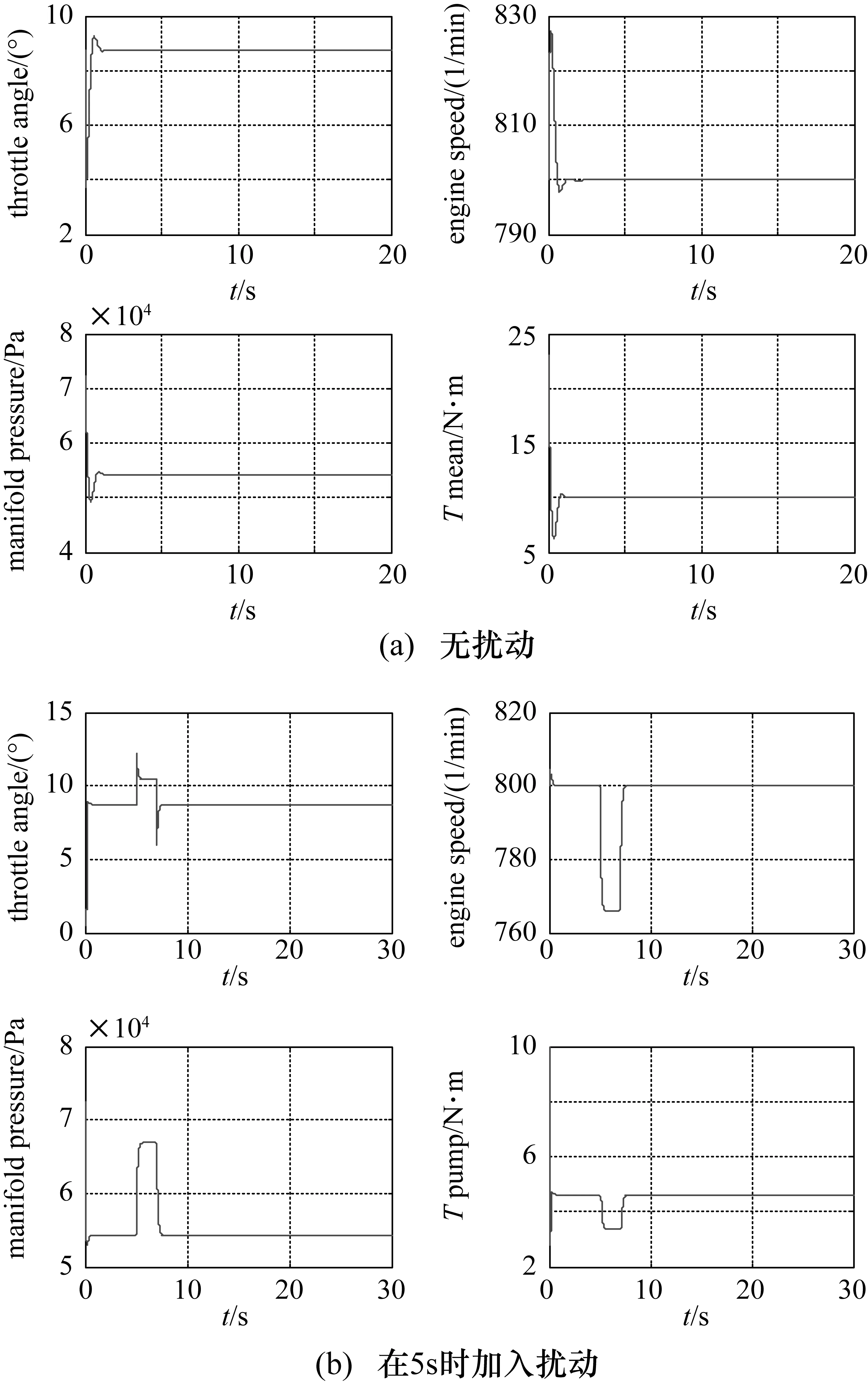
图2 模型在输入恒定时的响应曲线

在理想情况下，忽略发动机的参数蠕变和未建模动态，得到发动机怠速时的线性系统的结构参数为

2 含有时滞的鲁棒滤波器设计

发动机输出力矩受转速影响较大。怠速工况理想状态希望在干扰扭矩如空调的开关、转向助力的使用等影响下转速恒定。为精确估计怠速工况下发动机输出力矩，首先设计鲁棒控制器保证怠速时转速恒定，再设计含有时滞环节的鲁棒滤波器在线估计发动机怠速时的输出力矩，为后续车辆启动时离合器平顺接合提供精确的输入扭矩。基于Lyapunov理论，针对含有x(t-τ)状态时滞的怠速控制系统，设计时滞依赖的H∞状态反馈控制律u(t)=Kx(t-h(t))，使怠速系统:① 闭环系统是渐近稳定；② 在零初始条件下，对任意能量有界扰动w(t)∈L2[0,∞)满足‖z(t)‖2<γ‖w(t)‖2，其中γ为大于零的实常数。

定理1 对任意给定常值γ1>0，hm>0,hM≥hm以及αi(i=0,1,2,3),若存在矩阵P>0,R0>0,R1>0,R2>0,S>0以及任意矩阵Y,Q1,Q2,Q3,Q4,Q5,Q6,使得

(11)

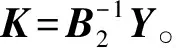
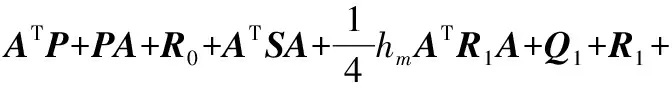
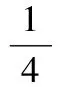
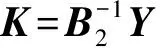
(12)

式中，Af,Bf,Cf,Df均为待定滤波器的参数矩阵。滤波器的设计问题转化为由式(8)～式(10)和式(12)构成的滤波误差系统满足渐近稳定和H∞性能指标要求问题。定义误差系统的状态和输出分别为

则

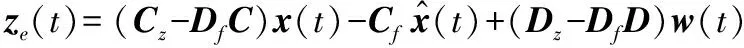
(13)

根据无偏滤波器的设计思想[9]

(14)

则式(13)演变为

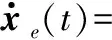
=Aexe(t)+Ade(t-τ)+Bew(t)

ze(t)=(Cz-DfC)xe(t)+(Dz-DfD)w(t)

=Cexe(t)+Dew(t)

(15)

当扰动量w(t)是具有单位方差的零均值白噪声过程，且x(0)=0时，基于无偏条件，估计误差的均值都为零，这样得到的滤波器(12)即为无偏滤波器。由式(15)可知，Ae=Af，误差系统的稳定性由滤波器的稳定决定，与待估计系统的稳定与否无关。

根据有界实引理，在滤波误差系统渐近稳定的前提下，推导出衡量时滞无偏滤波误差系统性能好坏的准则，即由时滞系统和滤波器构成的滤波误差系统对外部的扰动抑制能力为γ(‖Tzew(t)‖∞<γ)的线性无偏滤波器存在的充分条件，求出无偏滤波器的参数。

定理2 对给定的常数γ>0，误差系统(13)稳定且存在一个H∞滤波器(12)，当且仅当存在对称正定矩阵P,S和常阵Y,Df，使得

(16)

成立。其中，Δ=ATP+PA-CTYT-YC+S。设计的滤波器参数为

(17)

证明：H∞性能指标定义为

选取正定的Lyapunov函数为

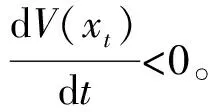
V(x(t))|t=∞-V(x(t))|t=0

(18)

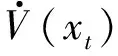
wT(t)(Dz-DfC)T(Dz-DfC)w(t)+

[(A-BfC)xe(t)+(A1+B2K)xe(t-τ)]T

整理，得

对任意xe(t),w(t),xe(t-τ)，不等式J<0等价于

Δ1=(A-BfC)TP+P(A-BfC)+S+(Cz-DfC)T(Cz-DfC)
Δ2=P(B1-BfD)+(Cz-DfC)T(Dz-DfD)
Δ3=(Dz-DfD)T(Dz-DfD)-γ2I

应用Schur补公式，整理得到式(16)。证毕。

控制律与估计器设计算法：

① 考虑式(8)、式(9)构成的系统，给定正实数γ1>0。

② 求解线性矩阵不等式(11)存在对称正定矩阵P,R0,R1,R2,S和任意矩阵Y,Qi(i=1，2，…，6)的可行性解；若可行性解不存在，转到第③步。若解存在，转第④步。

③ 增加γ1，转第②步。

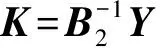
⑥ 考虑式(8)、式(10)和式(13)构成的滤波误差系统，给定一个实常数γ>0。

⑦ 求解线性矩阵不等式(16)有关P>0和S>0关于矩阵变量Y、Df的可行性问题，若可行解存在，转到第⑧步，否则转第⑨步。

⑧ 由式(17)计算出γ-次优滤波器的参数(Af,Bf,Cf,Df)。

⑨ 增加γ，转第⑦步。

3 设计仿真验证

根据第2节建立的式(9)和式(10)得到电子节气门的动态数学模型：

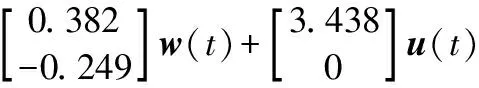
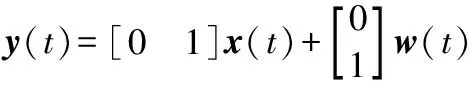
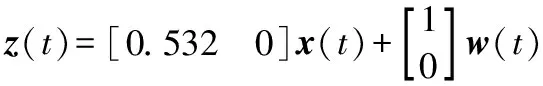
给定γ1>0.028，由控制律与估计器设计算法步骤①～步骤④得到状态反馈增益K1=[-8.9630 -54.2038]。考虑系统固有时滞，得到怠速控制控制系统的响应曲线如图3(a)所示。考虑控制律所产生的时滞u(t)=Kx(t-h(t))得到的响应曲线如图3(b)所示。可以看出，图3(a)中的电子节气门在初始响应过程变化幅度较大，处于频繁切换状态，约1.5 s后稳定下来；图3(b)电子节气门的变化幅度比图3(a)略小，没有产生频繁的切换，其他的指标基本区别不大。由此可见本文设计的控制律效果稳定，节气门切换不频繁，输出曲线比较光滑。

为方便对比分析，图4给出常规的PID控制算法设计的控制系统的状态变量和转速变化曲线。对比发现采用PID控制器控制怠速的转速，输出转速变化小，跟踪好，但电子节气门的切换频繁，且幅度大，实际电子节气门处于剧烈震荡状态下，输出扭矩有幅度高达30 N·m的剧烈变化，平稳性差，进气歧管压力变化也非常大，导致扭矩变化也很敏感。通过图3(b)和图4比较可见，H∞控制器的鲁棒性较好，综合控制效果稳定，节气门切换不频繁且曲线变化比较光滑。

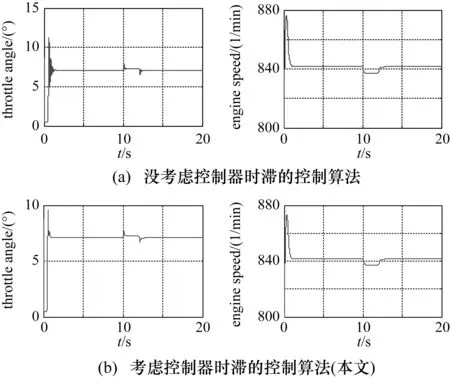
图3 怠速控制系统的状态变量和转速变化曲线

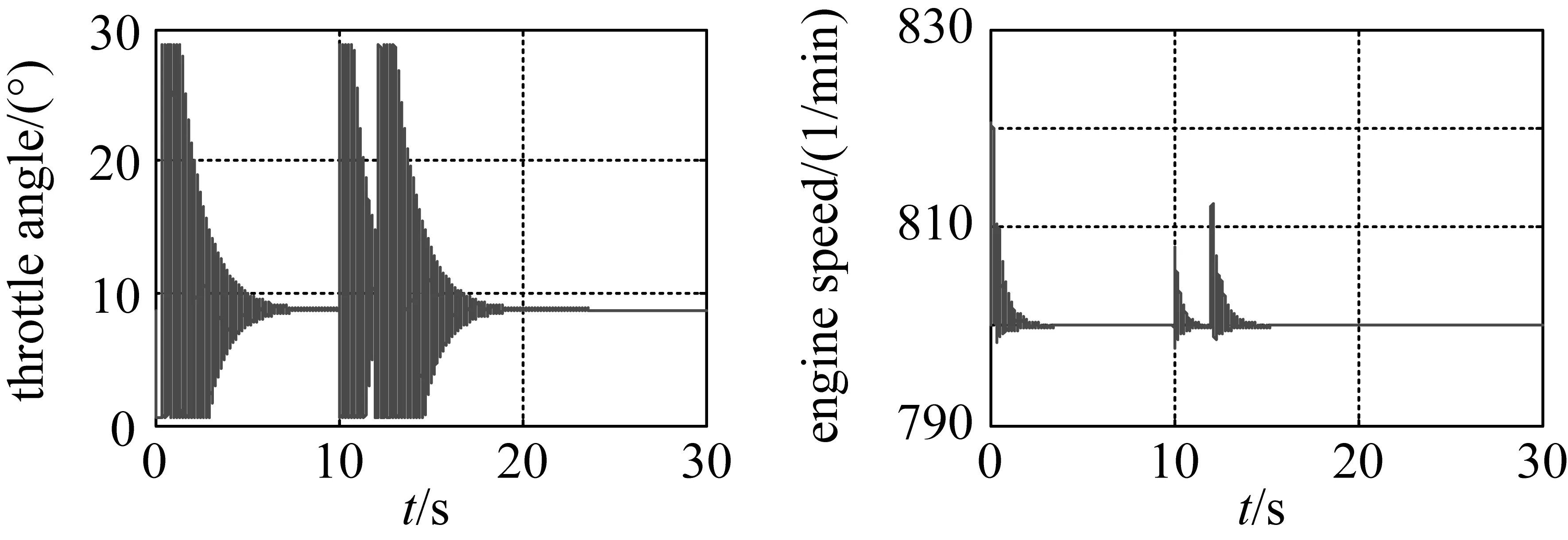
图4 PID控制算法的状态变量和转速变化曲线

根据算法步骤⑤～步骤⑨，对怠速状态输出扭矩估计进行仿真验证。设t=(20～25) s时，加入幅值为10 N·m的阶跃扰动信号。取γ=0.847，采用本文算法设计的估计系统状态变量的变化曲线如图5所示。得到的滤波器参数分别为

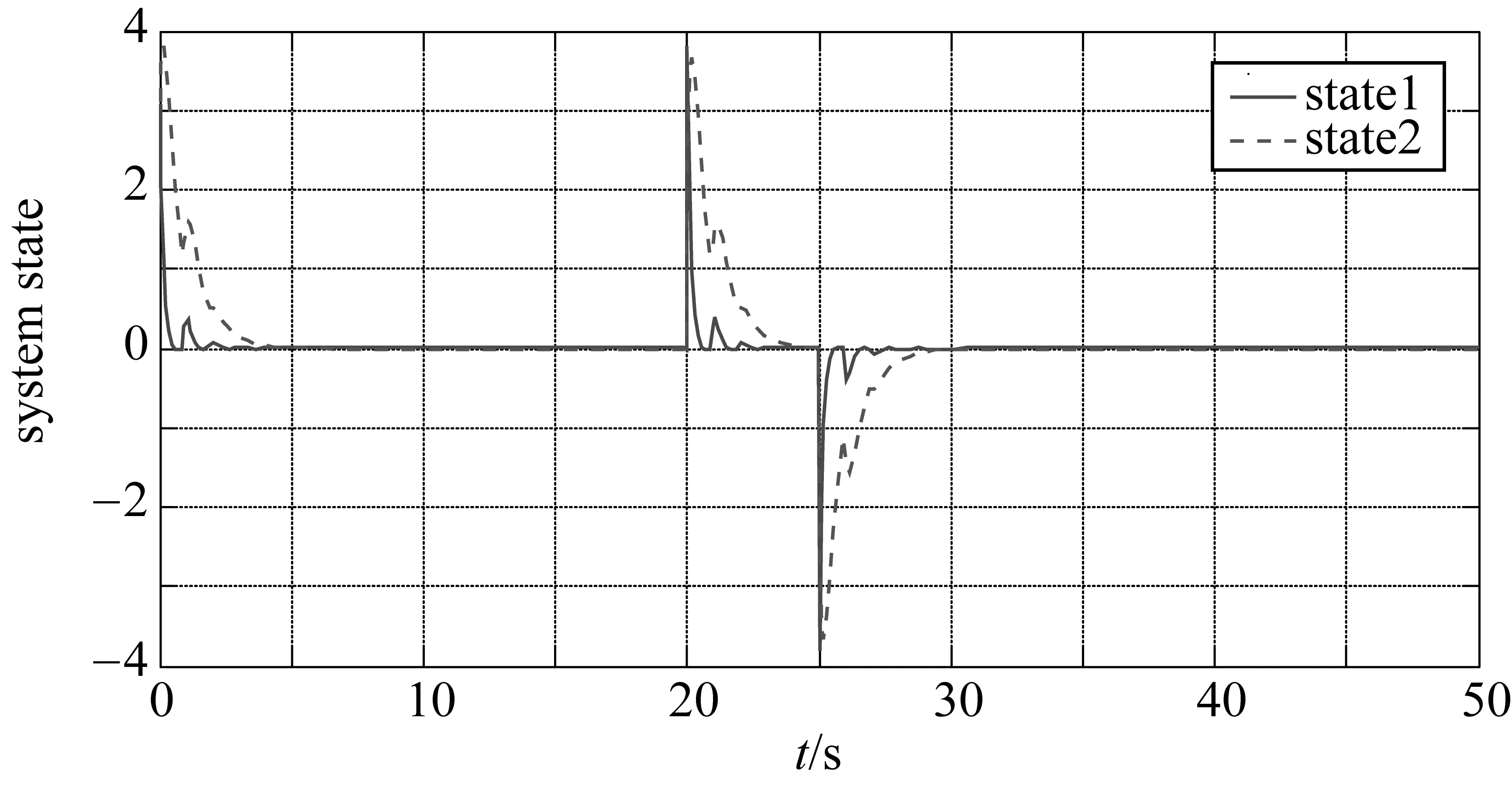
图5 怠速状态扭矩输出估计系统状态曲线

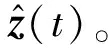
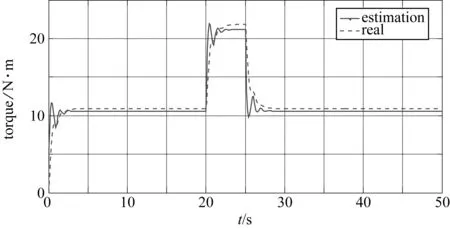
图6 发动机输出扭矩曲线

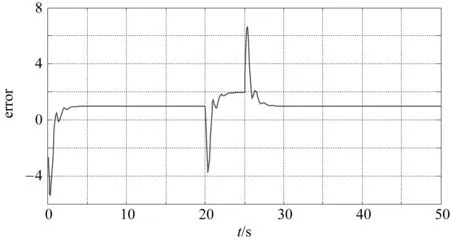
图7 估计误差曲线

4 结束语

根据发动机怠速工况下的工作原理，针对GDI发动机基于机理和仿真验证法建立含有状态时滞的数学模型。设计含有时滞的H∞状态反馈控制规律和含有时滞的H∞鲁棒估计器估计发动机输出扭矩，给出系统满足性能指标和控制器、估计器存在的条件。基于Matlab中的Simulink工具箱建立了发动机仿真模型和控制器与估计器。并对文中提到的时滞控制器和估计器与发动机怠速工况下的时滞系统构成的控制系统进行仿真验证及分析。仿真结果表明设计控制规律和滤波器时考虑时滞信息能保证执行控制量的节气门切换尽量少，同时使怠速时的转速稳定，能有效估计发动机怠速时输出扭矩，为离合器控制提供力矩信息。