重复使用运载器低温贮箱结构疲劳寿命与可靠性分析
2019-09-20马云龙
马云龙,王 朔,贺 丹
(1.北京宇航系统工程研究所 结构室,北京 100076;2.沈阳航空航天大学 航空宇航学院,沈阳 110136)
随着航天工业的迅速发展,未来空间运载器将以低成本、高运载能力两大特点为发展目标,低成本运载器(ELV)、单级入轨航天器(SSTO)以及可重复使用运载器(RLV)等都将成为重点研究项目[1]。2011年随着美国航天飞机全部退役,可靠的新型可重复使用运载器(RLV)的研制受到国际航天领域的关注。要实现单级入轨和可重复使用,必须采用超轻型结构和使用高性能发动机。在轻质结构中,可重复使用的低温贮箱一直被视为RLV研制中的最大的难题[2]。低温贮箱是可重复使用运载器(RLV)推进系统的重要组成部分,其功能是在地面和飞行使用环境中贮存低沸点的液态火箭推进剂,倘若其结构发生失效易导致灾难性后果。2003年,哥伦比亚号航天飞机事故导致7名美国航天员全部遇难。NASA调查发现,引起事故的主要原因之一就是航天飞机外部燃料贮箱热防护层的结构失效,这引起了航空航天领域相关机构和研究人员的高度重视[3]。因此,根据RLV的重复使用特性,保证低温贮箱结构的可靠性对保持RLV安全性和完整性具有重要的意义[4]。
一般来说,运载器结构的疲劳破坏是其破坏的主要形式,也是航空航天领域最为关注的失效形式之一[3,5]。对承受交变载荷作用的运载器低温贮箱结构,进行疲劳强度及可靠性的分析与计算,估算结构使用寿命,预测结构在使用中发生失效的概率,在一定程度上预防贮箱结构在运行条件下的失效。本文针对RLV贮箱结构的疲劳可靠性问题,以分析贮箱结构失效的物理原因为出发点,研究贮箱结构在相应的运行时间和状态下抵抗失效的能力[6-9]。贮箱结构可靠度作为衡量其可靠性的重要指标,可通过定量的分析RLV低温贮箱结构在特定环境下的受载情况和强度退化关系计算得到。因此,在获取RLV贮箱结构的实测应力谱的情况下,可靠性计算的基本工作就是贮箱结构的失效概率。
1 结构疲劳可靠性分析方法
1.1 材料疲劳性能S-N曲线
材料的疲劳性能用应力S与到破坏时的寿命N之间的关系描述,即材料承受疲劳载荷和其在该载荷下发生疲劳破坏所经历循环次数的关系曲线,可以通过疲劳实验来确定[10]。大量实验表明,正态分布(Normal Distribution)或对数正态分布(Logarithmic Normal Distribution)能较好模拟疲劳寿命分布规律,通过成组法测定不同应力下中短寿命区的疲劳寿命数据,通过升降法测定材料疲劳极限寿命数据。利用测定的数据点拟合疲劳寿命曲线的三参数方程[11]
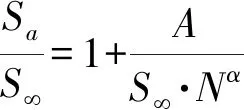
(1)
式(1)中:ρa为交变载荷(MPa),ρ∞为结构的疲劳极限(MPa),N为疲劳寿命(cycle),A,α为疲劳曲线形状参数。通过母体推断,可以得到不同存活率下的寿命值,计算出不同存活率下的S-N曲线,结合基于疲劳损伤的可靠性分析模型,可以计算不同疲劳寿命下结构的可靠度。
1.2 疲劳累积损伤理论
工程结构的疲劳破坏是材料内部疲劳损伤的逐渐累积过程。根据Miner线性疲劳累积损伤理论,当构件在交变载荷作用下其损伤度之和等于1时,构件发生疲劳破坏[12]。构件在应力水平Si作用下,经受ni次循环的损伤为Di=ni/Ni,若在k个应力水平Si作用下,各经受ni次循环,则可定义其总损伤为
(2)
破坏准则为
D=∑ni/Ni=1
(3)
式中,ni是在Si作用下的循环次数,由载荷谱给出;Ni是Si作用下循环到破坏的寿命,由S-N曲线确定。
2 贮箱疲劳寿命可靠性分析模型
贮箱由两端半球形封头和中间圆柱形筒体组成,中间有一隔板将贮箱分成上、下两部分,通过表面张力作用实现微重力环境下推进剂的加注与排放。贮箱壳体材料采用铝合金LD10,材料的主要性能参数见表1,推进剂为液氧,密度为1 140 kg/m3。在进行有限元建模时,由于贮箱壳体内径远远大于壁厚,因此可视为薄壁结构,对于薄壁容器,一般采用壳单元分析更为准确,该模型采用壳单元模拟结构。
2.1 飞行任务剖面和疲劳载荷谱
可重复使用运载器执行一次飞行任务要经历起飞、惯性力最大、上升段Qa最大、上升段跨音速、轴向过载最大、法向过载最大、返回段Qa最大、返回段跨音速、降落和滑行共10个典型飞行状态。根据贮箱有限元应力分析,在各个典型的飞行过程中,贮箱圆弧底面与直筒连接部位应力均为最大,为疲劳危险部位,最容易出现疲劳裂纹,如图1所示。

表1 LD10材料参数

图1 几个典型飞行过程中的贮箱的受力图
结构飞行状态损伤是指贮箱在特定的飞行状态下,经历的载荷-时间历程对结构所造成的损伤。疲劳损伤评估过程中,依据可重复使用运载器的飞行谱及各个飞行状态所占的比例,编制飞行载荷谱。根据贮箱结构的典型工况,结合实测载荷谱,利用雨流计数法,确定飞行谱中各种飞行状态对应的贮箱周期性载荷的幅值特征和频数,形成了贮箱结构地-空地循环应力谱,如表2所示。

表2 地-空地循环应力谱
2.2 无限寿命设计的应力-强度干涉模型
按照疲劳可靠性的观点,“无限寿命设计”是指结构以一定可靠度和置信度在无限长的使用期间不出现疲劳裂纹[13]。利用结构疲劳寿命的概率分布与相应的疲劳强度概率分布之间存在的确定的关系,采用安全寿命设计来保证结构在使用中的安全。假设贮箱疲劳应力和疲劳极限为两个相互独立的正态变量X1和X2,其正态概率密度函数分别为[14]
(4)
式(4)中,σ1和σ2分别表示疲劳应力和疲劳极限的母体标准差,并假定疲劳应力母体平均值μ1小于疲劳极限母体平均值μ2,正态概率密度曲线如图2所示。
结构的可靠度R等于X2大于X1的概率
R=P(X2>X1)=P(X2-X1>0)
(5)

图2 疲劳应力和疲劳极限干涉模型
令ξ=X2-X1,ξ仍为正态变量,其母体的均值和标准差分别为
(6)
ξ的概率密度函数为
(7)
已知ξ的概率密度函数,即可通过标准正态分布函数Φ(β)求出贮箱结构的可靠度R。其中,β为可靠度指标
(8)
在实际应用中,母体参数μ1、μ2、σ1和σ2均以具有一定置信度γ的估计量代替。当满足式(5)时,可保证构件以可靠度p和置信度γ在无限长的使用期间内不出现疲劳裂纹。
为了进行无限寿命可靠性设计,首先必须解决构建疲劳极限的概率分布问题。假设应力和强度服从正态分布,可将正态分布函数转换为线性方程
Z=B·X+A
(9)
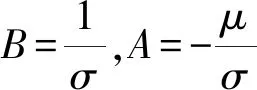
对于一组已知的安升序排列的随机变量数据xi(i=1,2,…,n),由于数据有限,第i个数据的试验概率值Fe(xi)采用下式计算
Fe(xi)=i/(N+1)
(10)
对本文所讨论的任一分布,可以用实验值代替理论值,并获得一(Xi,Yi)组数据。用最小二乘法拟合得到其斜率B和截距A的点估计值
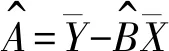
(11)
(12)
式中:
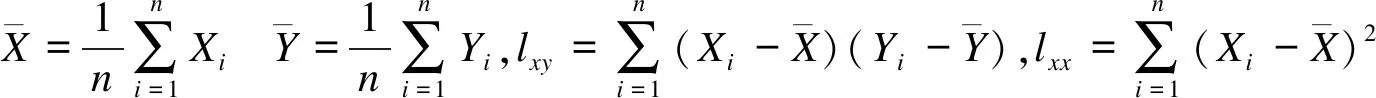
(13)
表3为10个典型飞行状态下贮箱的应力水平分布及不同工况下结构疲劳极限分布。根据上面的计算过程,可以得到疲劳应力水平和疲劳极限在服从正态分布的情况下得到参数估计值,计算结果如表4所示。图3和图4为疲劳应力水平和疲劳极限在服从正态分布时,用最小二乘法拟合曲线,分布拟合数据的相关性系数ρXY值均大于90%,二者为高度相关,也证明了假设的正确性。

表3 典型飞行状态下贮箱的应力水平和结构疲劳极限分布

图3 疲劳强度正态分布拟合

图4 疲劳应力正态分布拟合

表4 贮箱应力水平和结构疲劳分布参数
根据式(8)计算,β=1.3319,按无限寿命设计思想,10个典型飞行状态下贮箱的应力水平和结构疲劳极限分布,贮箱结构在无限寿命期内不发生疲劳破坏的概率为R=Φ(β)=90.86%。
2.3 基于疲劳损伤的可靠性分析
对贮箱结构进行可靠性分析,采用以疲劳损伤描述的可靠性分析模型。其主要思想是将结构瞬时疲劳损伤D(t)看成广义应力,临界疲劳损伤Dcr看成广义强度,从而实现以D(t)与Dcr的动态干涉来计算结构瞬时可靠度,如图5所示。结构D(t)与Dcr及分布则是建立以疲劳损伤描述的结构可靠性分析模型的关键[15]。

图5 疲劳累积损伤模型
据大量的实践经验,在名义应力相同的情况下,结构的疲劳寿命也会具有明显的分散性[16]。这就要求用处理随机变量的方法来处理疲劳寿命。结构的疲劳寿命设为N,对其取对数并记为X,通过对疲劳寿命理论分布的讨论可知,服从对数正态分布的疲劳寿命可以表示为
(14)
根据Miner线性疲劳累积损伤理论,结构瞬时疲劳损伤D(t)可以表示为
(15)
贮箱结构飞行t小时的可靠度R(t)可以表示为
R(t)=P[D(t)-Dcr<0]
(16)
目标概率密度函数为f(L1,L2,…,L10),设L1,L2,…,L10为10个相互独立随机变量,已知L1,L2,…,L10的分布类型和分布参数,要利用数学方法导出目标函数值的分布规律,往往由于积分困难而难于求解。本文采用Monte Carlo法来计算疲劳寿命可靠度。根据Miner疲劳损伤线性累积理论,考虑载荷和寿命的分散性,假设Dcr服从均值为0.45,方差为0.01的正态分布[17]。
Monte Carlo模拟法本质上是一种利用计算机通过抽样试验求近似解的方法,计算精度直接与模拟次数有关。根据计算精度要求可以利用上述方法选择模拟计算次数。对一般的工程技术问题,模拟次数M=3×106~5×106次即可满足工程精度要求。图6所示为以疲劳损伤描述的贮箱结构可靠性分析模型计算流程,利用名义应力法计算瞬时疲劳损伤度D(t)计算流程如图7所示。计算得到在整个飞行服役期内,贮箱结构在给定的飞行疲劳载荷谱作用下,其疲劳可靠度随飞行时间的变化规律,如图8所示。分析发现,在600飞行小时前,结构可靠度为100%,不会发生疲劳破坏,之后结构可靠度会迅速下降。因此,在假定的飞行疲劳载荷谱和采用的疲劳特性曲线下,贮箱结构不发生疲劳破坏需在600飞行小时内。

图6 疲劳损伤可靠性分析流程
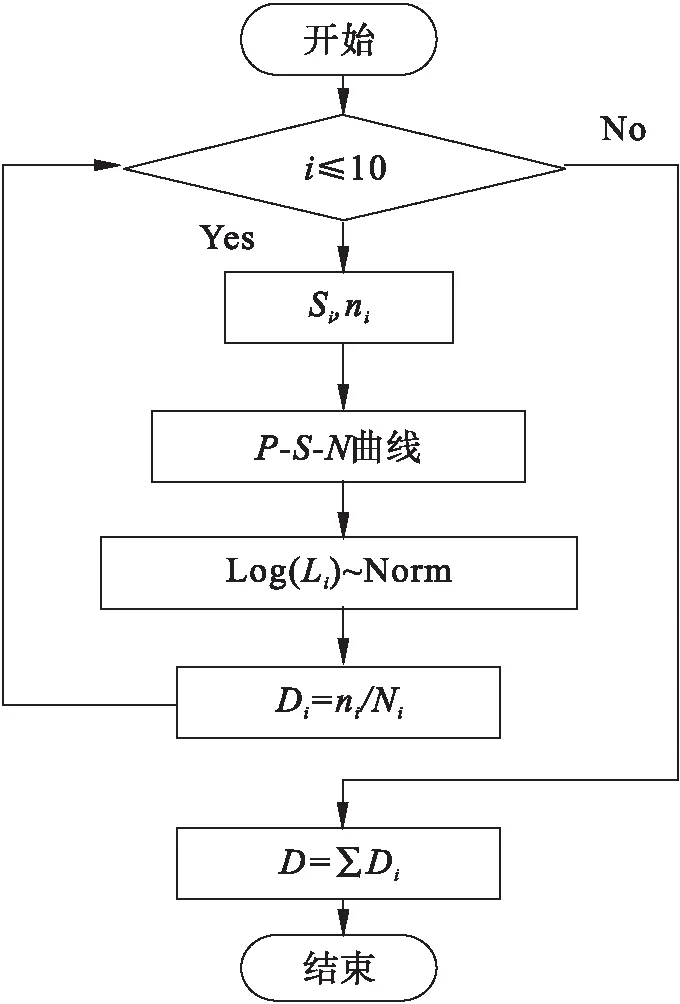
图7 疲劳损伤D(t)计算流程
3 结论
文章针对RLV低温贮箱结构在特定的飞行状态下的受载情况并结合有限元分析结果,分析了贮箱结构疲劳可靠性。
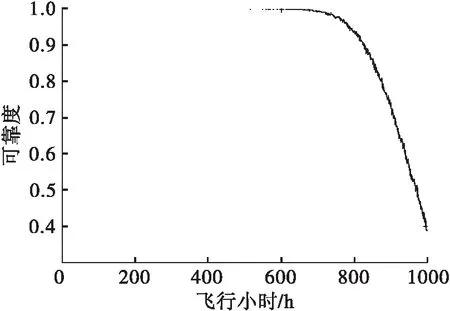
图8 贮箱疲劳寿命可靠度分布
(1)给出了各类载荷的统计数据,编制了结构的疲劳载荷谱,建立了低温贮箱结构的疲劳寿命可靠性分析模型;
(2)根据无限寿命设计的思想,利用应力-强度干涉模型,计算了贮箱在无限寿命期内不发生疲劳破坏的可靠度R=90.86%;
(3)根据Miner疲劳损伤线性累积理论,结合所设计的贮箱疲劳载荷数据和材料的S-N曲线,利用名义应力法计算出某一给定飞行时间的结构损伤和可靠度。
