基于结构化的课时整合教学
——以“植树问题”教学为例
2019-09-20夏向阳陆刚伟
夏向阳 陆刚伟
一、教材解读
人教版《数学》五年级上册第七单元安排了《数学广角》——植树问题,植树问题通常是指沿着一定的路线植树,这条路线的总长度平均分成若干段(间隔),然后讨论、揭示段数(间隔数)和植树的棵数之间的紧密关系。在现实生活中类似这样的植树问题还有很多,比如公路两旁安装路灯、花坛周围摆花、锯木头、架设电线杆等都属于这个范畴。本单元的具体教学内容安排四课时进行教学。
基于以上对教材意图的分析和比较,笔者认为将在一条线段上植树的三种情形(两端都要种、只种一端、两端都不种)和在封闭曲线上的植树问题分别独立展开教学,虽然可以更好地帮助学生理解不同的植树情形,建构植树问题的各种原始模型。但是,独立教学带来的明显弊端是割裂了不同植树情形的内在联系,缺乏从整体、全面的意识去建立完善的认知结构。因为,数学是一门系统、融合而富有严密逻辑结构的学科。完整的认知结构不仅有利于后续知识的形成和建立,同时能从整体的视角去解决实际问题,提高解决问题的综合能力。
二、教学实践
1.创设开放情境。

师:同学们在全长20 米的小路一边种树,每隔5 米种一棵,一共要种多少棵树?
生1:20÷5+1=5(棵)。
生2: 20÷5=4(棵)。
生3:我觉得上面两种都有可能。
……
【设计意图:植树问题的导入方式教师往往考虑的是学生更快地理解题意,直指解答。呈现的学习情境是确定性的(题目中就注明两端都种、只种一端、两端都不种)。其实,这样的导入方式容易束缚学生的思维,限制学生的想象,没有留给学生足够的思考空间和余地。物理学家阿基米德说:“给我一个支点,我可以撬动整个地球。”因此,在出示教学情境或学习材料时,应更多地体现开放性,赋予学生敢于自主探究、多元解答的机会,真正把学为中心落到实处。从课堂的实际教学反馈来看,这样的设计完全符合学生的认知基础和认知经验,学生有能力得出合理的问题解决。】
2.建立数学模型。
师:请20÷5+1=5(棵)这个算式的同学详细介绍你的思考过程。
生:我是这样考虑的,画一幅图进行表示,种一棵树隔5 米,再种一棵树隔5 米,一共要种5 棵。

师:结合20÷5+1=5(棵)这个算式,你能说一说你是怎么理解的吗?
生:小路一共20 米,每5 米一段,正好有这样的4 段,而4 段就可以种5 棵,从图上可以一目了然地看出。
师:段数我们在数学上也可叫做“间隔数”。
师:除了从图上数出间隔数和棵树之外,还有没有其他方法也能知晓间隔数和棵树。
生:我们也可以这样理解,种一棵树隔一个间隔,再种一棵树隔一个间隔,最后还多出一棵树。

师:你的想法真好,在数学上这种方法称为“一一对应”,运用“一一对应”的方法可以使间隔数和棵数之间的关系更明了。
师:20÷5=4(棵)这种想法的同学又是怎么理解的呢?
生:我是这样想的。假设最左边正好有一幢建筑物(比如房子等),那么用图表示是这样的:

师:这种情况,同学们觉得可能吗?
生:从图上我们就可以清楚地看出,段数和棵数是相同的。20÷5=4(段),间隔数有4 个,也就是种4棵树。
生:我们也可以用“一一对应”的方法来理解,一个间隔数对应一棵,再一个间隔数对应一棵,间隔数和棵数正好相等。

师:这位同学很会思考,运用“一一对应”的方法清晰地得出间隔数和棵数之间的关系。
生:老师,我突然觉得种3 棵数也是完全可能的。我是这样想的,既然最左边是一幢建筑物(房子等),那么最右边也有可能是一幢建筑物(房子等)。我用这样的一幅图进行表示:

生:我们也可以用“一一对应”的方法解释,一个间隔对应一棵树,最后还多出一个间隔。
师:我们的同学很会思考,很有想法,这是学好数学的关键。
师:通过刚才种树这样的一个情境,我们找到三种不同的结果。下面,你能把植树问题的各种情形进行整理吗?
生:两端都种——棵树=间隔数+1;一端种一端不种——棵树=间隔数;两端都不种——棵树=间隔数-1。
生:一端种一端不种,我们可以说成“只种一端”;“只种一端”就表示了一端种一端不种。
师:同学们的想法很好,“只种一端”更加简洁明了。
生:我们可以把两端都种、只种一端、两端都不种联系起来。
两端都种——棵树=间隔数+1;
只种一端——只要在棵树=间隔数+1 的基础上再-1,这样就得到了棵树=间隔数+1-1,也就是棵树=间隔数;
两端都不种也只要在棵树=间隔数的基础上再-1,也就是棵树=间隔数-1。
师:这位同学的整理很有想法,他把植树问题的三种情形进行了沟通和联系,这样便于我们理解。
【设计意图:为了掌握植树问题的三种不同情形,教材分别用例1、例2、例3 三个独立的例题展开教学,旨在让学生建立植树问题的三种不同模型。从教学成效来看,学生面对实际的问题时,通常只是停留在三种不同植树模型的表层,对其本质和内涵还没有真正建构。因此,如何让学生对植树问题的三种情形建立牢固的认知结构,是本节课的教学重点之一。当学生形成植树问题的三种情形时,教学没有戛然而止,而是及时让学生进行自主整理,打通三者之间的内在联系,提炼出完善的知识结构。同时,本节课另一个教学重点是让学生感悟重要的数学思想方法。教学时,笔者从实际问题入手,引导学生在解决问题的分析、思考过程中逐步发现隐含于不同的情形中的规律,经历抽取出数学模型的过程,体验数学思想方法在解决实际问题中的作用。本教学环节中,在无痕的教学过程中渗透了“一一对应、数形结合”等数学思想,激发学生对数学的好奇心和求知欲,体会学习数学的价值。】
3.灵活解决问题。
师:同学们,刚才通过观察、猜测、推理、验证等活动,我们学会了植树问题的三种不同状况,下面请同学们利用植树问题的本领来解决实际生活中的问题。
第1 小题:5 路公共汽车行驶路线全长12km,相邻两站之间的路程都是1km。一共设有多少个车站?

生:我觉得这个问题相当于植树问题中的“两端都种”,设立的车站相当于棵树,12÷1=12(个),12 个相当于间隔数。所以,用算式来表示是12÷1=12(个),12+1=13(个)车站。
师:这位同学很有数学眼光,敏锐地捕捉到设立车站和植树问题的紧密联系,从而进行合理解答。
请看第2 题:大象馆和猴山相距60m。绿化队要在两馆间的小路两旁栽树,相邻两棵树之间的距离是3m。一共要栽多少棵树?

生:我觉得这个问题相当于植树问题中的“两端都不种”,所以算式可以这样表示:60÷3=20(个),20-1=19(棵)。
生:我还有补充,应该还要加一步,19×2=38(棵),因为这道题目是小路两旁栽树,而不是只在一旁种栽。
师:你看得真仔细。请看第3 题:
一根木头长10m,要把它平均分成5 段。每锯下一段需要8 分钟。锯完一共要花多少分钟?

生:我觉得这个问题相当于植树问题中的“两端都不种”,锯的次数相当于植树问题中的棵树。所以,用算式可以这样表示:5-1=4(次),8×4=32(分钟)。
师:同学们真是火眼金睛,很快就能把问题看清楚。请看第4 小题:
张伯伯准备在圆形池塘周围栽树。池塘的周长是120m,如果每隔10m 栽一棵,一共要栽多少棵树?
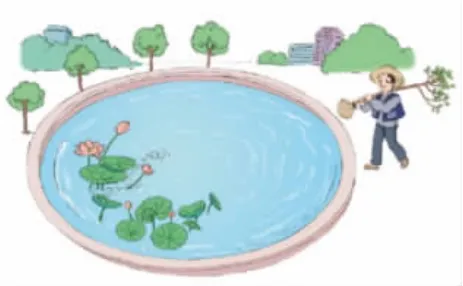
生:我觉得这个问题相当于“只种一端”,我们只要把圆形拉成线段就可以了。
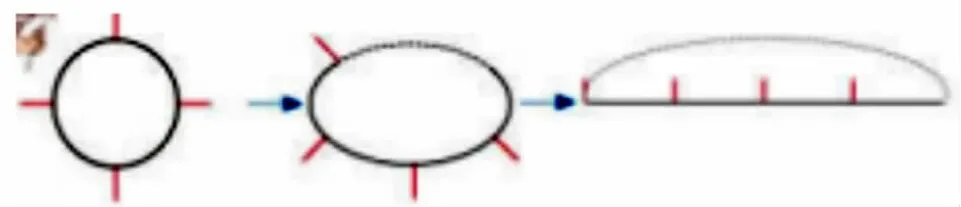
所以算式为:120÷10=12(个),也就是要种12棵树。
师:把圆形转化成线段,像这样的方法叫什么?以前我们在学习哪些知识时也曾经运用过?
生:这样的方法叫“转化”思想。我们在学习平行四边形面积计算的时候,就把平行四边形运用平移等转化成长方形。
生:我们在学习小数除法时,也是运用商不变规律把小数除法转化成整数除法后再进行计算。
【设计意图:掌握了植树问题的三种不同模型,并不代表会进行灵活运用和解决问题,特别是学生对三种情形容易出现混淆。如何让学生能够运用所学知识解决实际问题,需要教师有充分的认识。本环节的四道习题在选择的时候可谓独具匠心。第1 小题、第3 小题主要是让学生对植树问题的模型进行解析,把抽象的植树模型和具体的实际情境有机沟通起来,以此培养学生解决问题的应用意识。第2 小题是根据学生的最近发展区进行适度变式,让学生学会具体问题具体解答。第4 小题尽管是在圆形上种树,和在线段上种树具有明显的区别。可是,通过把圆形拉直成线段,就和“只种一端”的本质相同,用“转化”的思想把圆形上种树纳入“只种一端”的知识体系中,充实了植树问题的内涵。】
师:同学们,今天这节课我们主要学习了“植树问题”,你还想提出哪些问题呢?
生:我们学会了在线段上、圆形上植树。那么,如果在三角形边上植树又是怎样的情形?
生:如果在长方形、正方形边上种树又是怎样的情形?
生:在线段上种树的间隔就是距离,而为什么在圆上种树的间隔不是距离,是弧线的长度呢?
……
师:同学们提出的问题很合理、有挑战性,也很有研究、探讨价值,有时提出一个问题往往比解决问题更重要,希望同学们在学习数学的同时,也要积极、主动地提出一些合理的数学问题。
【设计意图:《数学课程标准》(2011 版)明确提出:运用数学的思维方式进行思考,增强发现和提出问题的能力,提高分析和解决问题的能力。把发现和提出问题摆到了和分析、解决问题同等的重要地位。在课即将结束时,笔者让学生结合今天的学习内容,提出一些问题,不断积累的问题意识是学生创新精神的种子,可以为培养创新型人才奠定扎实的基础。】
