电子束焊接熔池周期性波动的数值模拟

杨子酉,房玉超,何景山

(哈尔滨工业大学 先进焊接与连接国家重点实验室，哈尔滨 150001)

电子束焊接因为具有能量密度高、焊接速度快、焊后变形小、焊缝质量高等优点，被广泛应用于航空、航天、核能、交通运输及国防等高新技术制造领域[1-2]。如何得到高质量的电子束焊缝，成为人们关注的焦点。随着计算机能力的提升，数值分析逐渐成为人们研究熔池内部温度与流动情况的重要手段。

选择合适的焊接热源模型是进行高效准确的数值模拟的关键。由于高能束焊接存在匙孔效应，人们多采用双椭球热源模型[3]、高斯圆柱热源模型[4]、高斯旋转体热源模型[5]和双椭球与圆柱组合热源模型[6]等。虽然这些体热源和组合热源可以在一定程度上反映高能束在空间中的分布规律，但不能真正体现高能束与匙孔壁面相互作用的动态过程。近年来，高能束焊接熔池行为的研究取得了较大进展，主要包括：熔池温度场和流场耦合行为的研究[7-8]，匙孔形成过程的研究[9-10]，熔池驱动力的研究[11-13]，焊接缺陷的研究[14-15]等。但很少有研究者对焊接进入准稳态后熔池与匙孔的波动与震荡情况进行分析。

本研究基于Fluent软件，建立了电子束焊接三维瞬态模型，对非穿透焊接熔池进行了数值模拟。分析了电子束焊接进入准稳态后旋涡对熔池波动的影响，并采用动态面热源首次将焊接热源与匙孔形状进行耦合分析，总结出电子束焊接熔池的波动规律。本研究可以为深入了解电子束焊接熔池行为提供前提和基础。

1 有限元模型的建立

1.1 基本假设与控制方程

电子束焊接熔池流动非常复杂，计算时必须进行简化，故提出以下假设：(1)熔池中液态金属为不可压缩牛顿流体，其流动为层流；(2)忽略金属蒸汽和匙孔壁面之间的摩擦剪切力；(3)金属材料为各向同性，除比热容、热导率为温度的函数之外，其余材料参数皆为常数；(4)试件初始温度为300K。

在数值模拟中，焊接熔池要满足计算流体力学三大守恒方程，即连续性方程、动量守恒方程和能量守恒方程。考虑到电子束焊接的物理过程，在动量守恒方程中以表面张力、热浮力、重力和金属蒸汽反冲压力作为源项，在能量方程中以电子束热源、熔化焓和汽化焓作为源项。

1.2 边界条件与数学模型

图1为电子束焊接传热方式及受力过程的示意图。对于熔池而言，金属受高速电子束冲击而受热熔化，熔池表面金属迅速蒸发，以蒸发和辐射的形式进行散热；液态金属快速流动，在熔池中以对流的方式进行传热。对于未熔化的金属而言，主要以辐射方式进行散热，因为电子束焊接在真空下进行，所以不考虑工件表面对流换热。

电子束焊接过程中会产生匙孔效应，在匙孔壁面法线方向上，液态金属主要受反冲压力、液态金属静压力以及弯曲液面产生的附加压力作用；在匙孔壁面切线方向上，液态金属主要受表面张力所产生的切向力以及金属蒸汽与匙孔壁面摩擦产生的剪切力作用。在数值计算中，利用VOF算法追踪焊接熔池的自由表面。

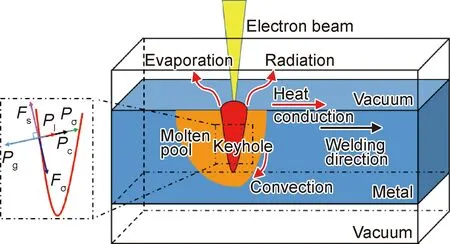
图1 电子束焊接示意图Fig.1 Sketch map of electron beam welding

在匙孔壁面上，电子束焊接热源采用高斯面热源，金属蒸汽反冲压力采用Semak提出的反冲压力模型[16]，它们分别为：

(1)

(2)

式中：qr是焊接热源能量密度；Q为电子束功率；R0是电子束聚焦半径；(x2+y2)为熔池中任意点距离电子束中心的径向距离；Pr为反冲压力；p0为标准大气压；ΔHv为汽化潜热；Tv为材料汽化温度；R为理想气体常数；T为热力学温度。

1.3 网格划分与材料属性

焊接熔池是热力耦合的结果，而金属的热物性参数对焊接温度场和熔池驱动力有着重要的影响[17]，因此材料热物性参数的选取十分重要。本研究采用10mm厚的2219铝合金进行电子束焊接，材料参数取自文献[18]。电子束加速电压60kV，电子束流15mA，焊接速率10mm/s，焊接方向沿x轴自左向右。模型尺寸为30mm×15mm×16mm，其中在金属板上、下各设置3mm的自由液面变化区域。利用ICEM对模型进行网格划分，在近焊缝区采用加密网格，在远离焊缝区采用疏松网格，最小网格尺寸为0.125mm，网格总数为771,120，节点总数为801,477，计算区域外围采用outflow边界条件。计算域初始温度300K，环境压力为0Pa。

2 电子束焊接熔池的周期性波动

2.1 焊接熔池温度场和流场耦合过程的分析

图2是电子束焊接过程中熔池纵截面和横截面温度场与流场随时间演变图，其中S和R分别代表表面张力和反冲压力所引起的流动。焊接初始阶段，母材受电子束轰击而迅速熔化形成熔池，液态金属温度继续升高到沸点而蒸发为金属蒸汽，其产生的反冲压力使熔池表面下凹，熔池产生R1和R2方向的流动，如图2(a)所示。从图2(b)，(c)中可以看出，随着匙孔深度的增加，匙孔底部的液态金属被金属蒸汽反冲压力向下压，形成R1方向的流动；随着匙孔深度和壁面面积的增加，匙孔温度上低下高，此时，匙孔壁面附近的液态金属沿着匙孔壁面向S1方向流动；在位于熔池表面的负表面张力梯度作用下，匙孔中的液态金属向后排，受到固液界面的阻碍而回流，形成S2方向的流动。在匙孔深度增加的过程中，匙孔底部的金属蒸汽反冲压力使液态金属向R1方向流动；R1方向上的液态金属受到固液界面的阻碍而改变方向，然后被匙孔壁面的表面张力牵引形成S1方向的流动； S2方向上和S1方向上的液态金属在熔池中部汇合，共同流向匙孔壁面，如图2(d)，(e)所示。

如图2(f)所示，随着焊接过程的进行，匙孔深度达到准稳态，但熔池体积仍在持续增大、熔池拖尾长度也在不断增加。在匙孔沿着焊接方向移动的过程中，不停地产生被匙孔排开的液态金属，由于匙孔的产生是一个由浅入深的过程，所以将被排开的液态金属可以分为两个部分：对于匙孔上半部分，液态金属向四周排开，产生S2方向的流动，流动到熔池边界的液态金属回流，并在匙孔壁面表面张力的牵引下形成S3方向的流动；对于匙孔下半部分，液态金属被金属蒸汽向下压，最终产生流经固液界面、最终汇入匙孔表面的S1方向的流动。S1和S3方向上的液态金属在熔池中间部位汇合，流向匙孔表面，紧接着再产生上述流动，周而复始。

0.8s之后，电子束热源继续移动，熔池流动行为与0.8s基本保持一致，改变的仅仅是熔池体积和熔池拖尾长度。图3是电子束焊接过程中熔池长度和宽度随时间变化曲线。从图3可以看出：焊接0.5s以后，熔池宽度趋于稳定；焊接1s以后，熔池拖尾长度趋于稳定，可以认为焊接过程从此刻开始进入准稳态。

图3 熔池尺寸随时间变化的模拟曲线Fig.3 Simulation curves of molten pool size vs time

2.2 焊接熔池中涡流的变化规律及其产生原因

熔池进入准稳态后，尽管熔池的尺寸和形状基本保持不变，但其仍然在小幅度震荡，说明熔池内部仍然处于一个周期性波动的状态。为了更好地研究熔池波动情况，提取焊接进入准稳态后，不同时刻熔池中的流线，如图4所示。从图4可以看出，匙孔前方熔池中的液态金属流向匙孔后方熔池，为匙孔后方熔池提供了液态金属。不难发现，匙孔后方熔池中存在涡流，这些涡流的大小和位置并不是固定不变的。

焊接进入准稳态后，在熔池上方的逆时针涡流并排存在，如图4(a)～(e)所示，这些涡流在熔池表面引起了波浪，波浪前进的方向为沿熔池表面向后。从图4(a)，(e)中不难看出，熔池下方存在一个较大的顺时针涡流。这个涡流在液态金属的牵引下，逐渐移动到匙孔壁面，如图4(b)，(f)所示。涡流有继续向匙孔移动的趋势，但受到匙孔壁面的阻碍而逐渐变小；涡流在撞击匙孔壁面的过程中，由于顺时针旋转，导致涡流中的液态金属流向匙孔壁面，涡流使匙孔壁面某一位置产生了一个大的凸起，阻碍了电子束与匙孔底部的直接作用，此时的匙孔处于坍塌的临界状态，如图4(c)，(g)所示。匙孔表面凸起的部位与电子束直接发生作用，受到向下的金属蒸汽反冲压力，并在表面张力的驱使下坍塌，如图4(d)，(h)所示。通过分析可知，熔池下方经历了两个循环：(a)～(d)和(e)～(h)。在两个循环中，熔池下方的涡流经历了4个过程：涡流的形成、涡流的移动、涡流与匙孔相互作用、涡流的破坏。

图4 熔池纵截面流线的演变过程(a)t=1.505s；(b)t=1.524s；(c)t=1.528s；(d)t=1.530s；(e)t=1.534s；(f)t=1.561s；(g)t=1.582s；(h)t=1.584sFig.4 Calculated streamlines from molten pool in longitudinal-section side views(a)t=1.505s；(b)t=1.524s；(c)t=1.528s；(d)t=1.530s；(e)t=1.534s；(f)t=1.561s；(g)t=1.582s；(h)t=1.584s

依照上述分析，可以根据熔池中液态金属的流动把熔池分为3个区域：匙孔前方(Zone Ⅰ)、匙孔后方上半部分(Zone Ⅱ)和匙孔后方下半部分(Zone Ⅲ)，具体分界线如图5所示。在熔池的3个不同区域中，液态金属呈现出不一样的流动情况，涡流的旋转方向和移动方向也不尽相同。通过文献[19]可知，当液体流动方向和流速大小迅速发生改变时，就有可能产生涡流，下面根据此理论对这些不同区域涡流的产生原因进行分析。

图5 熔池不同分区示意图Fig.5 Diagram of different zones of molten pool

区域Ⅰ是匙孔前方的熔池，由于电子束热源刚刚与之接触，因此该区域体积较小。电子束更多地与匙孔前壁面接触，以产生新的匙孔。匙孔前壁面上的液态金属受较大的反冲压力，使液态金属向下流动，越过匙孔底端，最终流向熔池后方，如图6(a)中的R方向。该区域的存在为匙孔后方熔池体积的稳定起到了重要作用。

在区域Ⅱ中，靠近熔池表面会有多个逆时针涡流产生，其形成过程示意图如图6(b)所示。该区域靠近熔池表面的液态金属在表面张力的作用下向V1方向流动，因受到固液界面的阻碍而回流(V2)；一部分液态金属在改变流动方向的过程中与沿V1方向迁移的液态金属相遇，另一部分流向S方向；沿V2流动的液态金属经历了固液界面的剪切摩擦后流速变小，小于V1方向的液态金属流速，因此会形成逆时针涡流。S方向上的液态金属一部分撞击了匙孔壁面而改变方向，向匙孔开口处流动，紧接着撞击熔池上表面而改变方向(V3)，汇入V1。液态金属流动方向的连续改变，形成了一个逆时针涡流。两个涡流在液态金属的带动下不断移动。

在区域Ⅲ中，区域Ⅰ的液态金属直接流入该区域。其中一部分液态金属由区域Ⅰ进入区域Ⅲ时，被匙孔壁面下方表面张力吸引，沿V1方向流动；另一部分液态金属沿固液界面流动较短距离后被匙孔壁面上方表面张力吸引，形成V2方向的流动；剩余大部分液态金属沿固液界面向熔池后方流动，与熔池上方向下流动的金属相遇，产生S方向的流动。匙孔壁面从下到上温度呈递减趋势、表面张力呈递增趋势，导致V1方向上的液态金属流速较V2大。这两个方向上的液态金属撞击匙孔壁面而迅速改变流动方向并相遇。由于液态金属流动方向的连续改变，并且V1方向上流速快，所以产生了顺时针的涡流。该区域的涡流形成过程如图6(c)所示。

图6 熔池不同区域涡流形成过程 (a)Zone Ⅰ；(b)Zone Ⅱ；(c)Zone ⅢFig.6 Process of vortex formation in different region (a)Zone Ⅰ；(b)Zone Ⅱ；(c)Zone Ⅲ

2.3 电子束与匙孔壁面耦合行为

从图4中可以看出，电子束焊接过程中，匙孔的形状并不是固定不变的。区域Ⅲ中涡流的移动使熔池变形，进而影响匙孔的变化，提取图4中熔池形状和电子束在匙孔壁面上的作用位置，如图7所示，图中灰色部分代表熔池，绿色部分代表电子束与匙孔的作用位置。不难看出，电子束主要作用在匙孔壁面凸起的位置上。对于匙孔前壁面：匙孔壁面上凸起的部位接收电子束的能量，温度的迅速升高使之产生蒸气反冲压力，由凸起变为凹陷，如此反复，匙孔前壁面的液态金属快速波动。对于匙孔后壁面：熔池的翻滚不断地阻碍电子束与匙孔后壁面下侧接触，使其温度低于金属沸点而不能稳定存在；在匙孔后方液态金属表面张力和凹液面附加压力的作用下，匙孔底部被液态金属补充。由于焊接热源以恒定的速度向前移动，电子束不停地挖掘新的匙孔前壁面，而匙孔后壁面也不断地被液态金属补充，这就造成了匙孔一直是倾斜状态，即匙孔底部具有一定的滞后性。

图7 电子束与匙孔壁面的相互作用 (a)t=1.505s；(b)t=1.524s；(c)t=1.528s；(d)t=1.530sFig.7 Interaction between electron beam and keyhole (a)t=1.505s；(b)t=1.524s；(c)t=1.528s；(d)t=1.530s

2.4 实验验证

由于在实际焊接时熔池的流动行为很难检测，因此，人们多采用数值模拟的手段来研究焊接熔池的动态过程，并用对比焊缝横截面形貌的方法来进行验证数值模拟的有效性[20]。本研究模拟的焊缝熔化线形状与实际焊缝熔化线形状对比如图8所示。从图8可以看出，模拟的焊缝熔化线形状与尺寸和实际焊缝熔化线接近，因此可以验证本研究的模拟结果是合理的。

图8 焊缝横截面试验与计算结果对比Fig.8 Comparison of simulated weld shape with actual weld joint morphology

3 结论

(1)综合考虑了电子束与匙孔壁面的耦合作用，建立了电子束焊接三维瞬态模型，对10mm厚2219铝合金的电子束焊接熔池周期性波动过程进行了数值模拟。

(2)焊接进入准稳态后，熔池尺寸并不是恒定不变的，而是在小范围内震荡，焊接熔池呈周期性波动。

(3)根据液态金属流动规律可以将熔池分为3个区域，其中在区域Ⅱ和区域Ⅲ会产生涡流。区域Ⅰ中的液态金属起到维持熔池体积稳定的作用，区域Ⅱ中的逆时针涡流起到维持熔池表面积的作用，区域Ⅲ中的顺时针涡流促进熔池坍塌，使匙孔变得不稳定。

(4)匙孔壁面上的电子束并不是均匀分布的，两者的相互作用使匙孔底部具有滞后性。