金属元素掺杂α-Fe(N)体系的电子结构及力学性能的第一性原理计算

2019-09-19刘香军杨吉春贾桂霄杨昌桥蔡长焜

材料工程 2019年9期

刘香军，杨吉春，贾桂霄，杨昌桥，蔡长焜

(1 内蒙古科技大学材料与冶金学院，内蒙古包头 014010；2 内蒙古科技大学工业技术研究院，内蒙古包头 014010)

N对钢材性能有着显著的影响，如强度、硬度均随N含量的增加而提高，韧性却不降低[1]。同时N还能提升高氮钢的抗摩擦、抗腐蚀能力[2-4]。由于常压下N在钢液中的溶解度很低[5]，通常采用高压充氮[6]和添加固溶金属氮化物的方法[7-9]来提高N在钢中的溶解度。但高压充氮对设备的要求高、成本大，因此添加固溶金属氮化物(如Cr, Mn, Mo和V等的氮化物)来提高钢中氮含量是一种经济合理的有效方法。

在实际研究中，要实现氮在钢液中固溶量的精确测定以及分布稳定性的控制较为困难。此外，由于实验条件的局限性，尚不能够精确表征N在高氮钢中的分布以及合金元素对N的影响规律。同时，固氮金属原子对氮和铁的相互作用机制及其对力学性能的影响鲜见报道。

基于密度泛函理论的第一性原理能够不受实验条件的局限性准确预测合金的电子结构与热力学信息，相比实验研究能更准确地反映材料的本征物性。研究发现[10-14]，通过第一性原理计算可以得到掺杂金属或C, N等小原子对不同结构Fe稳定性的影响，并可较为准确地探究不同原子在基体中的占位倾向，深入探索掺杂原子对基体稳定性的影响以及作用机理。

因此，本工作以高氮钢为研究对象，采用第一性原理计算掺杂金属元素对α-Fe(N)稳定性的影响规律；以元素周期表中位于Fe同一周期附近的6种金属Ti, V, Cr, Mn, Co和Ni为掺杂元素，探究金属氮化物在钢中固溶的稳定性、体系电子结构以及力学性能，研究具有不同半径和电子结构的掺杂元素在α-Fe(N)中的稳定规律。

1 计算模型与方法

本研究所有计算采用广义梯度近似(generalized gradient approximation,GGA)[15]中的PBE (Perdew-Burke-Ernzerh)[16]泛函方法，选取450eV的平面波截止能和4×4×4的MP-k(Monhkorst-Pack)[17-18]网格大小。自洽循环能量收敛设为1.0×10-4eV/atom，力收敛为0.002eV/nm。本工作研究了α-Fe(N)-M体系的稳定性、电子结构和弹性常数，所有计算由VASP程序完成[19]。

α-Fe晶胞具有体心立方结构，采用GGA-PBE方法获得的晶格常数为0.283nm，与实验结果0.287nm[20]及理论计算值0.282nm[21]几乎一致。选取2×2×2大小的超胞，见图1。在体心立方α-Fe中，N原子溶入八面体间隙所受到的阻力比溶入四面体间隙小，N易固溶在八面体间隙位置[22-24]，因此在本工作中，研究M(M=Ti,V,Cr,Mn,Co,Ni)原子在N原子固溶在八面体间隙的晶体结构模型中的占位情况。根据M原子与N原子的位置关系，本研究给出3种结构模型：M置换Fe1，其与N最邻近，即体心位置(BN)；M置换Fe2，其与N次邻近，即顶角位置(TN)；M置换Fe3，其与N不相邻(标识为NN)，见图1。

为了描述金属氮化物在α-Fe中稳定情况，使用原子间结合能来表示，计算公式[25]如下：

(EFeMN-NFeEFe-NMEM-NNEN)

(1)

式中：ΔΕFeMN为晶体的结合能；ΕFeMN为晶体的总能量；ΕFe,ΕM和ΕN分别为Fe,M和N孤立原子的能量，通过将其放置在1nm×1nm×1nm大小的晶胞格子中获得；NFe,NM和NN分别为单胞中Fe,M和N原子的数量。结合能越小，原子间的结合力越强，将需要更高的能量才能使键断裂，晶胞越稳定。

对晶胞结构进行优化后，晶格常数c略大于a，因此计算掺杂结构的力学性能使用满足四方晶系的相应计算公式。根据四方晶系力学稳定性判断条件：对于四方体系，独立弹性常数C11,C12,C13,C33,C44和C66必须同时满足公式(2)，晶体才能稳定存在。

(C11-C12)>0；(C11+C33-2C13)>0；

Cii>0 (i=1,3,4,6)

(2)

根据计算出的独立弹性常数，通过Voigt-Reuss-Hill[26]近似，可以进一步计算出各固溶体的体积模量B、剪切模量G和弹性模量E，计算公式见式(3)～(10)[27]：

M=C11+C12+2C33-4C13

(3)

C2=(C11+C12)C33-2C132

(4)

(5)

(6)

BR=C2/M

(7)

(8)

(9)

(10)

式中：BV和GV分别为Voigt近似下的体积模量与剪切模量；BR和GR分别为Reuss近似下的体积模量与剪切模量。

2 结果与讨论

2.1 几何结构

对掺杂M(M=Ti, V, Cr, Mn, Co, Ni)原子的α-Fe(N)体系进行结构优化，结果表明，体系的晶胞参数均发生了变化，见表1。本工作只给出各体系3种掺杂结构中具有能量最低体系的几何结构参数。从表1可以看出，掺杂体系ΔV均增大，且不同掺杂元素对体系晶胞参数变化的影响不同。与α-Fe(N)体系相比，对比Fe原子半径大的掺杂原子V, Cr和Mn，掺杂体系的ΔV几乎不变或者变小，这说明掺杂的V, Cr和Mn与相邻原子之间产生了较强的相互作用。对原子半径小于Fe的Co和Ni的掺杂体系，ΔV稍微变小，这说明掺杂的Co和Ni与相邻原子之间相互作用较弱。

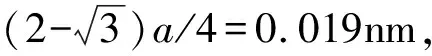
表1 α-Fe(N)-M稳定体系的几何结构参数Table 1 Geometric structure parameters of the α-Fe(N)-M stable systems

* The sum of covalent radius of Fe and N atoms orMand N atoms is given in the bracket.

2.2 结合能

为了研究这些金属原子在α-Fe(N)中的稳定性，本工作计算了M(M=Ti, V, Cr, Mn, Co, Ni)取代掺杂α-Fe(N)的3种可能结构的总能量。为进一步说明M取代掺杂体系的稳定性，本工作计算了3种取代掺杂中最稳定α-Fe(N)-M体系的结合能，并与α-Fe(N)体系进行比较，见表2。从表2可以看出，固溶合金原子改变了晶胞的结合能，其中，Ti和V的固溶减小了晶胞的结合能，这表明这些掺杂原子提高了体系稳定性；Cr, Mn和Ni的固溶稍微增大了晶胞的结合能，这表明这些掺杂原子降低了体系的稳定性；Co的固溶不影响晶胞结合能。从表2还可以看出，由于原子半径的不同，结合能有所差别，对位于与Fe同一周期的左侧金属Ti, V, Cr和Mn及位于与Fe同一周期的右侧金属Co和Ni，结合能的绝对值均随原子半径的减小而减小，且顺序为Ti>V>Cr>Mn和Co>Ni。

表2 α-Fe(N)-M稳定体系结合能和赝能隙Table 2 Binding energies and the pseudogaps of α-Fe(N)-M stable systems

2.3 态密度

为了揭示α-Fe(N)-M体系中原子间的相互作用情况，本工作计算了最稳定体系的态密度(density of states,DOS)和分波态密度(partial density of states,PDOS)与赝能隙，并探讨了M对α-Fe(N)电子结构的影响规律，见图2(图2中虚线表示费米能级)。

纯α-Fe在-54.5～-50.5eV的态来自于Fe3p电子，在-8.0～9.0eV的态来自于Fe3p3d4s的杂化电子，见图2(a)。掺杂N原子后，与N最邻近的Fe1在-17.0～-16.5eV能量区间产生来自N2s电子的新态，与Fe2及离N较远的Fe3相比，邻近N的Fe1在费米能级附近能量发生明显的离域化，且能量分布从原来的-5.0～3.1eV离域到-8.0～3.1eV，这表明N与Fe1原子在此能量区间发生了较强的相互作用，如图2(a)所示。掺杂金属原子Ti, V, Cr, Mn, Co和Ni后，与α-Fe(N)体系相比，α-Fe(N)-M体系除了来自由掺杂金属M引入的低能级杂质态，主要在-8.0～6.0eV能量区间有来自M3d和N2p电子的相互作用态，如图2(b)所示。

图2中费米能级两侧分别有两个尖峰，且尖峰之间的态密度不为零，这两个尖峰间的距离称为赝能隙，赝能隙越宽，共价性越强，因此赝能隙的大小可用于分析体系共价性的强弱。α-Fe(N)-M体系赝能隙见表2，从表2可以看出，掺杂原子M中仅Ti增强了体系的共价性，其他α-Fe(N)-M体系的共价性均被减弱。对位于与Fe同一周期的左侧金属Ti, V, Cr和Mn及位于与Fe同一周期的右侧金属Co和Ni，赝能隙均随原子半径的减小而减小，顺序为Ti>V>Cr>Mn和Co>Ni，这两个顺序规律以Fe为临界，类似于结合能规律。

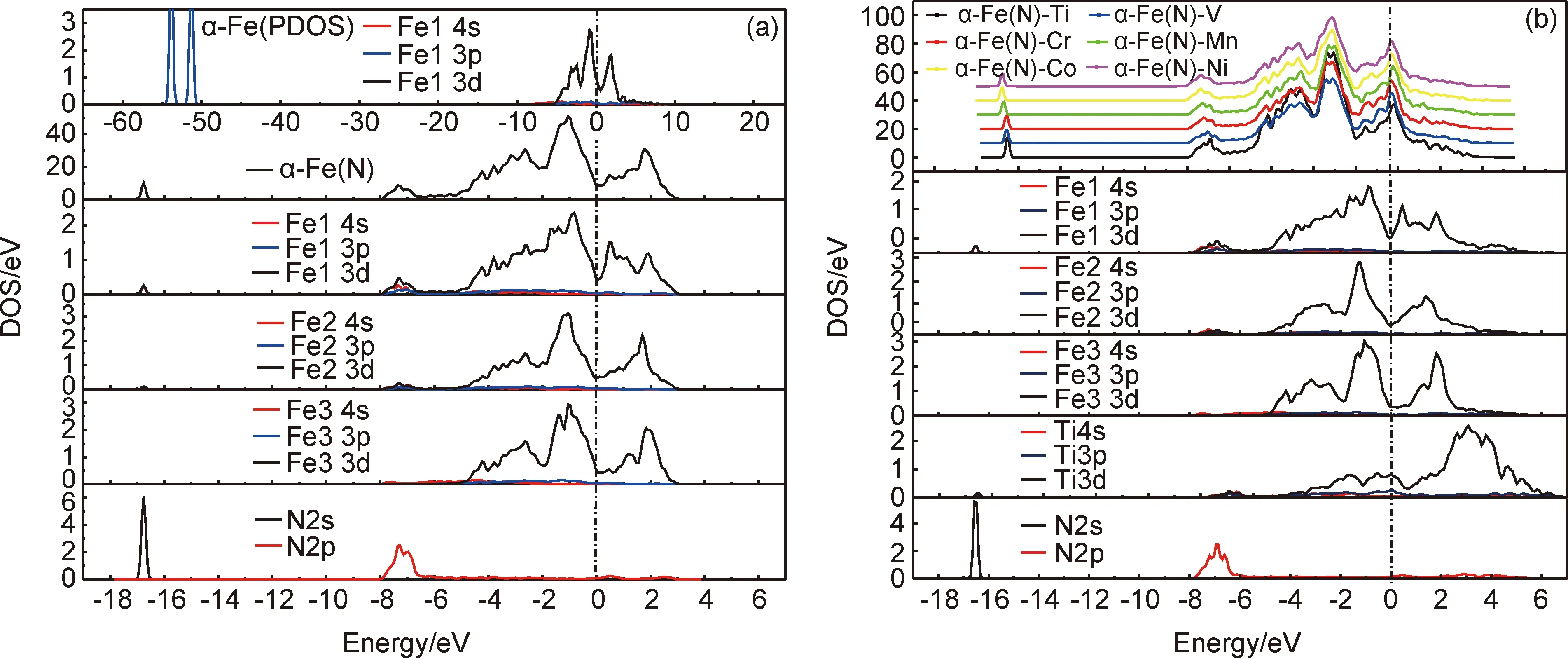
图2 Fe16,Fe16N体系(a)和α-Fe(N)-M体系(b)的态密度图Fig.2 DOS of Fe,Fe16N(a) and α-Fe(N)-M(b) systems

2.4 力学性能

对于各种掺杂体系，计算得到的α-Fe(N)-M体系C11,C12,C13,C33,C44和C66代入公式(3)～(10)分别获得各体系体积模量B、剪切模量G、弹性模量E及体现材料延展性能的B/G力学常数，见表3。

从表3可以看出，α-Fe(N)-M体系与纯α-Fe体系相比，剪切模量G和弹性模量E均得到提高，且分别提高了7.4%～11.7%和6.0%～9.8%，这说明与纯α-Fe体系相比，金属氮化物的掺杂提高了体系的刚度及耐磨性，这与掺杂金属元素和N之间形成很强化学键有关。与α-Fe(N)体系相比，剪切模量G和弹性模量E保持不变或略微减小，这说明与α-Fe(N)体系相比，金属氮化物的掺杂使体系的变形能力(剪切模量G)变差，材料的刚性下降，说明加入金属氮化物冶炼的高氮钢硬度低于充氮气冶炼的高氮钢。与纯α-Fe体系相比，除α-Fe(N)-Co体系外，体积模量B均不同程度地减小，但其下降幅度很小，仅为1.9%～4.1%。这表明，掺杂金属Co原子后，体系的不可压缩性最好。对体现材料延展性能的B/G常数进行了分析，与纯α-Fe体系相比，所有掺杂体系均不同程度地减小，减小了8.4%～14.3%，这表明金属氮化物的掺杂降低了材料的韧性。与α-Fe(N)体系相比，由于合金元素的掺杂使B/G不同程度地增大，这说明加入金属氮化物能够不同程度地提高高氮钢的韧性。从表3还可以看出，除了α-Fe(N)-Co(Co与N不相邻，Co不是有效的固氮元素)以外，掺杂金属原子V后体系的弹性模量E、剪切模量G和体积模量B均最大，这说明常压冶炼高氮钢时，添加V是提高钢材力学性能最有效的固氮元素。