山西原平ML4.7地震矩张量反演

李 斌，李自红，宋美琴，关鹏虎

(1.太原理工大学 a.矿业工程学院，b.地震与地质灾害防治研究所，太原 030024；2.山西省地震局，太原 030021)

北京时间2016年4月7日04时49分，在山西省原平市苏龙口镇(38.87°N，112.91°E)发生了ML4.7地震，震源深度11 km，山西原平、代县、定襄、太原、晋中、阳泉以及朔州等地震感明显。这是自2016年1月1日以来，继2016年3月12日运城M4.4地震、3月15日运城M3.0地震和3月27日运城M4.0地震后在山西省境内发生的第4次显著地震事件，也是2009年3月28日原平ML4.5地震打破山西地震带近5年的M4地震平静后在该地区发生的又一次显著地震。以往震例研究表明，山西地震带中强地震“南北迁移”活动特征明显[1-2]。此次原平ML4.7地震的发生，是山西地震带显著地震活动由南向北迁移的表现，对山西地震带中强地震具有重要的预警作用，预示着山西地震带可能进入了新一轮的4级地震活跃时段[3]。因此，深入理解此次显著地震事件的震源机制，有助于理解地震发生时震源区的应力状态与发震构造，以及山西地震带中强地震的孕育规律与活动特征，也是跟踪震情发展趋势的重要依据。

目前显著地震震源机制的求解方法较多，如P波初动法[4]、振幅比法[5]、P波初动联合振幅比法[4,6]、CAP全波形反演法[7-8]与矩张量反演法[9-11]等，且各种方法的研究结果都对世界上很多地震作出过较为合理的解释[12-16]。地震矩张量相比于其他方法，对于显著地震的震源机制解能有较为准确的描述[11]，且具有一定的优势。相对于P波初动与振幅比法，矩张量反演对台站布局要求低，且只需数字波形资料，无需进行震相分析，避免了人工量取震相误差带来的不确定性；反演结果反映的是整个破裂过程的信息，而非仅仅是初始破裂信息[17]。相比于CAP方法，矩张量反演方法的计算结果中含补偿线性矢量偶极 (CLVD)和各向同性分量(ISO)，因此地震矩张量可以分解为表示断层面剪切错动的双力偶分量(DC)、震源体膨胀或收缩的各向同性分量(ISO)、震源体优势方向的张裂或挤压变形(CLVD)等[9-10]。通常构造地震是由断层两盘的剪切位错触发，因此矩张量能更好地反映断层破裂信息[18]。

本文利用山西区域地震台网宽频带数字波形资料，在采用Hypo2000对地震重新定位的基础上，采用TDMT_INV时间域矩张量反演方法对2016年4月7日山西原平ML4.7地震进行矩张量反演计算，通过逐个增减参与反演的台站数量进行多次反演，结合震源机制随反演深度的变化特征进行参数的稳定性评价。将获得的震源机制结果与不同台站垂向分量的P波极性在震源球上的分布位置，以及与利用Snoke方法和CAP方法得到的震源机制解进行对比，以验证参数的合理性与可靠性。研究结果将有助于理解山西地震带中强地震的孕育规律与活动特征。

1 方法与原理

国内外学者对地震矩张量的求解方法进行了大量的研究。PATTON et al[19]首先将远震矩张量反演算法做了修改，进行了区域地震矩张量反演。DREGER et al[9]提出了在时间域利用区域地震波形(Pnl)进行地震矩张量反演的方法(time domain moment tensor inversion，TDMT_INV).本文采用的是DREGER于2003年改进理论波形计算方法后的TDMT_INV方法[10]，即在计算理论格林函数时加入了SAIKIA[20]改进的离散波数积分法。目前该方法在国际上已经得到广泛应用[21-24]。随着宽频带数字台网的建立，国内许多研究人员也利用该方法反演震源机制解：赵翠萍等[25]、唐兰兰等[26]、屠泓为等[27]将此方法应用于伽师震源区；王勤彩等[28]反演了汶川大地震余震序列88个地震的矩张量解。

TDMT_INV方法基于双力偶点源模型，在自由表面距离震源x处t时刻的实际观测记录dn(x,t)可表示为[29-31]：

(1)

(2)

式中：oi和si分别为观测数据与基于格林函数计算的时间域理论数据。VR的计算不仅考虑了波形的相似性，还考虑了绝对振幅的大小；VR值越大，表明波形拟合程度越高，求解出来的地震矩张量越可靠。在不同深度上搜索VR的最大值，以获得最佳震源深度与震源机制的最优解。

2 资料选取与数据处理

2.1 地震波形数据

目前，山西区域测震台网由72个实时记录与传输的数字化宽频带地震台站组网而成(山西省内台站57个，邻省台站15个)，基本上均匀分布于山西省及周边地区(图1(a)).现有台网条件下，ML≈2.0级及以上的地震，通常能同时被周围几十个台站记录到[32]。对于此次原平ML4.7地震，山西区域测震台网72个地震台站全部记录到此次地震，38个台站的垂向分量有清晰的P波初动。本文共选取了震中距120 km范围内8个台站的波形数据参与反演，台站方位及分布如图1(b)所示。选取数据的基本标准为：记录波形质量好，信噪比高，二阶Butterworth滤波器滤波后波形清晰，满足矩张量反演数据可靠性的要求。

HAVSKOV et al[33]研究表明，对于质量较好的波形数据，利用速度波形数据或积分至位移数据进行矩张量反演,其结果具有较好的一致性。本文在数据预处理过程中对比发现，速度波形数据在三个分量旋转及滤波后波形表现得更加稳定。鉴于此，本文选用了速度波形数据进行后续的反演计算。数据处理与计算过程主要包括：

1) 对原始波形数据进行去均值、去倾斜、去仪器响应的预处理。

2) 将3个分量分别旋转至垂向、切向和径向分量。

3) 选取二阶Butterworth滤波器进行滤波。频带范围的选取与震级有关；对于本次ML4.7地震，选取的频带范围为0.02～0.05 Hz.

4) 设定计算起始深度1.1 km(避免计算深度位于速度结构分层界面上)及步长1.0 km，基于区域速度结构等参数计算各台站不同深度范围的理论格林函数。

5) 进行矩张量反演及反演结果置信度评估。

图1 山西地震台网台站(a)及参与计算的8个地震台站(b)分布图Fig.1 Distribution of stations of Shanxi Seismic Network (a) and the 8 selected stations(b)

2.2 地壳速度结构

以往研究表明，无论哪种震源机制求解方法，地壳速度结构都是影响震源机制解的重要因素之一[17,24]。为了减少地壳速度结构对矩张量反演结果的影响，本文在Hpyo2000重新定位与矩张量反演过程中均采用了山西地震带最新的1D速度结构模型[34]，地壳分层及数据详见表1.

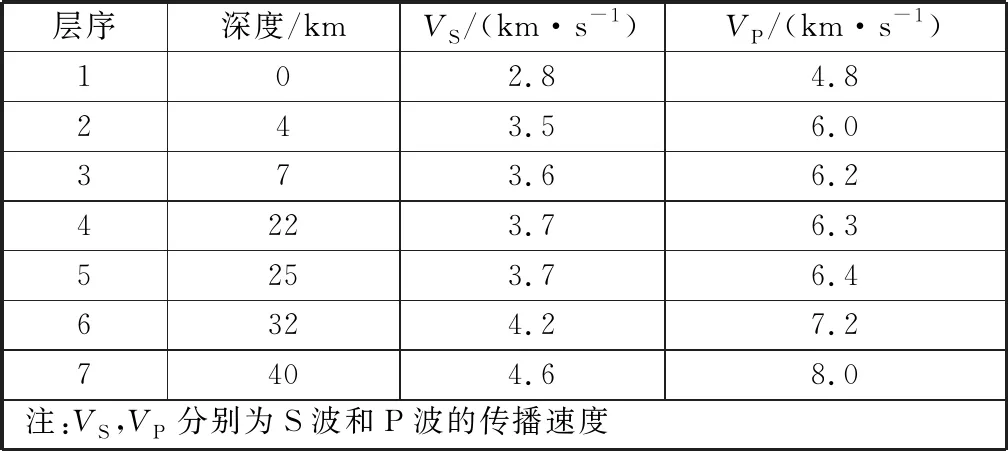
表1 本文计算采用的山西地震带1D速度结构模型Table 1 1D velocity model of Shanxi seismic belt applied in this study

3 计算结果与分析

3.1 重新定位结果

矩张量反演需要首先计算各参与反演台站的理论格林函数。除地壳速度结构外，震源位置特别是震源深度误差会对理论格林函数的计算结果产生影响，进而可能影响矩张量反演的最终结果，因此准确的定位结果是可靠矩张量反演的基础数据之一[6,17]。对于本次原平ML4.7地震，山西地震台网与中国地震台网均给出了定位结果，见表2.两个结果的震中位置基本一致，但山西台网给出的震源深度为11 km，中国台网为16 km，偏差较大。鉴于此，本文基于山西地震带最新的1D地壳速度结构，采用Hpyo2000[35]定位方法对本次地震进行了重新定位，得到主震震中位置为：38.86°N，112.92°E，震源深度14.7 km. Hpyo2000定位方法由Klein开发，采用传统的Geiger法基本思路，更适合于观测台站分布均匀的网内近震及地方震。重新定位结果将为后续矩张量反演提供保障。

表2 2016年4月7日山西原平ML4.7地震定位结果Table 2 Location of the Yuanping ML4.7 earthquake on April 7, 2016

3.2 震源机制结果

本文共选取了震中距120 km范围内8个地震台站记录的三分量速度波形数据进行地震矩张量反演。采用的滤波频带为0.02～0.05 Hz，起算深度1.1 km、步长1.0 km，共反演了1.1～25.1 km范围内不同深度的矩张量结果。根据反映观测数据与理论波形拟合情况的约化方差VR和Var/Pdc值随深度变化的情况，搜索出拟合程度最好、双力偶成分相对较高的解，即为最佳震源机制解。图2为矩张量反演过程中观测数据与理论波形最佳拟合情况下的反演结果。参与反演的8个地震台站中，除SHC台垂直分量和SHY台南北分量因波形有一定畸变在反演过程中被删除外，其余各分量的观测波形与理论波形的拟合程度尚好，平均VR=56.3%，结果符合信度要求[6,24,33]。

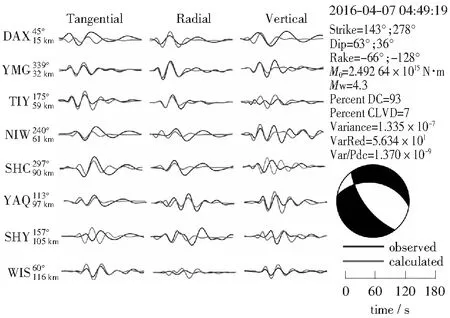
图2 山西原平ML4.7地震震源机制的波形拟合情况及矩张量反演结果Fig.2 Waveform fitting and results of moment tensor inversion of Yuanping ML4.7 earthquake

反演得到的最佳双力偶解节面I参数为走向143°，倾向63°，滑动角-66°；节面II走向278°，倾向36°，滑动角-128°；震源机制类型属于正断兼有右旋走滑分量。双力偶分量Percent DC=93，线性补偿分量Percent CLVD=7，震源机制符合双力偶点源的假设条件。主压应力P轴方位角为94°，倾角为64°；主张应力T轴方位角为216°，倾角为15°.标量地震矩M0= 2.492 64×1015N·m，矩震级结果为MW=4.2，与MS震级基本一致[3]。

3.3 震源深度的确定

图3是约化方差VR与震源机制解随不同反演深度的变化图。可以看出，随着反演深度的不断增加，震源机制结果逐渐从正断向正断兼有走滑分量、再向逆断趋势变化；但在5～16 km深度范围内震源机制性质及结果基本稳定，表现为正断兼有右旋走滑分量，且在11～14 km范围内VR相对稳定且取得最大值，为拟合程度最好、双力偶成分相对较高的解。因此，判断本次地震的最佳震源深度在11～14 km；这与重新定位结果的震源深度14.7 km具有一定可比性。

图3 约化方差VR随反演深度的变化Fig.3 Variance of variance reduction versus inversion depth

3.4 参数稳定性分析

影响地震矩张量反演结果稳定性的因素较多，如区域地壳速度结构、地震定位误差(特别是震源深度误差)、参与反演台站的个数、台站与震中的方位角误差，等等[17]。为进一步分析与验证反演参数的稳定性，在反演过程中我们首先对参与反演的8个台站，按每次增减一个台站进行反演；同时，基于Hypo2000重新定位结果，利用本区域最新的地壳速度模型进行了多次反演。具体反演结果详见图4.图4显示，在5、6、7、8个台站参与反演的情况下，最佳震源机制解节面I的走向最大偏差15°，倾角偏差8°，滑动角偏差10°.在参与反演台站数量减少的情况下，约化方差VR有所增高，但其余反演参数并未出现太大的变化。结合图3中5～16 km深度范围内震源机制性质基本稳定，及11～14 km范围内VR值稳定且取得最大值的结果，认为本文基于8个地震台站反演得到的参数基本稳定。

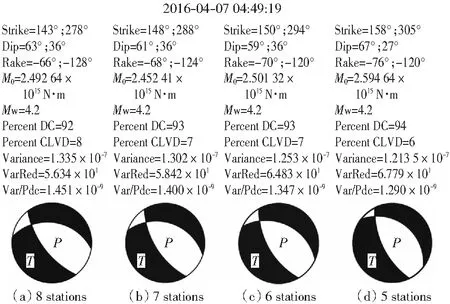
图4 不同数量台站参与矩张量反演时最佳震源机制解及其他参数的取值Fig.4 Focal mechanisms and other parameters from moment tensor inversion based on different stations

3.5 可靠性与误差分析

矩张量反演结果的合理性与可靠性通常可利用各记录台站垂直分量上的P波初动极性在震源球上的分布位置来分析判定。一般的做法是：首先利用区域地壳模型、震中距及震源深度计算记录台站的离源角；然后根据台站方位与离源角将其投影到震源球上，位于压缩区的P波初动向上，反之向下；通过考察P波极性与反演得到的震源机制解的一致性来验证结果的合理性与可靠性[18]。

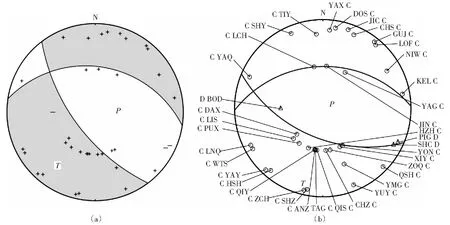
Strike=113°,Dip=53°,Rake=-74°,Source=Snoke图5 原平ML4.7地震的矩张量反演结果(a)以及基于P波初动的Snoke方法求解的结果(b)Fig.5 Focal mechanism of Yuanping ML4.7 earthquake by moment tensor inversion (a) and the focal mechanism result by Snoke method (b)

对于本次原平ML4.7地震，山西测震台网中共有38个地震台站垂直分量记录到清晰的P波初动，各个台站的P波初动极性及在震源球上的分布位置情况如图5(a)所示。除了少数几个台站外，其余32个台站的P波极性与基于8个台站波形数据反演得到的最佳震源机制解基本一致。

此外，为进一步分析结果的可靠性与可能误差，基于38个地震台站垂直分量记录的清晰的P波初动，利用Snoke方法求解了本次地震的震源机制断面解(图5(b))，并将矩张量反演得到的震源机制解与Snoke方法结果，及文献[3]利用CAP方法得到的解进行比较，具体震源机制解参数详见表3.可以看到：3种方法得到的震源机制解存在一定的差异，但震源机制性质一致，节面参数基本趋势一致，总体上具有可比性；存在差异的主要原因在于，3种方法的理论原理不同，逻辑算法及利用的数据类型不同，等等[33]。

表3 原平ML4.7地震震源机制参数Table 3 Parameters of Yuanping ML4.7 earthquake focal mechanism solution

4 讨论与结论

本文利用山西地震台网宽频带数字波形资料，在Hypo2000重新定位的基础上，采用TDMT_INV时间域矩张量反演方法，对2016年4月7日山西原平ML4.7地震进行了矩张量反演计算与参数的稳定性评价，并将获得的最佳双力偶解与利用Snoke方法及CAP方法得到的结果进行对比，验证了结果的合理性与可靠性。初步得到以下认识和结论：

1) 基于震中距120 km范围内的8个观测台站的波形资料反演得到的地震矩张量结果显示：最佳双力偶分量Percent DC=93，线性补偿分量Percent CLVD=7，震源机制符合双力偶点源的假设条件；节面Ⅰ参数为走向143°，倾向63°，滑动角-66°；节面Ⅱ走向278°，倾向36°，滑动角-128°；最佳震源深度11～14 km.主压应力P轴方位角94°，倾角64°；主张应力T轴方位角216°，倾角15°；标量地震矩M0=2.492 64×1015N·m，矩震级结果为MW=4.2，与MS震级基本一致。

2) 影响地震矩张量反演结果稳定性的因素较多，如区域地壳速度结构、地震定位误差(特别是震源深度误差)、参与反演台站的个数、台站与震中的方位角误差，等等。本文基于研究区最新的地壳速度结构，在Hypo2000重新定位的基础上，按逐次增减一个台站的方式进行多次反演，分析与验证了结果的稳定性，认为本文基于8个地震台站反演得到的参数基本稳定。此外，各台站垂向分量上清晰的P波极性在震源球上的分布与反演得到的最佳震源机制解基本一致。

3) 本文矩张量反演得到的最佳震源机制解与基于Snoke方法和CAP方法的结果存在一定的差异，但总体具有可比性。结果间存在误差的原因在于，不同方法的理论基础不同、利用的数据类型不同等。基于P波初动的断层面解反映的是初始破裂情况，而矩张量解能更好地诠释整个地震破裂过程。

致谢感谢山西地震台网中心为本研究提供地震波形数据。