基于粒子群的共振解调滚动轴承故障诊断研究*

毛海波，周凤星

(武汉科技大学 信息科学与工程学院，武汉 430081)

0 引言

滚动轴承作为一种常用机械部件，其状态的正常与否将直接影响设备运行状况。当其发生故障时，内圈、外圈、滚动体或保持架会出现剥落、磨损等损伤点，这些损伤点在转动过程中会产生冲击信号。早期故障因为冲击力微弱、工业现场噪声干扰严重等因素，常规的故障诊断方法效果有限，寻找有效的早期故障特征提取方法一直是该领域的热点和难点。

近年来很多学者对共振解调技术进行了研究，文献[1]针对共振解调技术受限于带通滤波参数的问题，提出了自适应共振解调技术，依靠对轴承信号的频谱分析确定振动信号固有频率。文献[2]研究证明软件共振解调技术和硬件共振解调是技术都能有效提取故障特征。文献[4]将轴承信号进行经验模态分解，根据固有模态函数的信息熵来选取带通参数。文献[5]研究了谱峭图在自适应选取带通滤波参数的应用情况。文献[6]把遗传算法用于自适应共振解调，以故障特征频率及二倍频和三倍频之间的差值和峰值比作为优化目标，在滚动轴承故障特征频率提取中取得了较好的效果，但遗传算法搜索速度慢、容易陷入局部极值点而且优化目标寻找复杂。基于上述研究成果，本文提出一种基于粒子群的自适应共振解调方法，以峭度和故障脉冲能量因子为复合指标，采用改进粒子群算法对带通参数进行优化，然后用最优带通滤波器对信号进行共振解调分析提取故障特征频率，完成故障诊断。

1 改进粒子群算法

粒子群算法具有实现简单、收敛速度快和优化结果准确等优点。粒子群算法中每个粒子根据适应度函数得到自己当前的适应值，然后根据群体和本身的历史状态信息，不断改变自身的速度和位置在N维搜索空间中搜寻最优解。其迭代搜索公式如下所示：

v(t+1)=wv(t)+c1r1(pbest-x(t))+c2r2(gbest-x(t))
x(t+1)=x(t)+v(t+1)

(1)

其中，v表示粒子速度，x表示粒子位置，w表示惯性权重，c1和c2表示学习因子，r1和r2表示扰动因子，pbest和gbest表示个体最优值和全局最优值。

1.1 混沌初始化

受种群粒子数量的限制，随机初始化得到的粒子不一定按照期望分布在搜索空间中，受文献[12]启发，利用混沌系统的随机性和遍历性，将混沌初始化方法引入到粒子群初始化中，使所有粒子遍历整个解空间，提高寻得最优解的质量。常见的一维混沌模型Logistic迭代公式如下：

x(t+1)=u(1-x(n))(x(n))

(2)

其中，x(t)∈[0,1]，u表示该混沌模型的控制参数，当u=4时，迭代结果为非周期时间序列，系统处于完全混沌状态。

混沌初始化具体实现步骤如下：先随机产生1个幅值都小于1的N维向量d0(d0,0，d0,1……d0,N)，根据式(2)迭代得到N个不同轨迹的混沌向量d1，d2……dn(n=1,2……N),通过映射公式：yn=ymin+dn(ymax-ymin)，将这N个混沌向量映射到寻优目标的取值范围内，其中ymax和ymin表示取值范围的上下限，再计算每个种群粒子的适应值，从中挑出N个性能较好的粒子个体作为初始粒子群。

1.2 随机权重

惯性权重w是粒子群算法的控制参数， 其值在很大程度上影响了粒子群算法的收敛速度和寻优结果。常用的线性递减惯性权重使算法在初期具有较强的全局搜索能力，后期具有较强的局部搜素能力，为平衡算法在搜索过程中的能力侧重，采用式(3)所示的随机权重代替线性递减惯性权重，任何时候算法都可以获得较大或较小的权重，使算法在整个搜索过程中都有较强的全局搜索能力和局部搜索能力。

w=wmin+(wmax-wmin)×rand(0,1)

(3)

1.3 动态学习因子

c1和c2分别表示粒子的自我学习能力和社会学习能力，当c1值较大时，有利于粒子搜索全局；当c2值较大时，有利于粒子加快收敛。因此设置动态学习因子为：

c1=cmax-(cmax-cmin)sin(90t/T)
c2=cmin+(cmax-cmin)sin(90t/T)

(4)

即c1递减、c2递增，来提高每个粒子在算法前后期的搜索能力侧重，其中T表示最大迭代次数，t表示当前迭代次数，cmax和cmin表示学习因子的最大值和最小值，根据试验取为2.05和0.15，此时粒子获得较佳的搜索能力。

2 自适应共振解调

滚动轴承常见故障类型可简单分为4类：内圈故障、外圈故障、保持架故障和滚动体故障，各故障频率特征值计算公式如下：

内圈故障：FBI=Z(1+d/Dcosα)f/2
外圈故障：FBO=Z(1-d/Dcosα)f/2
滚动体故障：FB=D(1-(d/D)2cos2α)f/2d
保持架故障：FT=(1-d/Dcosα)/2

(5)

其中，Z为滚子数，d为滚珠直径，D为轴承直径，f为轴承转频，α为接触角。

共振解调技术利用带通滤波器将调制了低频故障脉冲的高频共振信号提取出来，再通过包络解调得到低频信号频谱，根据多阶特征频率与理论故障特征频率对比确定故障类型。其诊断效果的好坏主要取决于带通滤波器中心频率和带宽的选取，一个合适的带通滤波器能够有效提取出故障特征频率。受文献[13]启发，本文采用分层思想，先根据峭度值确定带通参数的大致范围，再使用改进粒子群算法以故障脉冲能量因子为优化目标，自适应寻优得到带通滤波器的最佳参数。

峭度常用来检验信号偏离正态分布程度，对脉冲信号非常敏感，采用峭度作为指标能够有效提取出振动信号中的冲击成分，但峭度易受到轴承工作状态的影响，当故障加剧时，峭度指标就会失效，存在一定的局限性。为定量评价的滤波器参数的优劣，加入故障脉冲能量因子，定义为：

I=f2/E

(6)

式中，f表示包络谱中故障特征频率的幅值，E表示表示信号包络谱的平均能量值，I表示故障特征频率的能量与信号平均能量值的比值，其大小反映了带通滤波器滤波效果的好坏。I值越大则表明，滤波效果越好，故障特征越明显。整个自适应共振解调步骤如下：

如图5所示，基于流体力学理论，采用有限元方法，建立二维几何模型来模拟毫秒激光对铝板的打孔过程。为简化计算过程，对模型提出如下假设：1) 将计算中涉及的流体作为不可压缩牛顿流体处理；2) 将金属蒸气作为理想气体处理，且对于入射的激光无影响；3) 铝液的沸点不受其他因素影响。

(1)计算振动信号在不同中心频率带通滤波器下的峭度值，确定带通参数的大致范围。

(2)采用改进粒子群算法以故障脉冲能量因子为优化目标，在带通参数确定的可能范围内寻找最佳的中心频率和带宽，并将其视为最优带通滤波器。

(3)使用最优带通滤波器对振动信号滤波，并对滤波信号进行频谱分析，根据特征频率来诊断轴承状态。

3 数字仿真分析

为验证上述研究的可行性，设计故障仿真信号x(t)= (x1(t)+x2(t))×x3(t)+x4(t)。其中x1(t)是模拟故障频率为50Hz的周期性故障脉冲衰减信号，x2(t)是模拟频率为10Hz的轴承转频信号，x3(t)是模拟频率为2000Hz的高频固有振动载波信号，x4(t)为高斯白噪声。仿真信号时域图和频谱图如图1、图2所示。

图1 仿真信号的时域图

图2 仿真信号的频谱图

从x(t)的时域图中可以看出，故障信号被调制在高频载波信号中，受到背景噪声的干扰，模拟故障的周期性脉冲衰减信号淹没在其中，不能够直接得到周期衰减信号的频率；从x(t)的频谱图进行观察发现，高频载波信号十分突出，轴承转频信号和故障信号以差频的形式呈现频谱中，无法直接观察得到故障信号频率。

采用本文研究方法提取故障特征，首先根据峭度值选出一系列带通参数，将中心频率选择范围设为1kHz～3kHz，带宽为1000Hz，得到滤波后的信号峭度值如图3所示。

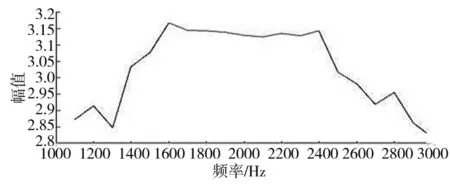
图3 不同带通滤波器滤波后的峭度值

从图3中可以看出带通滤波器的最优中心频率大致在1600～2400Hz范围之间，此时滤波信号的峭度值较大。采用改进粒子群优化算法以故障脉冲能量因子为目标函数进行带通滤波器的自适应寻优，取粒子个数50，最大迭代次数100，中心频率和带宽的寻优范围分别为1600～2400Hz和500～1000Hz，寻优结果如图4所示。

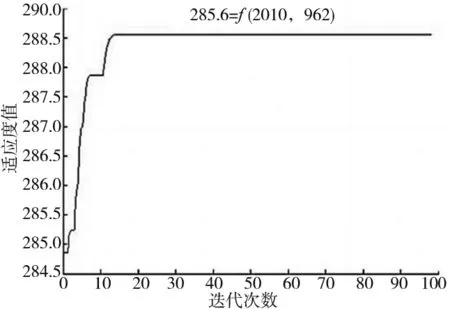
图4 粒子群寻优结果

当中心频率为2010Hz、带宽为962Hz时I值最大，将其作为最优带通滤波器，并对仿真信号滤波后得到包络谱如图5所示，可以明显地观察到频率为50Hz的周期性脉冲衰减信号，以及其二倍频100Hz和三倍频150Hz，因此该方法能够有效提取出数字仿真信号的周期性衰减冲击的频率。

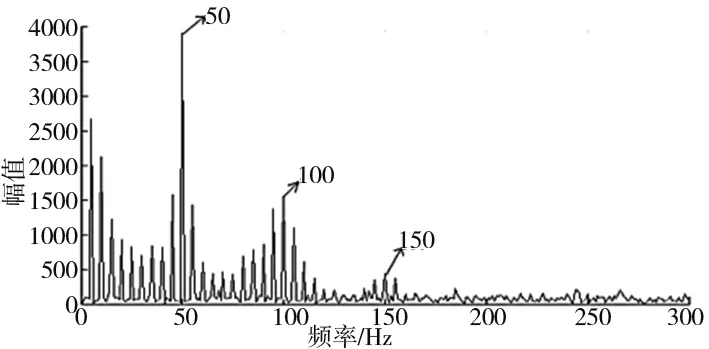
图5 仿真信号滤波后的频谱图

4 在滚动轴承故障诊断中的应用

实际故障信号诊断在QPZZ-Ⅱ旋转机械振动故障实验平台上进行，该平台能够模拟滚动轴承和齿轮箱的各种故障状态，故障轴承参数如表1所示。

表1 故障轴承参数

试验故障轴承转速为900r/min，根据故障频率计算公式计算得到该轴承的内圈、外圈和滚动体特征频率分别为107.1Hz、72.9Hz、38.1Hz。采样频率为20kHz，采样点数为65536，时域图和频谱图如6、图7所示。

图6 故障信号的时域图

图7 故障信号的频谱图

观察时域图可以发现，背景噪声强烈，轴承故障信号淹没在背景噪声中，分析其频谱，信号主要在中0～7000Hz这个频段，依据经验通常认为该信号的固有频率在2500～ 5000Hz，根据频谱采用中心频率和带宽分别为4000Hz和1000Hz的带通滤波器对该信号进行滤波，得到包络谱如图8所示，频谱上只能够明显地观察轴承转频15Hz，故障特征频率不突出，无法有效地提取故障特征频率，由此表明按照经验选取带通滤波器参数的方法具有明显的不足。

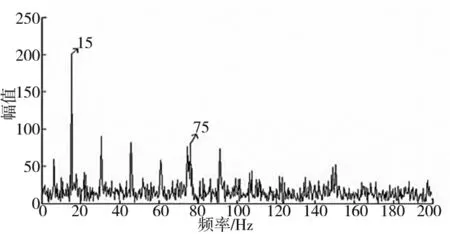
图8 常规带通滤波器滤波后的频谱图

采用本文提出的方法来确定最优带通滤波器，选择带通滤波器的中心频率范围为600～8000Hz，带宽为500Hz，得到滤波后的峭度值曲线如图9所示。

图9 不同带通滤波器滤波后的峭度值

根据峭度曲线，选择中心频率优化范围为5500～8000Hz，所需低频信号频率通常最大不超过1000Hz，选择优化带宽为100～ 1000Hz，以故障脉冲能量因子为优化目标进行粒子群算法自适应寻优，得到最优滤波器的参数为(5910,658.4)，滤波效果如图11所示，可以明显看到特征频率为74.5Hz，二倍频和三倍频分别为150.5Hz和225.5Hz，与理论值相比较可以确定为外圈故障，对轴承进行拆解也确定了故障类型为外圈故障。与按照经验确定带通滤波器方法相比，本文所用方法得到的自适应带通滤波器能够有效抑制背景噪声，准确提取出故障冲击成分，而且特征信息明显、准确。

图10 粒子群寻优结果

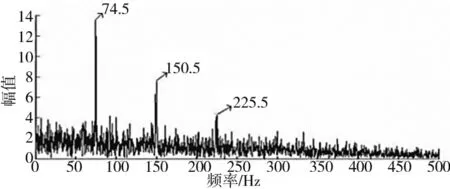
图11 最优带通滤波器滤波后的频谱图

5 结论

针对轴承故障早期振动信号微弱、检测困难的问题，本文提出了一种基于粒子群算法的自适应共振解调技术，采用峭度和故障脉冲能量因子作为优化指标，自适应优化得到最优带通滤波器，并采用合理的故障仿真信号和滚动轴承实际故障信号进行验证，结果表明该方法得到的带通滤波器能够有效提取出故障特征频率，而且该方法实现简单、诊断准确，在早期轴承故障检测中有明显的优势和使用价值。