微铣削切削力的解析模型分析*
2019-09-18喻春明汪小军迟玉红杨衍帅
喻春明,汪小军,迟玉红,杨衍帅,王 勃
(1.西京学院 机械工程学院,西安 710123,2.西安科技大学 机械工程学院,西安 710054;3.东北大学 机械工程与自动化学院,沈阳 110819)
0 引言
微铣削技术是一种成本较低的切削技术,可以直接加工出微小零部件或微小特征[1]。目前还没有统一的关于微铣削的定义,一般将铣刀直径小于1mm、零件尺寸在mm或μm范围、零件待加工尺寸小于1mm的铣削加工方式称为微铣削。
微铣削切削力的建模和预测对微铣削加工有重要意义,准确有效的切削力模型可以为加工提供参考,对避免刀具断裂和减轻刀具磨损有重要意义。微铣削切削力的解析建模大多是通过刀具瞬时切削体积来计算切削力的。Bao等[2]建立了刀具切削刃的运动轨迹,通过相邻两条轨迹的距离来计算瞬时切削厚度,然后计算瞬时切削力的大小。Bissacco等[3]考虑微铣削的尺寸效应切削力模型,该模型根据最小切厚和刀刃半径的比值修正了切屑的等效滑移面。张琢等[4]通过有限元方法,通过JC模型(Johnson-Cook material model),分析了不同刀刃半径对切削应力的影响。Park等[5]在考虑材料弹性回复的情况下,将微铣削切削力分为两部分:犁力主导区域和剪切力主导区域,并对包含犁力和剪切力的微铣削切削力进行建模。Afazov等[6]建立考虑径向跳动的微铣削切削力模型,通过大量的有限元分析,建立了微铣削切削力与瞬时切厚和切削线速度的非线性方程。Jin等[7]利用有限元和滑移线场的方法建立了微铣削切削力模型,将切削力表示为刀具几何参数和切削参数的函数,进行大量的切削仿真试验并将试验数据进行曲线拟合,以此来确定相关系数。Rodríguez等[8]考虑到微铣削刀具的细长结构在加工时会发生变形,利用材料弹性变形的准则建立了考虑刀具变形的切削力模型。张欣欣等[9]试验研究了加工参数对微铣削Al7075合金切削力的影响,发现进给速度对切削力大小的影响最为明显,然后是轴向切削深度和主轴转速。Lu等[10]在犁力模型的基础上,考虑轴向切削力,建立了微铣削三维立体切削力模型。Pratap等[11]利用ABAQUS,在考虑刀刃半径、热传导系数的情况下,进行了切削力有限元仿真。朱锟鹏等[12]根据微铣削加工机理出发,建立了包含径向跳动和刀具挠性变形的切削力模型。
然而,在已有切削力建模中没有考虑刀具磨损过程和刀具径向跳动的影响。本文提出一种模型,建立了包含刀具磨损和径向跳动的微铣削切削力模型。
1 动态切削厚度建模
微铣削过程与常规铣削过程类似,是一个断续切削的过程[9]。切削刃的运动轨迹取决于刀具半径、主轴转速、进给速度和径向跳动[10-11]。刀具径向跳动是铣削加工中普遍存在的问题。在微铣削中,刀具尺寸和加工尺寸较小,刀具径向跳动对加工的影响相对较大。微铣削刀具的第k个切削刃和第k-1个切削刃的运动轨迹见图1a。刀具径向跳动主要是由于刀具中心的偏移,见图1b。
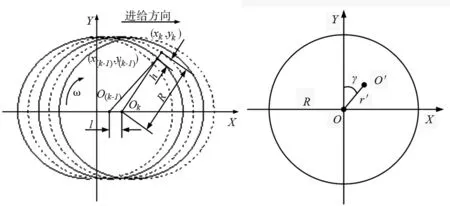
(a) 刀具运动轨迹 (b) 刀具偏移 图1 动态切削厚度示意图
(1)
其中,f为进给量,R为刀具直径,ω为主轴角速度,K为刀具总切削刃数,r′为径向跳动量,γ为径向跳动方向角。式(1)可以整理为:
(2)
同理,刀具第(k-1)个切削刃的轨迹可以表示为:
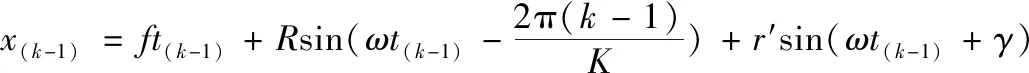
(3)
将式(3)带入到式(2)中,得:
F(t(k-1))=Rtan(wt(k)-2πk/K)cos(wt(k-1)-2π(k-1)/K)-
Rsin(wt(k-1)-2π(k-1)/K)-ft(k-1)+ft(k)+
r′tan(ωt(k)-2πk/K)cos(ωt(k-1)+γ)-
r′tan(ωt(k)-2πk/K)cos(ωt(k)+γ)-
r′sin(ωt(k-1)+γ)+r′sin(ωt(k)+γ)=0
(4)
式(4)为非线性方程,可以利用牛顿迭代法求解,为了求t(k-1),设初值为:
(5)
则
(6)

(7)
由图1(a)几何关系,动态切削厚度可以表示为:

(8)
其中,
(9)
(10)
x(O(k-1))=ft(k-1)+r′sin(ωt(k-1)+γ)
y(O(k-1))=r′cos(ωt(k-1)+γ)
(11)
x(O(k))=ft(k)+r′sin(ωt(k)+γ)
y(O(k))=r′cos(ωt(k)+γ)
(12)
切削厚度是一个动态量,径向跳动影响瞬时切削厚度。图2为双刃刀具的切削厚度实验记录(转速24000rpm,进给速度6mm/s,径向跳动角45°)。径向跳动导致两个切削刃的切削厚度并不一致;其差值与径向跳动量正向相关。当径向跳动量过大时,甚至导致一侧切削刃无法参与切削。
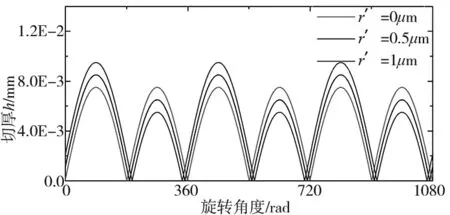
图2 双刃刀具的切削厚度实验记录
2 考虑刀具磨损的切削力建模
2.1 最小切削厚度
由于微铣削刀具尺寸较小,在切削力和载荷较大时容易断刀。故选择较小的进给速度,通常量级为μm。由于刀刃半径的存在,当切削厚度小于某一临界值时,产生较大的负前角。这时工件材料是通过刀具的挤压和犁削作用去除的,而不再是通过剪切作用。故切削厚度的这个临界值就是最小切削厚度。由于最小切削厚度的存在,在进行微铣削切削力预测时,传统的剪切力模型不再适用,还需要考虑犁力的作用。
2.2 犁力建模
当切削厚度小于最小切削厚度(hc)时,切削力主要为犁力,犁力计算通常采用弹性变形力模型。犁力的大小与刀具-工件的接触程度成正比。如图3所示,刀具-工件的接触程度可以用阴影部分的面积(Sp)表示,则:
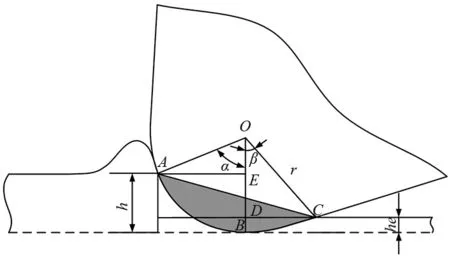
图3 犁力切削示意图
(13)
(14)
(15)
(16)
其中,r为刀刃半径,h为切削厚度,he为材料弹性回复,he=peh,pe为材料弹性回复率。
那么,当h≤hc时,切削力为:
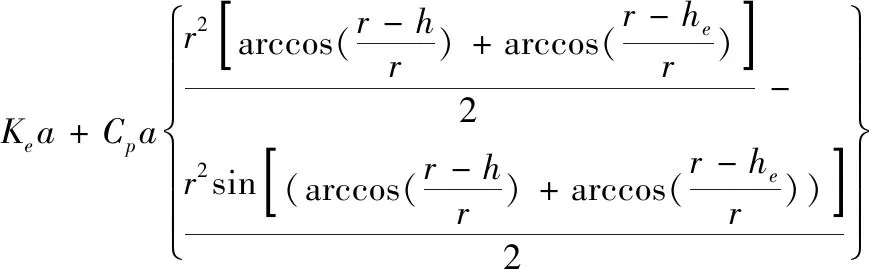
(17)
其中,a为轴向切削深度。
2.3 剪切力建模
当切削厚度大于最小切削厚度(hc)时,切削力主要为犁力和剪切力的共同作用,犁力和剪切力切削示意图见图4,微铣削切削示意图见图5。
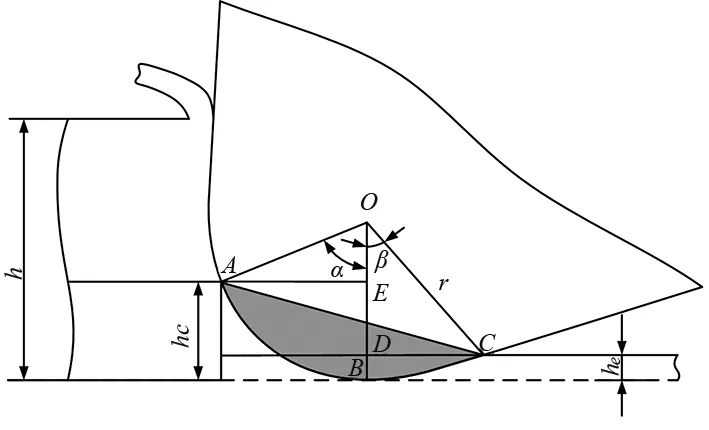
图4 犁力和剪切力切削示意图
此时犁力部分与前面类似:

(18)
剪切力可以按传统的剪切力模型计算:
Fc=Kcah+Kea
(19)
其中,Kc为切削系数,Ke为切削刃系数。
则当h>hc时,切削力为:
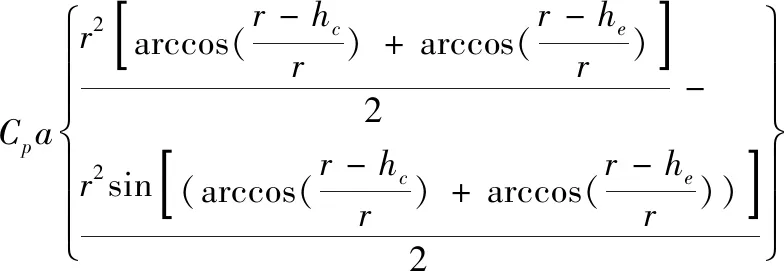
(20)
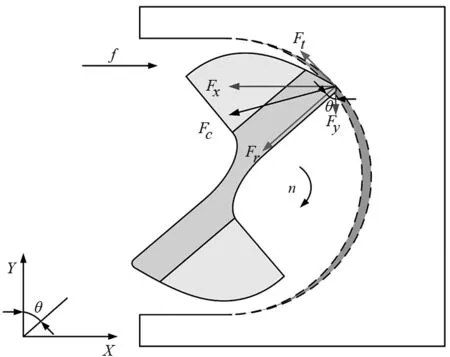
图5 微铣削切削示意图
综上所述,切向的切削力为:

(21)
转角为θ时,将切削力投影到X和Y轴可得:
Fx=Ftcos(θ)+Frsin(θ)
Fy=-Ftsin(θ)+Frcos(θ)
(22)
3 Deform-2D切削仿真获得切削力系数
在进行切削力计算时,需要已知最小切厚和切削力系数(Cpt,Kct,Ket,Cpr,Kcr,Ker)。为了获得切削力系数,利用Deform-2D切削软件仿真不同刀刃半径和不同切削厚度时的切削力,仿真流程如图6所示。
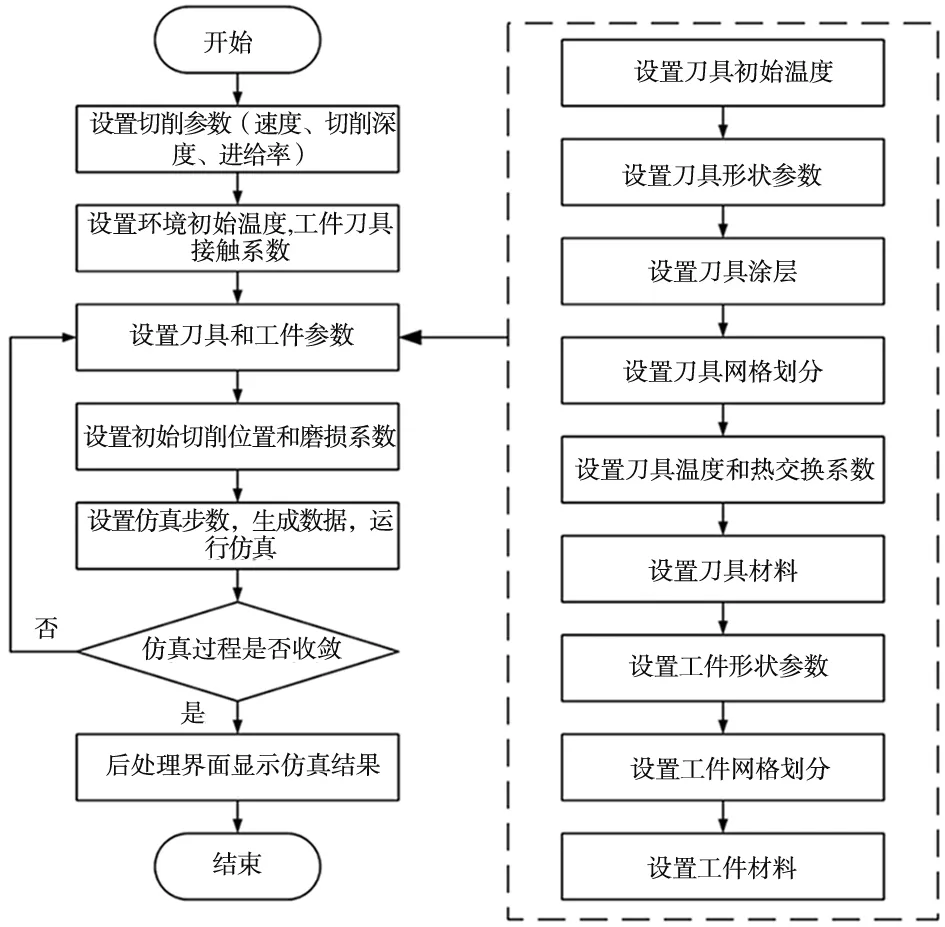
图6 Deform-2D仿真流程图
3.1 切削比能与最小切削厚度
切削比能E是指切削掉单位体积的工件材料所消耗的能量,可以通过能量消耗速率除以材料去除率获得,也可用切削力除以切削面积求得,即:
(23)
其中,P表示切削过程中能量消耗的速率;MRR表示材料去除率;v表示切削速度;b表示轴向切削深度;h表示切削厚度。
利用Deform-2D切削仿真,仿真不同切削厚度的切削力,并计算切削比能,设置刀具材料为硬质合金,工件材料为Al7075。刀具在x、y方向固定,工件在y方向固定,沿x轴向刀具运动。工件与刀具接触区网格高密划分,仿真模型示意图见图7。

图7 微切削二维仿真模型示意图
在仿真过程中,随着工件沿X轴运动,刀具与工件接触区网格自动高密划分。切削力仿真结果如表1所示,切削比能计算结果如图8所示。

表1 切削力仿真结果

图8 不同切厚的切削比能
由仿真和计算结果可知,切削比能随每刃进给量的增加而非线性减小。进给量从1μm增大到2μm时,切削比能迅速减小。因此,Al7075的最小切削厚度近似为0.2~0.5倍的刀刃半径。
3.2 计算切削力系数
为了获得切削力系数,利用Deform-2D切削仿真,仿真不同刀刃半径和切削厚度下的切削力,拟合切削力系数。仿真结果如表2所示。

表2 切削力仿真结果
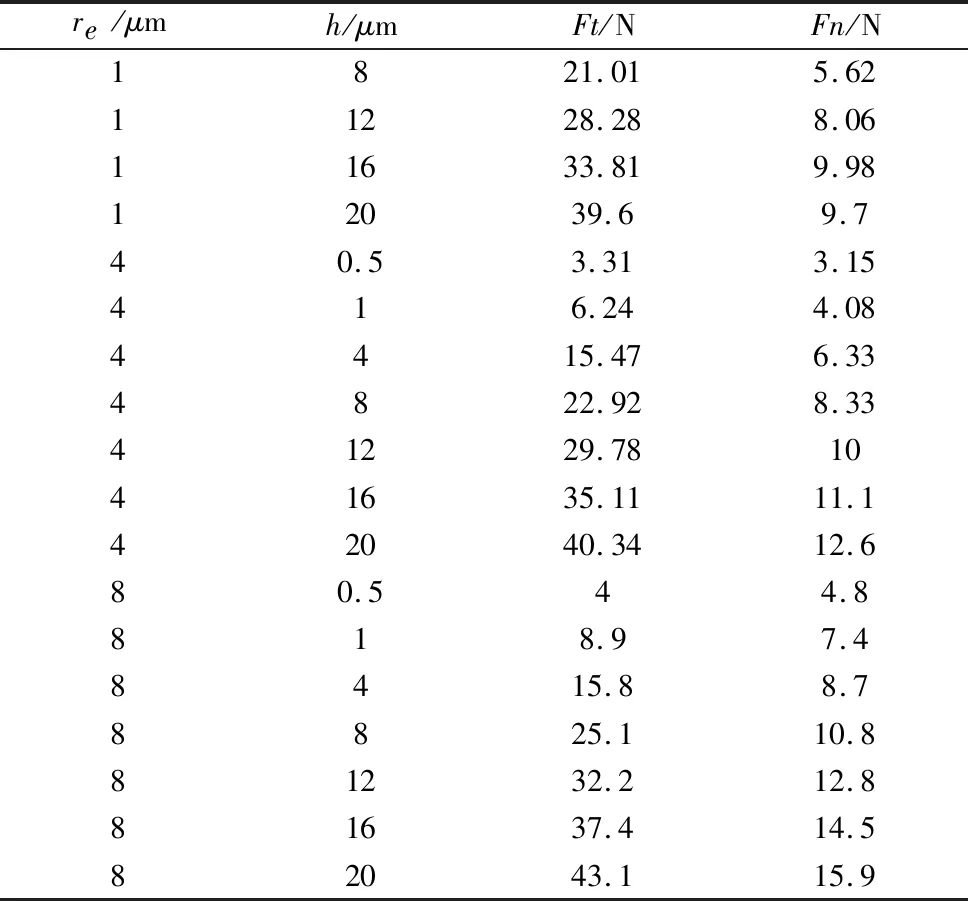
续表
根据仿真的切削力数据,利用Matlab拟合切削力系数和犁力系数,最小切削厚度与刀刃半径的比例介于5%~40%之间,根据切削比能的计算结果取hc=0.3re。弹性回复he=peh,pe为弹性回复系数,Al7075取pe=0.1,拟合结果见图9。
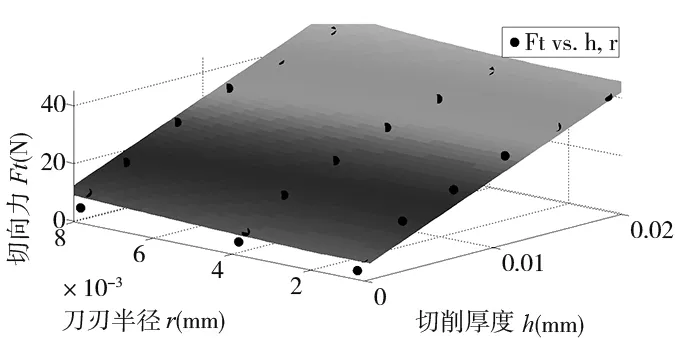
(a) 切向力
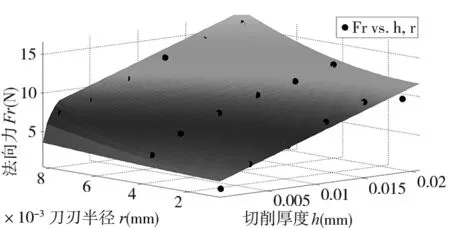
(b) 法向力 图9 拟合结果(●为仿真结果)
由拟合结果可得切削力系数和犁力系数如表3所示。

表3 切削力系数
4 切削力计算
切削力计算结果如图10和图11所示。刀刃半径增大会使切削力增大,且加速增大,而且X方向切削力的增速要高于Y向。刀具径向跳动使相邻两个切削刃的切削厚度不同;相应的,其切削力也不同。

(a) x方向力 (b) y方向力 图10 刀刃半径对切削力的影响(18000rpm,50μm,3mm/s)
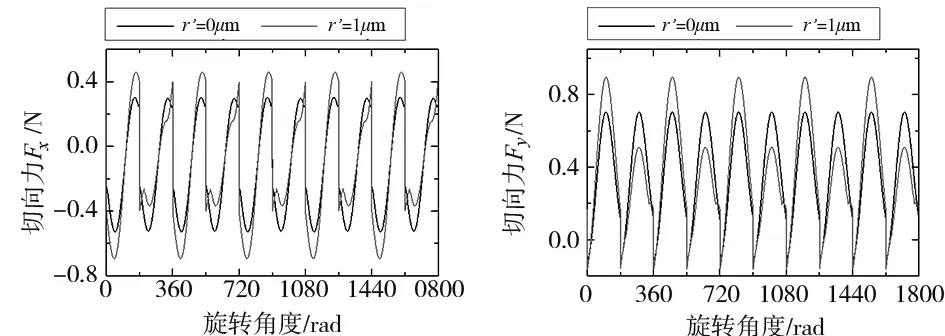
(a) x方向力 (b) y方向力 图11 径向跳动对切削力的影响(18000rpm,50μm,3mm/s)
5 切削力测试
通过切削力测试实验可检验切削力模型与测试结果的偏差。实验采用三向力传感器PCB260A01在MMT-50X微铣削试验平台上进行测试(因传统的三向测力仪带宽无法满足微铣削的高转速需求)PCB260A01需要安装在特定的夹具上使用。如图12所示,通过螺柱和螺母将基座、传感器和顶座连接,并为传感器提供一定的预紧力。基座可以固定在机床工作台上,工件可以固定在顶座上。

图12 切削力测试
测试选用的刀具为0.5mm硬质合金刀具(无涂层),45钢用于加速刀具磨损,获得不同的磨损程度,以缩短试验周期。主轴转速20000转/分,轴向切深50μm,进给速率5μm/tooth。时域采样点8192个,采样时间0.8s,时间很短故可忽略测试过程中的刀具磨损。结果如图13和图14所示:

(a) x方向力 (b) y方向力 图13 刀刃半径为2μm时的测试结果
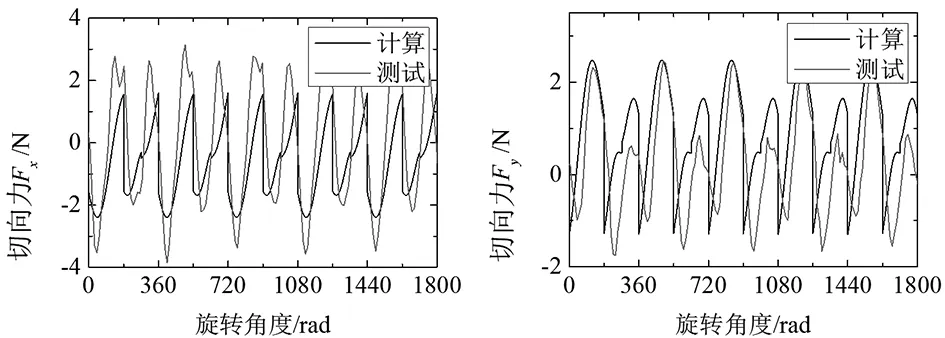
(a) x方向力 (b) y方向力 图14 刀刃半径13μm时的测试结果
故通过考虑刀具磨损的切削力模型可近似预测切削力的大小。测试与计算结果存在一定误差,原因可能有:
(1)模型忽略了刀具前角、后角和螺旋角的影响;
(2)模型只将刀具径向跳动简化到一个方向上;
(3)工作台的振动会影响测试结果。
6 结论
(1)建立考虑刀具磨损的微铣削切削力模型,将刀刃半径作为刀具磨损的评价指标,并建立包含刀刃半径的犁力模型。
(2) 通过Deform切削仿真,获得了犁力系数和剪切力系数。
(3) 通过切削力测试试验,获得不同刀具磨损程度的切削力,与切削力模型计算结果进行比较,验证了模型的正确性。
