工业机器人工作空间求解及逆运动学唯一解的确定*

2019-09-18刘曰涛沈宝民杨正娇

组合机床与自动化加工技术 2019年9期

刘曰涛，沈宝民，杨林，杨正娇

(山东理工大学机械工程学院，山东淄博 255000)

0 引言

机器人的工作空间定义为，不同关节运动所达到的末端执行器的所有位置的集合，该集合称为可达工作空间[1]。机器人的工作空间是研究设计机器人以及机器人应用过程中需要考虑的一个重要的问题。

目前用于研究机器人工作空间的算法主要有：几何绘图法、解析法以及数值法[2-10]，以上三种算法各有其优势。但是通过对现有机器人工作空间的求解算法对比研究发现，现有的关于机器人工作空间的算法大多太过于复杂，虽具有一定的研究意义，但实用性不强。本文基于MATLAB依据机器人工作空间的最基本算法对机器人结构进行简化，得出机器人工作空间的曲线图，与绘图法得出的机器人工作空间一致，由此证明了本算法的可行性。

同时本文还对机器人逆运动学进行了计算和分析，并确定了机器人逆运动学唯一解。机器人逆运动学就是通过已知机器人末端的位置及姿态，计算所对应的全部关节的变量，机器人逆运动学是机器人运动规划和轨迹控制的基础[11]。对于机器人逆运动学解的计算方法有很多，包括Paul提出的反变换法[12],Lee和Ziegler的几何法[13]，Pieper的方法[14]等。机器人正向运动学是给定各个关节变量之后，机器人末端位置和姿态是唯一确定的，而逆运动学一般具有多重解或无解，因此当出现多重解的情况下对于唯一解的确定就尤为重要。

本文采用的是比较普遍的反变换法求解，之后再通过筛选和条件限制确定唯一解。

1 机器人工作空间的计算

1.1 工作空间计算过程

本文以普通的6轴串联机器人为研究对象，机器人各个关节对其末端的位置和姿态的作用不同，前3个轴主要是实现末端的位置要求，被称为位置结构；后3个轴主要是实现末端姿态的要求，被称为姿态结构；机器人的工作空间的大小主要受位置结构的影响[15]。机器人工作空间设计时也是以第1、第2、第3轴及其所对应的臂长进行设计。对机器人工作空间计算时只需考虑机器人的前3个轴即可，为了提高机器人工作空间的直观性，甚至可以只计算机器人的第2、第3轴及其所对应的臂长，这样可以大大减小机器人工作空间的计算量提升机器人工作空间的求解速度。

本文所研究的6自由度工业机器人结构简图如图1所示。

图1 机器人结构简图

根据D-H算法给每一个关节赋予一个坐标建立参数表，如表1所示。

表1 D-H参数表

依据表1建立机器人D-H算法的齐次变换矩阵为：

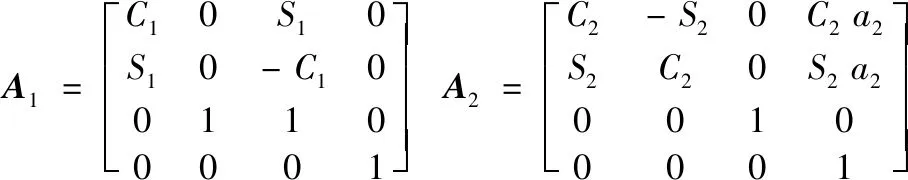
(1)

(2)

式中，Ci代表cosθi，Si代表sinθi。

式(1)、式(2)是以坐标系前置根据机器人参数建立的6自由度工业机器人数学模型，本文工作空间的计算主要是依靠坐标系后置所建立的数学模型进行计算分析。

由于本文求解的机器人工作空间是其剖截面图，即不考虑第一轴；在对机器人可达工作空间进行分析时不考虑第4、5、6轴姿态的条件，所以最终只考虑第2轴和第3轴及其所对应的大臂及小臂4个条件因素。

3T2=A2×A3=

(3)

Px=a3(C2C3﹣S2S3)﹢a2C2

(4)

Py=a3(S2C3﹢C2S3)﹢a2S2

(5)

Pz=0

(6)

因为本文只考虑了2轴和3轴，所以得出的是机器人工作空间的剖截面，故Pz=0。

根据机器人的结构特点和运动特性，存在如下条件约束：

(1)各驱动副转角范围。由于受到机器人机械臂上各零部件的影响和限制，机器人的大部分关节都有自己的转动范围，很难实现全周转动。通过了解现有的6自由度机器人确定第2第3轴的转角范围如表2所示。

(2)臂长。机器人的臂长越长其工作空间越大，但是为了适应不同的工作环境，需要设计不同臂长的机器人。

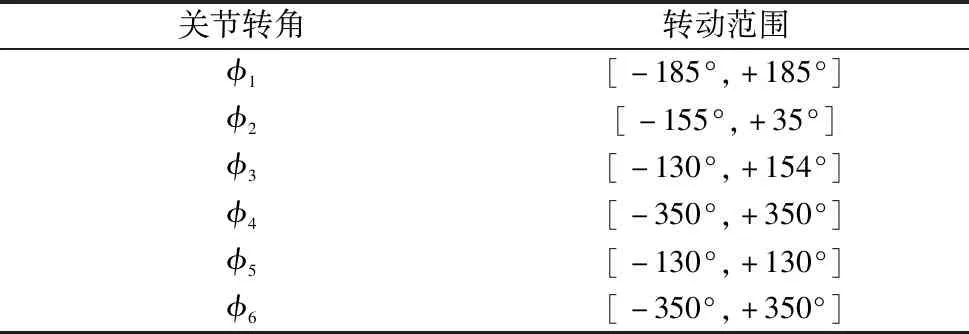
表2 机器人第2、3轴的转角范围

1.2 工作空间仿真与分析

用上述方法求(Px，Py)关于关节转角在φ2、φ3转动范围内所有点的集合，得到的仿真结果如图2所示。

图2 基于MATLAB生成的机器人工作空间图

图2是用本算法基于MATLAB生成的机器人工作空间图，图3是KUKA官方给出的机器人工作空间图。为了使本算法生成的工作空间图更具参考性和实用性，其参数和图3所示的机器人工作空间参数相同，是实验室现有的一台KUKA KR16型号机器人的参数。通过MATLAB生成的机器人工作空间图在X轴方向的尺寸为2636.3mm，在Y轴方向的尺寸为2406.6mm；而库卡官方给出的机器人工作空间图在X轴方向的尺寸为2638mm，在Y轴方向的尺寸为2412mm，两者在X轴方向上相差1.7mm，在Y轴方向上相差5.4mm，因为在对工作空间具体计算时，具体的参数和KUKA内部的参数存在一定的误差，并且KUKA官方承认所给的工作空间参考图外观尺寸并不是一个精确尺寸，由此可以确定通过此方法得出的机器人工作空间图和绘图法得出的机器人工作空间的剖截面图基本相同。同时证明了本算法对于机器人工作空间的计算以及描述具有重要参考意义。

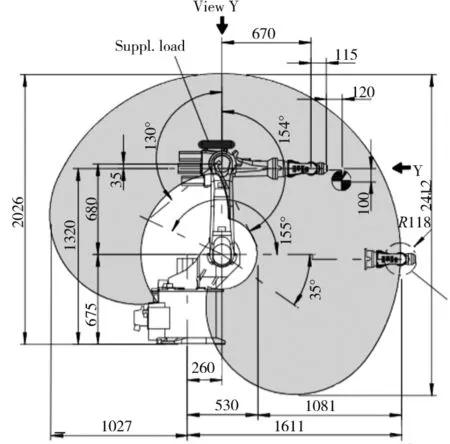
图3 KUKA给出的机器人工作空间图

2 机器人逆运动学解

2.1 机器人逆运动学解的计算

机器人逆运动学解对于机器人的重要性不言而喻，只有能够计算出机器人逆运动学解才能确定机器人每个轴对应的角度，进而使机器人到达期望的位置及姿态。对于机器人逆运动学解已经有比较成熟的算法，对于多个逆运动学解中唯一解的确定很少有文献给出明确的方法，本文提供一种对于6自由度工业机器人唯一解确定的方法。

首先，需要确定机器人的结构，根据机器人的结构按照D-H算法建立数学模型。为了便于后期的分析对比，同时也使得所建立的模型更加接近实际，本文按照实验室里一台现有的KUKA KR60-3型号的机器人建立数学模型。

表3 机器人参数

本文数学模型的建立和式(1)数学模型的建立不同，为了对机器人逆运动学解的计算更加简便而采用了坐标系前置，于是有：

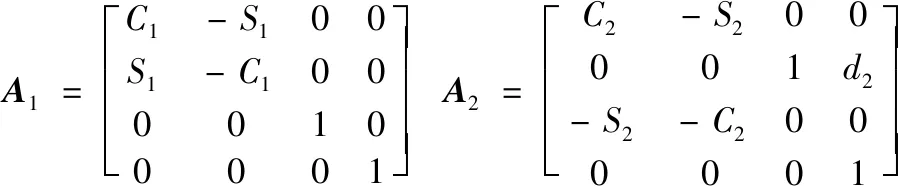
(12)

A=A1×A2×A3×A4×A5×A6

(13)

(14)

对于机器人逆运动学求解，根据式(13)进行计算，因为式(13)左侧矩阵各元素已知，即式(14)矩阵A中所有元素是已知的，而右侧的6个矩阵未知，Paul等人在进行反变换计算时是用未知的逆变换依次左乘式(13)的矩阵方程，把关节变量分离出来，然后求解未知变量[11]。

对于具体的机器人逆运动学解的过程这里不再详细描述，只介绍一下求逆解的步骤及结果：

(1)求解第一轴的反解。

用A1的逆矩阵左乘式(13)，经过整理以及三角代换后可得出θ1。

(15)

由于公式里存在正负号，所以一轴有两个解。

(2)求解第3轴的反解。

直接求解θ2因为参数不够无法直接求出，所以先求解θ3(求解θ3的参数是足够的，可以直接求出)，之后求解θ23即θ2+θ3的和，然后减θ3，最后得出θ2的具体解。

(16)

其中，

(17)

同样三轴也有两个解。

(3)求解第二轴的反解。

如上所述，这里首先求解θ23，然后减θ3，最后得出θ2的具体解。

θ23=θ2+θ3=atan2[-(a3+a2c3)pz+(c1px+s1py)
(a2s3-d4),(-d4+a2s3)pz+(c1px+s1py)(a2c3+a3)]

(18)

θ2=θ23-θ3

(19)

因为θ1和θ3各有两个解，有4种可能的组合，所以可以得到θ2的4种可能的解。

(4)求解第4轴的反解，在5轴角度不为0的前提下可解出4轴的唯一解(当五轴为0时即为奇异形位)。

通过上面对式(13)的依次左乘，θ4可以通过被左乘整理后的式(13)左右两侧参数的对应直接求出。

θ4=atan2(-axs1+ayc1,-axc1c23-ayc1c23+azs23)

(20)

(5)求解5轴的反解

θ5=atan2(s5,c5)

(21)

(6)求解6轴的反解

θ6=atan2(s6,c6)

(22)

在求解第4、5、6轴的反解时，第5轴在取得唯一解的同时也可取当前解的负数解，而同时第4轴和第6轴在当前解的前提下可以加180°，可取得相同姿态，所以一共有8个解。同时如果第4轴和第6轴的转动范围可达到将近±360°，则在最终姿态解上会更多，但是这并不意味着6自由度工业机器人的解已经超过了8个，而是多余的解是在我们限定的周期以外。

此时一个6轴工业机器人的6个轴的解已经全部计算完成，并且已经确定共有8个解，下一步需要对这8个解进行筛选以确定唯一解。

2.2 唯一解的确定

确定了机器人所有解以后，通过确定空间内两个不同点，即机器人从位置1到达位置2。本文可以对比大部分机器人在执行所有的程序之前为什么必须确定Home点，因为Home点是所有程序开始执行的第一个位置，也就确定了最原始位置的唯一解。为了对原理理解的更加简单清晰，这里假设Home点即为位置1，由此确定了位置1的唯一解。

对位置2求反解，前面已经确定位置2会有8个解，但是这8个解中首先可以排除4个解，即第一轴中在确定一个解以后，第二个解是首先确定的解加180°(只有当关节偏移为0时才是180°)。剩余的4个解可以继续排除2个，即通过第2轴和第3轴转动范围进行排除，因为机器人受机械的限制不可能每个轴都可以旋转360°，由此可以排除第2、3轴中转动角度较大的解。

最终只剩下两个解，而这两个解是第5轴取正负所取得第4轴和第6轴同原解相差180°的两组不同的解，由于之前确定了位置一的唯一解，由此判断在运动过程中使得第6轴转动最小的解即为最优解，由此确定了6自由度工业机器人逆运动学的唯一解(选择第6轴转动最小是因为考虑结合实际情况，当机器人末端到达下一个位置姿态时，使得机器人末端的动作尽量的小)。

以上所有分析均为机器人工作位置二不在奇异形位，第4和第6轴未超出其转动范围的前提下。当第4轴和第6轴有一个轴超出其转动范围时，可以选择使第5轴取原解的负数，同时判断第4轴和第6轴是正向超出其转动范围还是负向超出其转动范围，由此选择在原来的基础上加或者减180°。

本文按照实验室现有的一台KUKA KR60-3型号的机器人参数建立模型，以便于能够和现实情况进行对比，即a1=350mm、a2=850mm、a3=145mm、d2=0(指的是二轴的关节偏移和三轴的关节偏移总和为0)、d4=820mm。本算法通过MATLAB仿真和KUKA实际运动走相同的一段路径，通过KUKA研发的一款名为mxAutomation软件对KUKA所经过的路径的点进行记录，之后同样通过MATLAB生成路径曲线。

图5是通过本算法对机器人行走的一段路径的仿真曲线和通过记录KUKA行走的一段路径的点之后仿真出的路径曲线，两者起点和终点坐标完全相同。

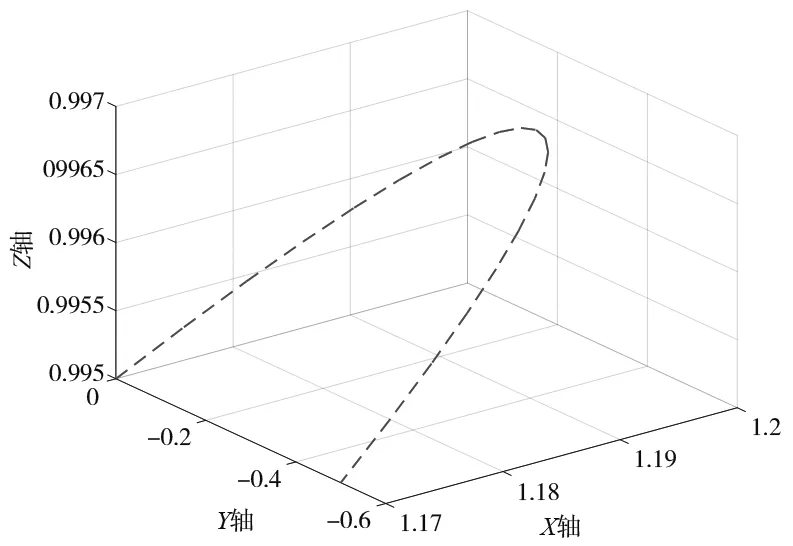
(a) 沿Y轴方向MATLAB仿真图

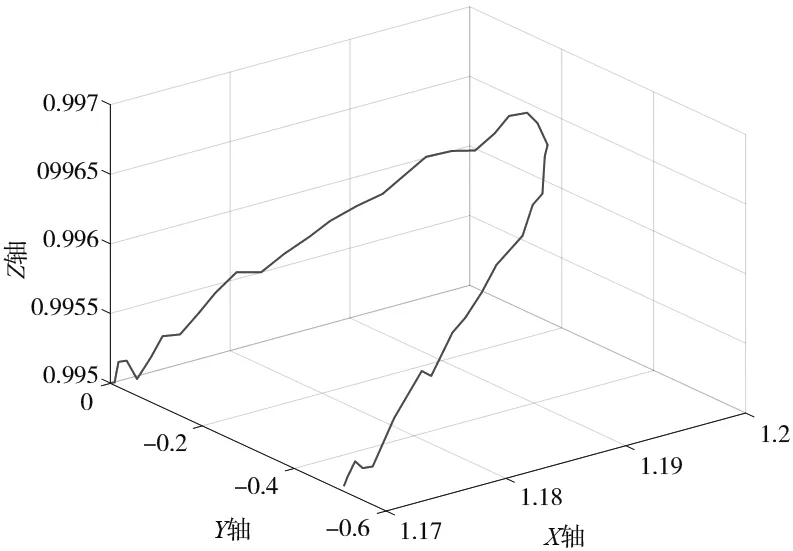
(b) 沿Y轴方向KUKA实际路径图

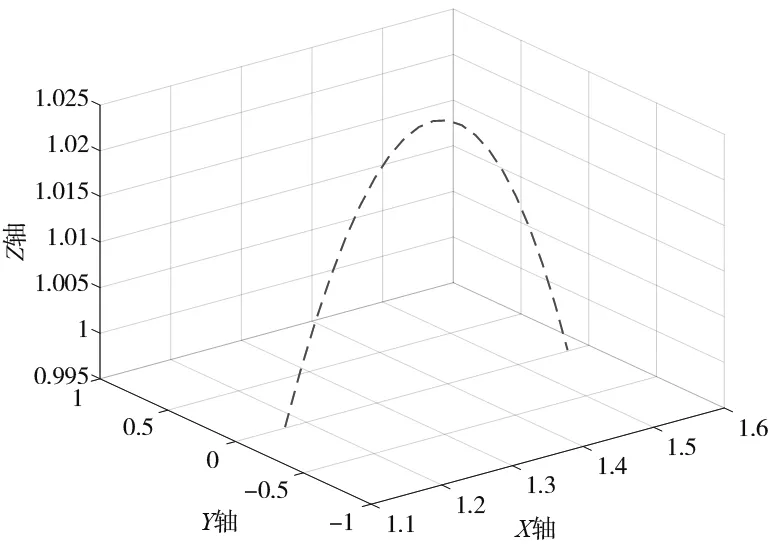
(d) 沿X轴方向MATLAB仿真图

(e) 沿X轴方向KUKA实际路径图

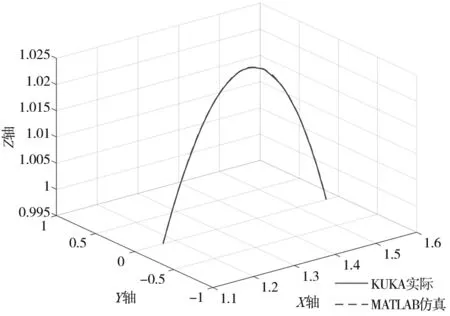
(f) Y轴方向下仿真与实际路径对比图

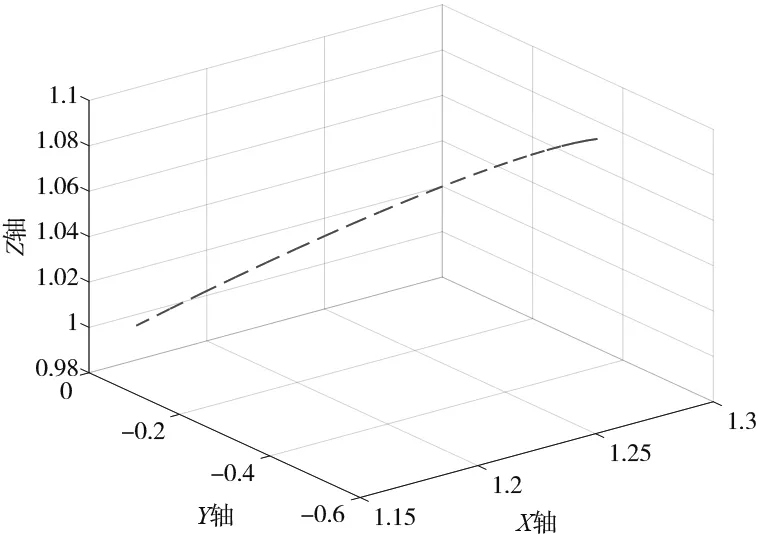
(g) 沿斜线方向MATLAB仿真图

(h) 沿斜线方向KUKA实际路径图

(i) 沿斜线方向仿真与实际路径对比图图4 MATLAB仿真路径及KUKA仿真路径

图4中的9幅图分别进行分析比较：

(1) 图4a、图4b是沿Y轴方向坐标为(1.17,0,0.995)、(1.17,-0.5,0.995)。图4a是本算法通过MATLAB仿真生成的路径图；图4b是MATLAB记录的KUKA实际路径的仿真图；图4c是将两者的路径放到一起后进行的对比。由图4b可以看出KUKA机器人在沿Y轴移动的时候存在一定的抖动，路径并没有MATLAB仿真出的理论路径圆滑，同时也可以由图4c看出，两者基本重合。

(2) 图4d、图4e是沿X轴方向，坐标为(1.17,0,0.995)、(1.57,0,0.995)。图4d是本算法通过MATLAB仿真生成的路径图；图4e是MATLAB记录的KUKA实际路径的仿真图；图4f是把两者的路径放到一起进行对比。由图4f可以看出对比，可以看出两者几乎没有区别。

(3) 图4g、图4h是沿一条斜线坐标为(1.17,0,0.995)、(1.27,-0.5,1.095)。图4g是本算法通过MATLAB仿真生成的路径图；图4h是MATLAB记录的KUKA实际路径的仿真图；同样图4i也是将两者路径放到一起进行对比，可以看出两者基本完全重合。

三种情况下姿态均保持不变，本算法是在笛卡尔坐标系下点到点的运动计算，KUKA也是在其工具坐标下执行的PTP(点到点)的命令。通过对比可以确定两者路径相同，在执行点到点的命令时都不是一条直线而是一段弧线。由此可以确定本算法对于机器人唯一解的确定具有重要的参考价值。