高中数学试卷讲评教学的几点思考
2019-09-17阚久义
阚久义


[摘 要] 学生答卷情况的全面统计能使教师对学生的答题情况获得准确的了解,教师应根据学生的错误情况进行知识、方法的及时梳理,使学生在针对性的讲评与反馈练习中获得错误的修正、“双基”的提升、思维的发展.
[关键词] 错误;知识;方法;目标;主线;反馈练习
测试在高三数学复习教学中的比重众所周知,单元测试、章节测试、综合测试、专项测试等各种形式充斥着整个高三数学复习教学阶段. 测试后的试卷讲评对于数学复习的效果来说至关重要,很多教师在试卷讲评时只满足于试卷题目的重复求解,有的教师在试卷讲评时只能做到简单的答案抄写,有的教师对于学生答卷中的问题不能做到精确的统计以至于讲评课的针对性效果缺失. 笔者以为,上述做法显然是不够的,现就自己的教学实践谈谈自身的做法、体会与感受.
[?]全面统计学生的答卷情况
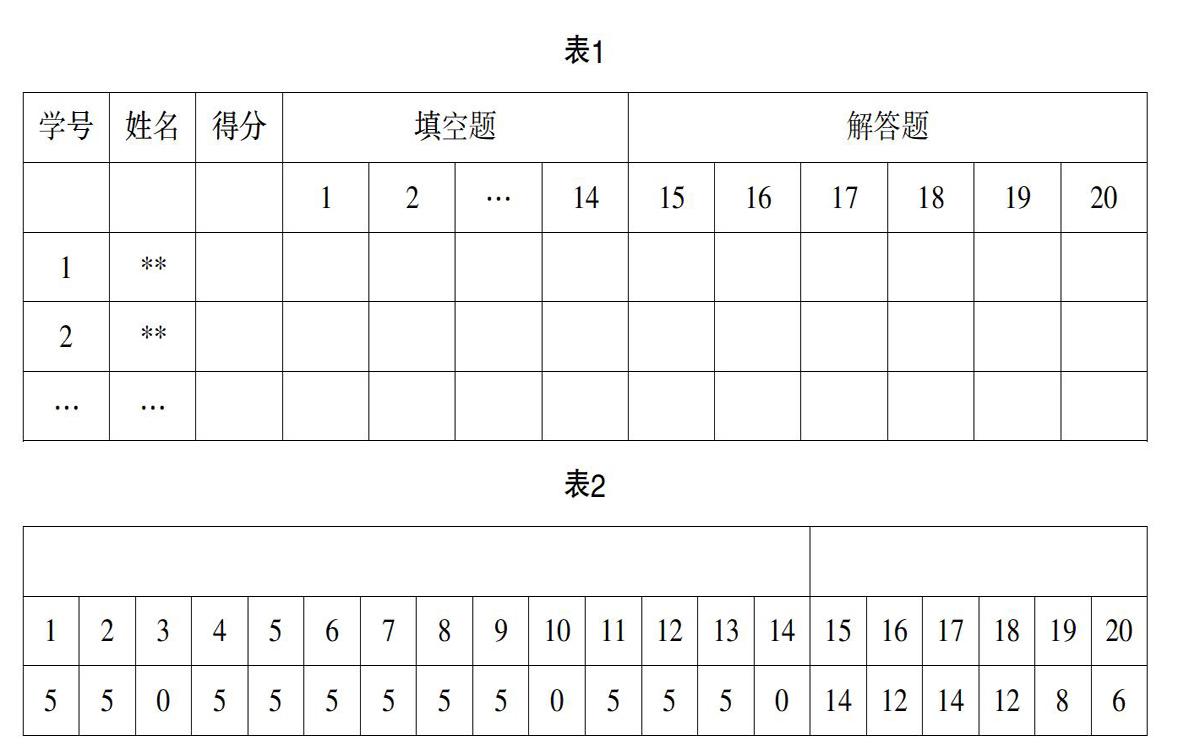
很多教师还保持着将学生考试分数登记在册的传统方式,如此做法对于学生的答卷分析自然是欠缺实效性与针对性的,因此教师对于学生的答卷分析一定要关注各方面的数据,以便后续针对性的讲解. 以下表格是笔者日常的学生答卷登记的形式(表1).
例如,某张试卷上填空题、解答题共计20题,某学生在每道题上的得分情况可以登记如表2.
[?]记录学生的错误情况
仅仅登记学生在各题上的得分是不够的,学生答卷中的错误也应该进行记录和统计. 比如,填空题的解答虽然只能在结果上呈现出来,但学生的不同错误结果却是其存在不同问题的反映,就好比病人发烧需要就医并化验血液来确定发烧原因一样,所以说教师应有效分析试卷的基础上进行针对性的讲解才能起到对症下药的良好效果.
例如,以下考题:图1是某空间几何体的三视图,半圆与矩形组成了其中的主视图和左视图,图中部分尺寸已经标出(单位:cm),则该几何体的体积为____cm3.
正确答案为. 学生在此题的解答中出现的错误结果有4+,π,. 有的教师认为学生的运算能力弱导致了这些错误,但事实上并不仅仅是这一因素. 实际上,得出4+这一错误结果的学生在空间想象上显然是能力不够的,很多学生将半球下面的圆柱想象成了正四棱柱而产生了这一错误结果. 教师在此题的讲评中就应该首先引导学生将两种几何体的三视图画出来,作出图2所示三视图之后引导学生进行比较和区分,使学生的空间想象能力得到锻炼和提高. 获得π这一错误结果的学生一般都是将球的体积公式错记成了πR3,教师可以针对这一错误结果将正确的球的体积公式V=πR3进行比较,帮助学生加深理解和记忆. 获得这一错误结果的学生则是将圆柱的体积公式错记成了2πR2h.
由此可见,学生在此题上的解答错误并不仅仅是运算能力的问题,如果教师简单地将学生的错解原因归结为计算能力这一因素,试卷讲评时又一味地强调计算,试卷讲评必然很难获得良好的效果.
[?]对统计数据进行准确分析
对全班的平均分、最高分、最低分、标准差、各分数段人数进行准确的统计之后要计算的是各题的得分率,只有这样才能对学生各方面存在的问题获得全面的了解,这对于接下来的试卷讲评来说具有导向性的作用.
比如,以下一道高三数学测试题:如图3,在直三棱柱ABC-A1B1C1中,D,E分别为BC边和B1C1边上的点,CD=B1E=AC,∠ACD=60°. 求证:(1)BE∥平面AC1D;(2)平面ADC1⊥平面BCC1B1.
该班共57名学生,在此题上得满分14分的有44人,得12分的有10人,得8分的有3人. 对得12分的学生的答题情况进行分析发现,很多学生解决第(2)问时,由条件CD=B1E=AC,∠ACD=60°,证明AD⊥CD不到位. 对得8分的学生的答题情况进行分析发现,这部分学生除对上述证明不到位之外,在证明BF∥C1D时也不够清晰.
[?]确立讲评目标和主线
试卷讲评课应与其他课型一样制定明确的教学目标,因此,教师可以根据以上情况的统计和分析、测试的用意和目的进行讲评教学目标的制定,在合理讲评目标的引领下作出紧扣重点、突出主题的有效讲评.
一般来讲,一份试卷所包含的20道题目会从知识、技能、方法以及思想等多个角度对学生的数学水平与能力进行测试,应该说,测试是评估学生数学学习情况的一种有效手段. 因此,教师应该根据学生解题中反映出来的问题进行针对性的讲评,使学生在有意义的知识与方法的再梳理中获得更好的理解. 将试卷从头到尾重新讲一遍的讲评教学自然是无法达成这一目标的,如果将一点都不遗漏的详细讲解作为试卷讲评的有效手段,那就无须再对学生的答题情况进行统计和分析了. 任何一份试卷上的题目不可能是每位学生每题都不会做的,考试时未能获得正确答案的题目,在试卷讲评时,或许已经茅塞顿开. 再者,简单的、无一遗漏的重复讲评很有可能对学生形成就题论题的影响,学生不能搞清楚问题本质的同时,也无法应对稍有变化的新题. 因此,教师在试卷讲评课之前就应该对试卷上的题目和内容进行合理的组合,突出主要问题并遵循以下原则进行内容的整理、组合并落实有效的讲评.
1. 知识为主线的双基缺陷讲评
知识点的覆盖率是教师在试卷讲评课上首先要考虑的. 一般来讲,试卷的出题人对于主干知识的检测往往会有多角度的设置,这对于学生是否理解、掌握这些主干知识来讲具有全面性和真实性. 因此,很多学生往往会因为知识缺陷、基本技能生疏等原因在答卷中产生错误. 所以,教师在试卷讲评时应有目的地将一些题目按照知识块组合起来,比如存在问题的函数知识的题目集中在一起讲评,使学生在纠错的过程中对函数部分的知识结构形成更好的理解与掌握,使学生对函数知识的内部联系获得更好的理解.
2. 方法为主线的思维障碍突破
以知识为载体的数学试卷同时也是对学生数学思维能力与思想方法的考查,试卷区分度得以增加的同时也能对不同层次学生的能力形成客观的评价. 或许这些考查学生能力的问题在试卷总题量中的比重并不大,但令学生的思维过程在这些试题中得到充分的展现,能使教师准确获悉其解题中的思维障碍和原因并进行有效讲评方法的选择,使学生在解题讲评中真正获得思维能力的锻炼.
3. 问题为主线的典型错误修正
知识、方法中的漏洞令学生难免产生一些错误,学习习惯也会导致其在不该犯错之处出错. 事实上,有的错误,只要学生在解题后进行仔细的检查就能得到避免,根本无须多讲,但现实情况是,犯下这种错误的学生中仍有下回继续犯类似错误的现象. 比如运算错误,教师在统计分析学生的答卷情况时,可以将这一类的问题整合在一起并令学生自行订正,然后教师再进行算理的阐明与算法的选择,引导学生不要盲目自信于自身的计算能力,使学生逐步形成理性选择、合理运算的良好习惯,并因此在计算上获得较高的正确率.
[?]设计矫正反馈练习
引导学生在试卷讲评后进行总结和分析是每次考试结束之后应有的环节,学生在有效的分析和总结中往往能够找出本次考试的成功与不足之处,纠正现存问题的同时也及时进行查漏补缺. 事实上,在学生纠错、总结的基础之上,还应进行正确方法的强化练习,这是有效帮助学生矫正错误并形成正确技能、提升思维准确性、减少失误的有力措施. 教师在设计反馈练习时应考虑到学生答卷中的错误,将错题中的条件、结论、图形位置等进行一定的變化进行新题的编写. 需要注意的是,片面追求难度或变化太大的反馈练习也是不合适的,教师一定要本着促进学生掌握试题解法与本质的原则进行反馈练习的编写或选择,这种有的放矢的反馈练习必然能令学生的能力有所提高.
