Sn掺杂对In2 O3热电性能的影响

胡 阳， 叶灵云， 闫玉丽

(1. 河南大学物理与电子学院计算材料科学研究所， 开封 475004； 2. 郑州成功财经学院 国际经济与贸易系， 郑州 451200)

Abstract: The effects of Sn doping on thermoelectric transport properties of In2O3were studied using the first-principles method and the semiclassical Boltzmann theory.. The calculations of formation energy show that Inb sites are most likely to be replaced by Sn. It should be noted that the calculated formation energies of the stable conguration are negative for x = 1，which suggests that they are energetically stable at 0 K and may be synthesized under appropriate experimental conditions. However, the calculated formation energies are positive for x= 2 and 3, which indicates that they are thermodynamically unstable at 0 K. Thus in this paper, we only calculate the electronic structure and transport properties of In31SnO48. The calculation of electronic structure shows that Sn doping has little influence on the band structure of In2O3, but the Fermi level position would be moved toward the conduction band. Based on it, we predict that the electronic transport properties of In2O3 by using the semiclassical Boltzmann theory and rigid-band should be almost in agreement with that of In31SnO48. The transport properties change obviously with the chemical potential near the top of the valence band and the bottom of the conduction band. Between the top of the valence band and the bottom of the conduction band，ZeT close to unity and does not change with the temperature and chemical potential. Excitedly, comparison of the electronic transport properties of In2O3 by using the semiclassical Boltzmann theory and rigid-band with that of the experimental results, we find that the result of theoretical calculation is consistent with that of experimental study in the case of the same temperature and chemical potential. And the chemical potential is far above the bottom of the conduction band, which shows that the experimental evaluation of thermoelectric conversion efficiency is expected to be improved at lower doping level.

1 引 言

环境污染和能源危机是当今世界面临的两大问题. 热电材料作为一种新的可再生能源材料受到人们的广泛关注. 热电材料既可以制作热电发电机也可以制作热电致冷器. 在本质上，热电冷却器和发电机都属于热机，与传统的蒸汽发电或热泵循环类似，但它们使用固体载流子作为工作载体，而不是气体或液体[1]. 因此，热电材料做成的装置具有不使用任何移动的机械部件、维护成本低、寿命长[2]、易于控制等优点. 但热电材料做成的器件一直没有得到广泛的应用，其中一个很重要的原因就是现有热电材料的转换效率还比较低. 目前，热电研究的两大重点是发现具有高热电效率的新材料[3-7]，以及热电器件的设计和优化[8-10]. 我们的工作主要集中在通过理论计算寻找具有高热电性能的材料. 材料的热电转换效率用无量纲的ZT值表示：ZT=S2σT/κ其中，S为塞贝克系数，单位是VK-1；σ为电导率，单位是S/cm；T为绝对温度，单位是K；κ叫热导率，主要是由声子散射产生的晶格热导率κ1和载流子运输产生的电子热导率κe两部分，单位是Wcm-1K-1. 高性能热电材料需要同时具备最大化功率因子S2σ和最小的热导率κ. 从20世纪90年代中期开始，各种高效热电材料如铬合物[11]、方钴矿化合物[12]、Zintl相[13]、氧化物[14， 15]和纳米材料[16,17]等被开发. 氧化物热电材料具有耐高温、抗氧化、制备工艺简单、环境友好等特点,被认为是一种高温下潜在的热电材料.

In2O3透明导电薄膜由于高的电导率和良好的透光性，而成为具有优异光电特性的电子材料之一. 特别是铟锡氧化物(ITO)是一种由不同比例的铟、锡和氧组成的三元化合物，它常用于制作透明导电涂料，如液晶显示器、面板显示器、等离子显示器、触摸板和电子墨水等. 近年来，人们开始关注ITO的热电特性. Guilmeau等人，用标准的固态反应方法制备不同掺杂浓度的In2-xMxO3(M=Ti, Zr, Sn, Ta, Nb，从x=0到x=0.2)的样品[18]. 对于Sn掺杂样品，当x=0.06～0.1(3～5 at.%)时，最大载流子浓度n=10.8×1020cm-3，电导率σ=5×103Scm-1，在室温下塞贝克系数为20 V/K，但最大ZT值在1000 K温度下仅为0.28[18]. 另有研究表明，Sn高掺杂浓度的In2O3具有半金属导电性(室温下电导率高达104Ω-1cm-1)[19]. 如此高的导电性引起了我们的研究兴趣，于是我们通过刚性带模拟和Sn元素掺杂In2O3的电子结构和热电特性进行了理论研究. 电子结构的研究表明Sn掺杂对In2O3的能带结构的形状影响不大，于是我们推断刚性带模拟 In2O3和具体元素掺杂的电子输运特性应该比较符合. 通过将刚性带模拟的电子输运特性和相同浓度的Sn掺杂对比，揭示实验上虽然有高的电导率却表现出这么低的热电转换效率的内在原因，为实验上通过掺杂提高In2O3热电转换效率提供了理论指导.

2 计算方法

我们采用基于密度泛函理论(DFT)的VASP程序包[20-22]对In32-xSnxO48(x=0,1, 2, 3)的晶胞结构[23]进行优化. 局域密度近似(LDA)与CeperlyAlder交换相关函数[24]作为Perdew和Zunger杂化参数[25]. 用不同的K点和平面波截断能进行了收敛性测试，最终截断能设置为500 eV，第一布里渊区内的积分K点选为5×5×5，电子自洽相互作用的能量收敛标准定为10-5eV. 通过对原子位置和晶格参数的弛豫计算，得到最稳定的晶格结构. 当作用在每个原子上的Hellmann-Feynman力小于0.02 eV/Å时，力优化结束.

在优化的晶格结构基础上，采用基于密度泛函理论的全势线性缀加平面波的WIEN2k程序包[26-29]，计算了In32-xSnxO48(x=0,1, 2, 3)的电子结构. 用的是(Perdew-Burke-Ernzerhof with Generalized Gradient exchange-correlation potential)PBE-GGA[30]交换关联势. 但由于GGA一般会低估材料的能带带隙，为了得到更加准确的带隙，在PBE-GGA的基础上，我们采用modifed Beck-Johnson[21]TB-mBJ展开带隙. 平面波截断Rmt×Kmax=7，Kmax是k矢量的最大值，muffin半径对O和Sn原子被选为1.95 a.u.，对于In原子被选为1.99 a.u.. 在自洽计算中把第一布里渊区内k点设为1500，当两次迭代的总能量差小于0.0001 Ry时，自洽收敛.

输运性质计算采用的是基于半经典玻尔兹曼理论的BoltzTraP[31,32]. 其中BoltzTraP程序假设弛豫时间和能量无关，为一常数. 在能带结构不变的基础上通过移动费米能级模拟掺杂. 有研究表明这一近似对金属或掺杂的简并半导体是适用的[33-36].

3 结果与讨论

3.1 电子结构

众所周知，一个In2O3原胞有80个原子，其中包括32个In和48个O. In原子占据两个不等价位，分别标记为In b和Ind位. 通过计算各种取代位的形成能，并将各种情况下的形成能对比，发现取代Inb位的In31SnO48的总能比取代Ind位的In31SnO48的总能低了67 meV，说明Inb位比Ind位更容易发生取代，这和Nadaud等人的计算结果一致[37]. 因此，接下来的工作我们只考虑Inb位被取代的情况. 值得注意的是，x=1,2,3时In b被Sn取代的形成能中，只有x=1，即一个Inb位被Sn取代的形成能是负值，此时Sn在In2O3中的原子掺杂浓度是3.12 at. %. 而x=2和3的形成能是正值，考虑到材料的热力学稳定性，本文重点研究一个Inb位被Sn取代的电子结构和热电特性，并和纯的In2O3在刚性带模型下的结果对比. 所以本文我们重点讨论一个Inb位被Sn取代的电子结构和电子输运性质.

纯的In2O3和一个Sn掺杂的In31SnO48的能带结构如图1所示，从图中的结果我们能够看出，In2O3的带隙是3.23 eV，这和Hanberg等人的计算结果[38]非常符合，证明了我们计算结果的可靠性. 导带和价带的极值点CBM和VBM都在Γ点，第二条导带距CBM超过1.5 eV，所以对输运性质几乎没有贡献. 第一条导带能量跨度较大，所以材料的有效质量非常小，只有0.02 m0，所以电子的载流子迁移率较高，但由于导带极值点的态密度较小，所以电子的电导率虽然较大，但塞贝克系数较小. 价带顶的能带较平坦，价带有效质量较大，是3.55 m0，所以空穴电导率较小. 又由于价带极值点附近距离VBM小于kBT的能量范围的N点和P点能态对输运性质的贡献是必须考虑的，所以空穴塞贝克系数较大. 而一个Sn掺杂对In2O3的能带结构几乎没有影响，In31SnO48的带隙为3.18 eV，费米能级进入导带，第一导带和第二导带分开，使In31SnO48呈现半金属特性. 对比In2O3和In31SnO48的能带结构，我们可以推断对In2O3的热电特性采用刚性带模拟的结果和In31SnO48的热电特性对比，当两者取相同化学势时应该具有相同的电子热电特性.

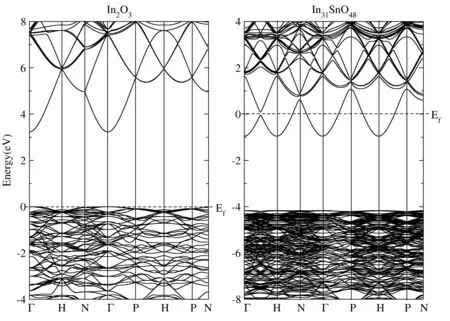
图1 In2O3和In31SnO48的能带结构. Fig. 1 Calculatedband structures of In2O3 and In31SnO48

3.2 输运性质

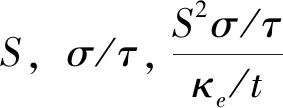
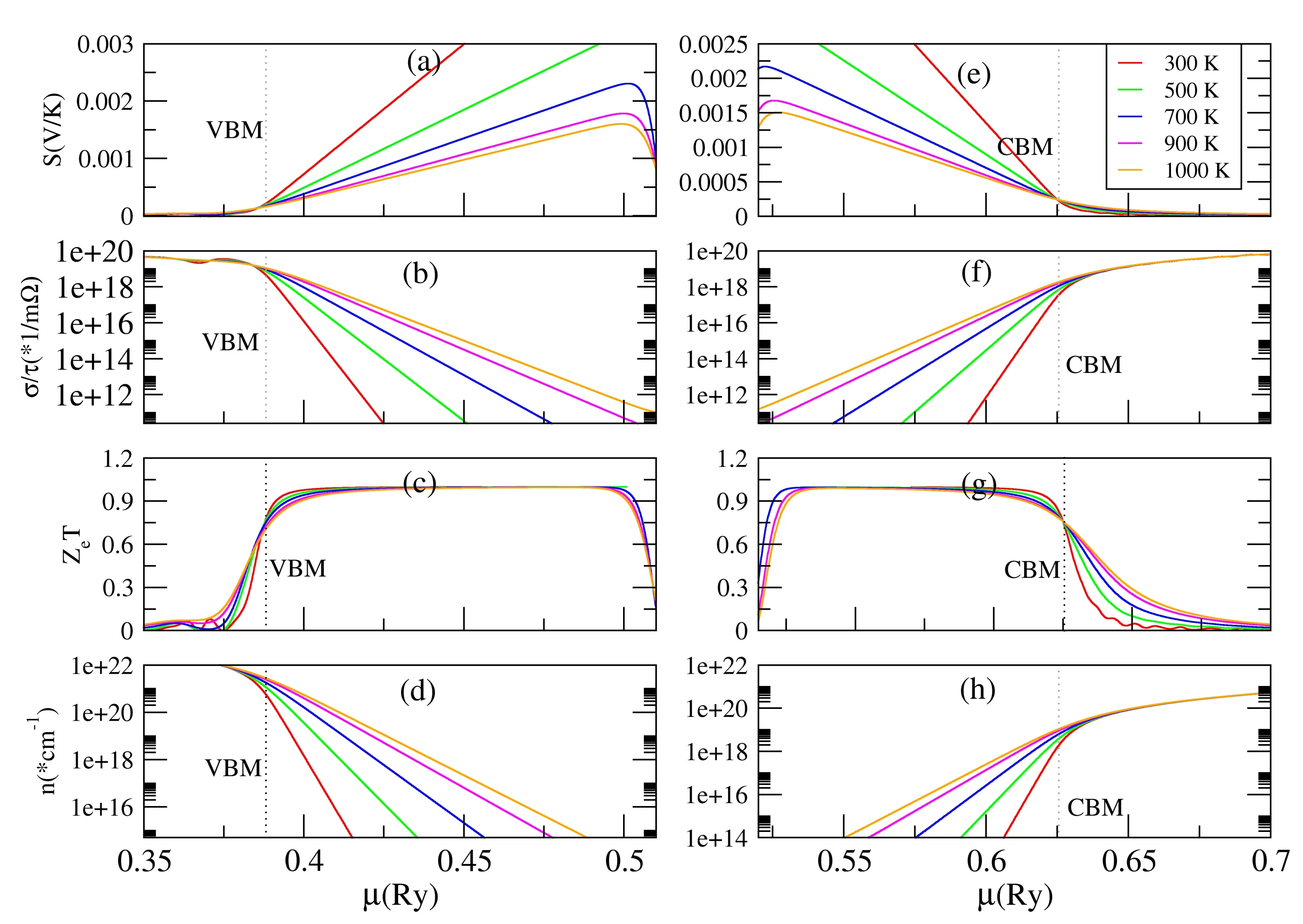
图2 In2O3的电子输运性质随化学势μ的变化. Fig. 2 Transport coefficients ofIn2O3 and as a function of μ.

为了进一步验证上面的推断，即刚性带模拟掺杂In2O3的输运性质和实际掺杂的结果很相近，实验上In2O3的热电转换效率可以进一步提高. 我们将In2O3和In31SnO48在相同化学势下的电子输运性质做了对比. 首先，In31SnO48的费米能级是0.7007 Ry，我们取In31SnO48在化学势为0.7007 Ry附近的电子输运性质随温度的变化，把它表示在图3中(蓝线表示)，然后将In2O3的费米能级采用刚性带模型直接移到0.7007 Ry，将此处的电子输运性质也表示在图3中(红线表示). 从图3可以看出这两种情况下的电子输运性质S，σ/τ和ZeT随温度的变化规律完全一致，只是刚性带模拟的In2O3的ZeT是In31SnO48的近2倍. 且不论导致这两种理论模拟结果差别的原因是什么，但就在相同化学势下两者有相同的变化趋势，证明刚性带模拟In2O3的热电转换效率结果的可靠性.

图3 In2O3(红线)和In31SnO48(蓝线)的输运性质随温度的变化. Fig.3 Transport coefficients of In2O3(red)andIn31SnO48(blue)as a function of the temperature.

为了进一步证明刚性带模拟In2O3的热电转换效率结果的可靠性，我们将刚性带模拟的结果和Guilmeau等人的实验结果对比，具体方法如下：实验中，In2-xSnxO3在1000K时的最大ZT值分别对应样品x=0.002和x=0.006，此时的最大ZT值为0.28，[18]当然这么高的ZT值与现有已成熟材料的热电转换效率还有很大的差距. 在300 K时，x=0.002和x=0.006对应的实验载流子浓度分别是0.58×1020cm-3和1.8×1020cm-3. 将此载流子浓度和图2(h)对比发现，载流子浓度在300 K时对应的化学势分别是0.6512 Ry和0.6532 Ry，从图2(h)发现在这两个化学势下载流子浓度几乎不受温度的影响，这也是为什么实验上两个掺杂浓度不同的样品样品x=0.002和x=0.006的ZT值却是一样的，所以将上述实验中的载流子浓度看成是1000 K时的载流子浓度是完全合理的. 图2 (g)给出在此温度下，两种载流子浓度对应的ZeT分别是0.273和0.249，和实验值0.28非常接近，[18]证明了虽然我们采用的是刚性带模拟且计算热电转换效率时没有考虑晶格热导率的影响，取得的热电转换效率和实验结果却几乎一致. 这可能是由于Sn掺杂对In2O3电子结构影响不大，因此对热电特性的影响也非常小. 另一个原因可能是在温度为1000 K时，材料的晶格热导率非常小，相比于电子热导率几乎可以忽略. 更令人兴奋的是，从图2 (h)可以看出，0.6512 Ry和0.6532 Ry是在导带以上并远离导带，而我们刚性到模拟的热电转换效率取得较大值的化学势范围在导带底以下和价带顶以上的附近区域，所以在更低掺杂浓度下，In32-xSnxO48有望取得更高的热电转换效率.

输运性质的分析表明了采用刚性带模型计算In2O3电子输运性质，发现在价带或导带附近，电子输运性质随化学势的变化非常明显，而在价带以上导带以下的一定化学势范围内，虽然S，σ/τ和n随化学势和温度变化比较大，ZeT化学势和温度几乎没有变化，且n型和p型掺杂下的ZeT非常接近，大小在1附近. 令人兴奋的是，通过将刚性带模型计算In2O3电子输运性质和实验结果对比，发现当温度为1000 K,化学势为0.6512 Ry时的实验ZT=0.28和理论0.273非常接近. 从图2可以看出，化学势0.6512 Ry远在导带底以上，这说明如果选择较低的掺杂浓度，In2O3的输运性质有望进一步提高.

4 结 论

本文通过采用第一性原理并结合半经典玻尔兹曼理论，研究了Sn掺杂In2O3的电子结构和电子输运性质. 发现Sn掺杂对In2O3的能带结构的形状影响很小， 在导带底和价带顶附近，电子和空穴的ZeT在较宽的化学式范围内非常接近并且接近1，这与以往人们宣称的氧化物热电材料的空穴输运性质远大于电子输运性质不符. 由于Sn掺杂对In2O3的能带结构的形状影响很小，于是我们将In31SnO48的的电子输运性质和刚性带模拟In2O3的电子输运性质在相同的化学势下的电子结构对比，发现在这两种情况下的电子输运性质随温度的变化趋势完全相同，虽然两者的电子输运性质的大小有差别，但也证明了刚性带模拟In2O3的电子输运性质的可靠性. 为了进一步证明这个结论，我们将刚性带模拟In2O3的电子输运性质和Guilmeau等人的实验结果对比，发现由于具体掺杂对In2O3热电特性的影响非常小，以及在温度为1000 K时，材料的晶格热导率非常小，相比于电子热导率几乎可以忽略的这两种可能的原因导致理论模拟和实验结果非常符合. 这进一步证明我们理论模拟In2O3热电特性的结果是可靠的，所以如果掺杂浓度选的合适，Sn掺杂In2O3有望在1000 K时取得接近1的ZT值.