计及声子辅助跃迁的单量子点中的非线性法拉第偏转

佘彦超， 张蔚曦， 李 勇， 肖政国

(铜仁学院物理与电子工程系, 铜仁 554300)

1 引 言

法拉第偏转是在光学通讯、数据存储、光学非互易器件(如光学隔离器、光学循环器、相位调制器等)具有广泛应用的一种磁光效应[1-5]. 在块体光学材料中，这一效应非常微弱. 而对于现代光子学或者微纳光子学而言，实现可产生较大的磁致旋光偏转角且能高度集成的法拉第偏转器件或材料成为必须. 近年来, 对磁光特性的研究日益深入, 如超冷原子气，石墨烯超分子材料(graphene metamolecules)，全介质磁光超表面材料(all-dielectric magneto-optical metasurfaces)，半导体量子材料等新的磁光材料不断被发现[6-11]. 基于电磁感应透明效应，Hang等[12]研究了M型五能级冷原子系统中的法拉第偏转. Zhu等[13]研究了在相干驱动的四能级活性拉曼增益介质中的线性和非线性法拉第效应. 这些研究都是基于冷原子系统而展开的, 由于其低温、稀薄等缺陷, 难以在器件微型化设计中广泛应用. 而半导体量子点(SQD)具有类似超冷原子的分立能级结构、较大的电偶极矩、较长的退相干时间, 同时其相干演化可控、易于集成等优势, 在光量子信息通信中具有广泛的应用潜力, 因而引起了研究者的极大关注. 不同于传统光学介质，在SQD系统中，只需要弱光激发能得到如光学孤子，自相位调制效应，交叉相位调制，光学双稳，非线性法拉第偏转等显著的非线性光学效应[14-23]. Hao等[15]在环形四能级的半导体量子点中,通过相位调制抑制线性吸收及双光子吸收的同时实现大的交叉相位调制非线性效应. Yang等[16]研究四能级双激子-激子级联型半导体量子点中基于色散效应与非线性效应相平衡从而形成超慢光孤子对. 块体材料中声子效应非常微弱，通常可以忽略. 但对于微米，甚至纳米尺寸级别的半导体量子材料，声子效应将可能较为显著. Kuehn等[17]在实验中成功地在半导体量子阱中观测到了声子辅助跃迁效应. 因此，本文利用多重尺度方法，研究在外加磁场作用下的声子辅助跃迁效应对环形四能级半导体量子点EIT介质模型中的一束弱的线偏振探测光所发生的法拉第偏转影响. 结果发现，在量子点系统中将可能出现分别是由其中的线性与非线性效应调制两个偏转方向相反的法拉第偏转；且相同的外加磁场作用下，非线性法拉第转角更大. 而通过比较在不同声子辅助跃迁强度下的线性和非线性法拉第偏转曲线的变化可知，随着声子辅助跃迁强度的增加，线性和非线性法拉第偏转角都会逐渐变小，并且非线性法拉第偏转角减小的更多.

2 计及声子辅助跃迁的单量子点系统

本文考虑的是一个由双激子态|3〉、单激子态的两个正交偏振态|i〉(i=1,2)以及基态|0〉所组成四能级半导体单量子点体系[24,25]，如图1(a)所示，图中k表示声子与半导体量子点之间的相互作用强度. 图1(b)则为实验上基于GaAs/AlxGa1-xAs型半导体可能实现的四能级半导体量子点EIT介质模型的实验装置. 在该体系中，弱线性π偏振探测光在与其平行的磁场作用下形成两偏振分量(σ+和σ-). 它们与强控制光分别耦合量子点中的体系中的四组能级跃迁|0〉↔|1〉，|0〉↔|2〉，|1〉↔|3〉和|2〉↔|3〉. 示意图中径向外磁场引起的塞曼分裂Δ=μBMFgFB/ħ[26].

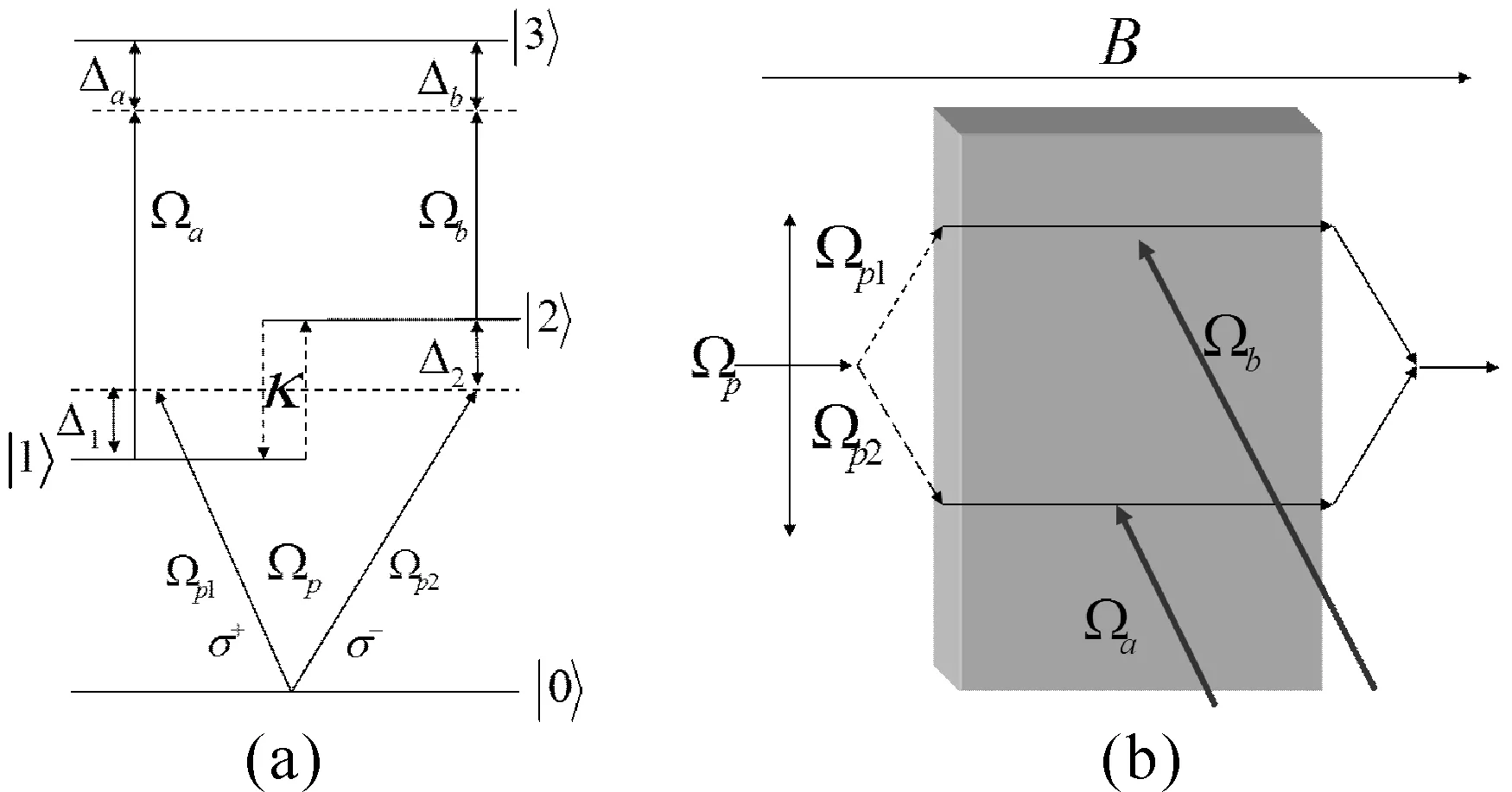
图1 (a)四能级半导体量子点与一弱探测偏振光场和两较强的连续耦合控制光场组成的相互作用系统示意图. (b)四能级半导体量子点EIT介质模型可能实现的实验装置. Fig. 1 (a) Energy-level diagram and excitation scheme of quantum dot system interacting with the strong control field and a weak probe optical field. (b) Possible experimental set-up for the quantum dot device via EIT

相互作用绘景下，利用旋转波近似[27,28]，可得系统的相互作用哈密顿量

(Ωp1|1〉〈0|+Ωp2|2〉〈0|+Ωa|3〉〈1|+

Ωb|3〉〈2|+H.c.)+ik|2〉〈1|+ik|1〉〈2|.

(1)

其中，Ωp1， p2, a, b表示探测光分量与控制光的拉比频率，含k的项即表示声子的辅助跃迁效应.

基于慢变包络近似[27,28]，可以得到半经典理论框架下，描述光场与单量子点相互作用的Maxwell-Schrödinger方程(MS方程)：

(2)

(3)

(4)

(5)

(6)

(7)

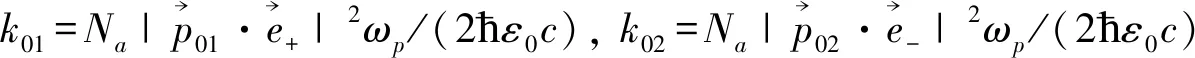
3 探测光的线性传播特性

众所周知，方程(2)不可积，因此利用奇异摄动理论中的多重尺度方法[27,28]来解析地研究四能级半导体量子点EIT系统中探测光脉冲的传播特性.

(8)

(9)

(10)

(11)

(12)

随后，对方程(3)-(12)进行逐级近似求解. 当j=1时，即在线性激发下，系统的探测光场Ωp的Ωp1和Ωp2两个组分所对应的色散关系为

(13)

其中Da=|Ωa|2-(ω+d1)(ω+d3),Db=|Ωb|2-(ω+d2)(ω+d3)，

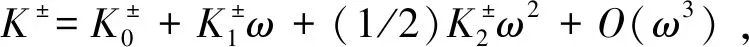
(14)

(15)

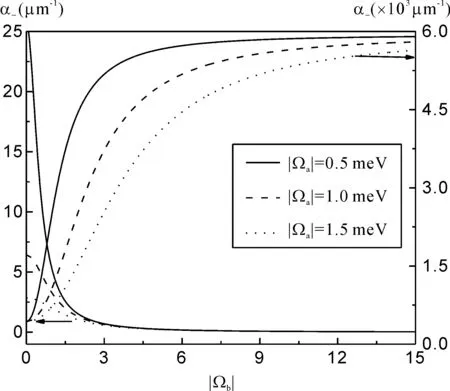
图2 吸收系数α±随连续波控制光拉比频率|Ωb|的变化. Fig. 2 Absorption coefficients α± of the probe field versus Rabi frequency |Ωb| of the control field intensity

为了进一步的直观地获得半导体单量子点EIT系统的线性吸收特性，我们研究了控制光强度及声子辅助跃迁对系统的探测光场Ωp吸收特性的影响. 如图3所示，我们给出了ImK+(ω)来表征探测光场Ωp在不同的控制光光强及声子辅助跃迁强度情况下随着频率ω的变化情况. 图3(a)表示在不考虑声子辅助跃迁的相互作用时，在不同的控制光场强度下，线性吸收随着频率ω的变化情况. 由图3(a)可知，在无控制光场强度时，系统在探测光场的线性吸收曲线会在探测光共振位置出现一个较大的吸收峰；引入控制光后，探测光共振位置处的吸收峰会消失，而在探测光共振位置的两侧则会出现双吸收峰，形成一个单透明窗口，即我们所熟知的电磁诱导透明(EIT)窗口现象；且随着控制光强的增大， EIT窗口也会随之变大. 这主要是因为两个不同的激发通道之间的多光子量子相消干涉所致，即耦合激发通道与反向耦合激发通道之间的相消干涉的结果. 随后数值计算了不同的声子辅助跃迁强度k对探测光场的线性吸收了ImK+(ω)的影响(只考虑|Ωa|=|Ωb|=1.0 meV). 由图3(b)可知，体系的吸收特性曲线的透明窗口随着声子辅助跃迁强度的增加而逐渐变宽，且窗口两侧的两吸收峰高度将会明显的降低. 这是由于单激子态的两个正交偏振态能级在无声子辅助跃迁时间隔很小，而声子辅助跃迁的存在会导致谱线加宽，相对于无声子辅助跃迁的情况，吸收谱线中的吸收峰的宽度也会对应变宽. 图3表明，在不考虑声子的相互作用时，通过调节控制光场的强度可实现对探测光场的EIT窗口及其宽度的调控；当两控制光场的强度相等时，声子辅助跃迁可用于调节电磁诱导透明窗口的宽度，以及吸收峰的幅度和宽度.

图3 在不同控制光强度或声子辅助跃迁强度k下，探测光场的线性吸收Im K+(ω)随频率ω的变化情况. (a)k，(b)|Ωa|=|Ωb|=1.0 meV. 其余参数见文. Fig. 3 Absorption spectra of the probe field versus the frequency ω with the different control filed or the strength of the phonon-assisted transition k:(a) k=0，(b)|Ωa|=|Ωb|=1.0 meV. Other parameters used are shown in the text.

同样，为了进一步的探究半导体单量子点EIT体系的色散特性的影响，我们根据实验选定以下参数c=3.0×1010cm·s-1，k01=k02=3.4×106meV·cm-1，γ1=γ2=0.054 meV，γ3=3.5×10-3γ1，针对不同的控制光场的强度及声子辅助跃迁强度，做出了系统探测光场Ωp的色散特性曲线如图4所示. 图4(a)表示在不考虑声子辅助跃迁的相互作用时，在不同的控制光场强度下，线性色散随着频率ω的变化情况. 当控制光强Ωa=Ωb=0时，探测光场的线性色散曲线在探测光共振位置处的斜率为负值，表现为反常色散，而当控制光强Ωa和Ωb逐渐增强时，相应的线性色散曲线的斜率会由负值变为正值，也就是说相应的线性色散会由反常色散变为正常色散，并且随着控制光强的进一步增大，线性色散曲线的斜率会逐步变小，即群速度随着控制光强度的增大而减大. 而当控制光的强度相等Ωa=Ωb=1.0 meV时，随着声子辅助跃迁强度的变化，体系的色散特性随频率ω的变化情况，如图4(b)所示. 从图中可以看出，随着声子辅助跃迁强度的增大，体系的色散特性总是呈现为正常色散，且探测光在共振位置处曲线的斜率并没有明显的变化. 这说明虑控制光场对体系中的探测光场群速度的调控效应大大显著于声子辅助跃迁效应.

当j=3时，则可得到非线性方程组

(16)

(17)

图4 在不同控制光强度或声子辅助跃迁强度k下，探测光场的线性色散Re K+(ω)随频率ω的变化情况. (a)k=0，(b)|Ωa|=|Ωb|=1.0 meVFig. 4 Linear dispersion Re K+(ω) of the probe field versus the frequency ω with the different control filed or the strength of the phonon-assisted transition k:(a)k=0，(b)|Ωa|=|Ωb|=1.0 meV.

(18)

(19)

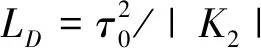
(20)

(21)

其解为u1=exp(-iφ1s),u2=exp(-iφ2s)，其中φ1=g11,φ2=g22为探测光两分量的法拉第偏转角, 它是由非线性效应贡献得到. 将解写为初始场变量的形式Ωp1,p2=U0exp (iK+L-iφ1,2L/LNL)(ω=0),L为半导体量子点EIT介质的长度.

4 探测光的线性与非线性法拉第偏转

为了便于讨论，定义为探测光非线性和线性法拉第偏转角分别为φNL=L[φ1-φ2-(g11-g22)/LNL]/2，φL=L[φ1-φ2]/2.而探测光在半导体量子点EIT介质中的透射率为

(22)

其中参数φL仅取决于系统的线性性质，而φNL则同时取决于系统线性和非线性性质.

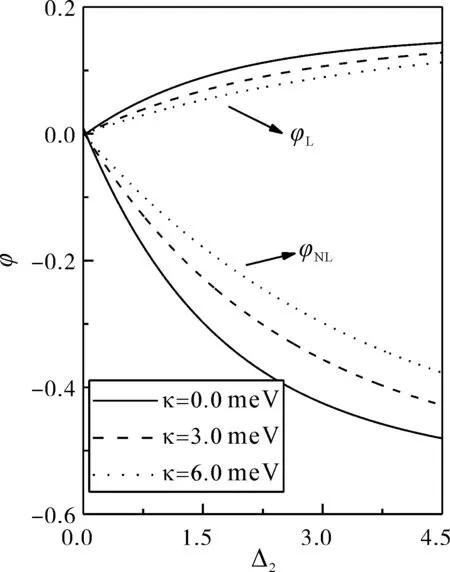
图5 在不同声子辅助跃迁强度k下，线性法拉第偏转角φL和非线性法拉第偏转角φNL随失谐Δ2的变化情况. Fig. 5 The linear and nonlinear Faraday rotation angle versus the strength of the phonon-assisted transitionk

根据目前实验所实现GaAs/AlxGa1-xAs半导体量子点体系的条件, 可选取以下参数：γ1=γ2=0.054 meV，γ3=0.001γ1，Δ1=1.0γ1，Δ3=10.0γ1. 耦合控制光场的拉比频率Ωa=1.003 meV，Ωa=0.997 meV，探测光场的传播系数为k01=k02=3.4×106meV·cm-1半导体量子点EIT介质的长度为L=0.33 μm，非线性长度LNL=0.23 μm. 由于失谐量Δ2=Δ+ωp2-(ω2-ω0)，而塞曼效应位移Δ=2(μB/ħ)gB与磁场B有关，因此，通过调节Δ2来能控制磁场强度B对出射探测光的法拉第偏转的影响. 数值模拟了线性法拉第偏转角和非线性法拉第转角随Δ2的变化曲线. 如图5所示，非线性法拉第偏转角朝着负值方向变化，而线性偏转角朝着正值方向变化，这说明非线性与线性法拉第偏转的方向相反，而且随着失谐量Δ2的增加，线性和非线性法拉第偏转角都是先增大，然后再逐渐保持不变. 此外，对于确定强度的外加磁场，表示非线性法拉第和线性法拉第的曲线偏离直线传播方向即纵轴零值位置的程度也不同，表示非线性法拉第偏转的曲线偏离得更远. 这说明在相同的外加磁场作用下，非线性法拉第转角更大. 而通过比较在不同声子辅助跃迁强度下的线性和非线性法拉第偏转曲线的变化可知，随着声子辅助跃迁强度的增加，线性和非线性法拉第偏转角都会逐渐变小，并且非线性法拉第偏转角减小的更多.

5 结 论

本文在一个四能级半导体单量子点EIT结构中，基于相互作用绘景下的半经典理论，研究了由一束弱线性探测光在与其平行的磁场作用下形成两正交偏振分量，再联合两束强耦合控制光与半导体单量子点相互作用所组成半导体量子点EIT介质中声子辅助跃迁对探测光的线性光学特性的影响和非线性动力学性质. 结果表明，在线性范围，EIT的实现依赖于控制光场的强度和声子辅助跃迁强度的调控. 不考虑声子辅助跃迁的相互作用时，控制光场可改变EIT窗口的宽度及群速度的大小；当控制光场的强度一定时，声子辅助跃迁可用于调节电磁诱导透明窗口的宽度，以及吸收峰的幅度和宽度，但对群速度并没有明显的影响. 此外，我们还研究了如何通过改变外加磁场的强度实现对探测光偏振方向的控制，即数值计算了探测光的线性与非线性法拉第偏转角. 我们发现非线性法拉第转角在相同大小的磁场作用下要大于线性法拉第转角，而且非线性与线性条件下，法拉第偏转的方向相反，而且随着声子辅助跃迁强度的增加，线性和非线性法拉第偏转角都会逐渐变小，并且非线性法拉第偏转角减小的更多. 我们的研究可能对于弱光条件下的光信息处理和传输具有潜在的应用价值.