Al3X(X=Zr、Ti、Ce、Er)化合物的第一性原理研究
2019-09-17钟明君黄福祥阮海光
钟明君, 梁 爽, 黄福祥, 阮海光, 彭 成
(重庆理工大学材料科学与工程学院,重庆 400054)
1 引 言
铝合金由于密度小、比强度和比刚度高、导电及导热性优良,耐腐蚀性能和机械加工性能好、原料来源丰富且易回收等综合性能,如今被广泛应用于航天、汽车、电子电气、生物医学、建筑等领域,并已发展成为继钢铁之后使用最为广泛的有色金属材料[1-3]. 最近的研究表明,通过添加过渡态合金元素Zr[4]、Ti[5]、Ce[6]、Er[4]有助于提高Al合金的力学性能,这对铝合金的进一步开发具有重要意义. 二元相图[7]显示Zr、Ti、Ce、Er在铝中的溶解度非常小,少量添加时能与Al形成Al3X(X=Zr、Ti、Ce、Er)金属间化合物. Al3X析出时能作为非均质晶核,起到促进形核的作用, 而且它们熔点及硬度高,在晶界分布时能有效减少晶界滑移并阻碍晶界扩张,抑制合金晶粒的长大,起到细化铸态合金晶粒,强化铝合金的效果[8]. 然而,目前对于Al3X化合物的热力学性能、电子结构、力学性能还缺乏系统性的理论研究. 因此,本文通过第一性原理方法计算了 Al3X(X=Zr、Ti、Ce、Er)金属间化合物的生成焓、结合能、态密度、弹性常数,分析了它们的热力学性能及力学性能,并通过电子结构对Al3X化合物的结构稳定性及力学性能进行理论解释,为铝合金的发展和设计上提供基础数据.
2 理论与模型
本文采用基于密度泛函理论(Density functional theory,DFT)赝势平面波法的CASTEP(Cambridge sequential total energy package)总能计算软件包[9]对Al3X(X=Zr、Ti、Ce、Er)金属间化合物进行第一性原理计算. 计算时,电子间的关联互换能利用广义梯度近似(Generalized gradient approximation, GGA)中的PBE(Perdew burke ernzerhof)泛函[10]进行处理,离子实与价电子之间的相互作用以倒易空间中的超软赝势[11]进行描述,并通过平面波截断能进行计算精度控制,Al3X(X=Zr、Ti、Ce、Er)截断能分别为270 eV、350 eV、450 eV、370 eV,构建Al3X(X=Zr、Ti、Ce、Er)超软赝势的电子组态为Al 3s2 3p1、Zr 4s2 4p6 4d2 5s2、Ti 3s2 3p6 3d2 4s2、Ce 4f1 5s2 5p6 5d1 6s2、Er 4f12 5s2 5p6 6s2. 采用Monkhorst-Park方式进行K空间取样以降低降低计算量,Al3X(X=Zr、Ti、Ce、Er)的K空间取样分别为6×6×9、7×7×9、4×4×6、5×5×5. 自洽场计算(Self-consistent field,SCF)采用Pulay密度混合法进行电子弛豫,SCF精度为5×10-7eV/atom. 在性能计算之前,先采用拟牛顿法(BroydenFlecher-Goldfarb-Shanno,BFGS)[12]对Al3X(X=Zr、Ti、Ce、Er)金属化合物的晶体结构进行几何优化以求得局域最稳定结构,晶体结构见图 1. 晶体自洽计算过程中的收敛参数如下:总能量的收敛值为 5×10-6eV/atom,每个原子上的力低于 0.01 eV/Å,公差偏移小于 5×10-4Å,每个原子应力偏差小于 0.02 GPa.
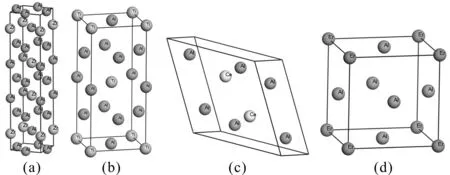
图1 Al3X(X=Zr、Ti、Ce、Er)金属间化合物晶体结构: (a) Al3Zr, (b) Al3Ti, (c) Al3Ce, (d) Al3ErFig. 1 The crystal structures of Al3X(X=Zr, Ti, Ce, Er): (a) Al3Zr, (b) Al3Ti, (c) Al3Ce, (d) Al3Er
3 结果与讨论
3.1 晶体结构及热力学稳定性
晶体的平衡结构是利用第一性原理进行材料性能模拟计算的基础,对计算的精度和可靠性有着显著影响. 因此,本文首先对Al3X(X=Zr、Ti、Ce、Er)金属间化合物的晶体结构进行几何优化,以求得能量最低时所对应的稳定结构,它们的晶体参数如表1所示. 从表1可见,Al3Zr、Al3Ti、Al3Er、Al3Ce金属间化合物的晶格常数与实验值较为一致,计算误差均在可控范围内(2%),表明晶体结构优化过程中所选择的参数是合理的.
为了了解上述金属间化合物的形成难易程度及结构稳定性,本文分别计算了它们的生成焓ΔHf及结合能Ecoh,计算公式如下[17]:
(1)
(2)

化合物的生成焓及结合能的计算结果和相关实验值如表2所示,可以发现本文计算数据和其他文献数据较为接近,说明总能计算过程中参数设置是合理的. 金属间化合物的生成焓ΔHf反映了不同类型原子从单质状态生成化合物所吸收(表现为正能)或释放(表现为负能)的能量,其值越小,化合物越容易形成. Al3Zr、Al3Ti、Al3Er、Al3Ce的生成焓分别为-46.97 kJ/mol、-38.07 kJ/mol、-40.97 kJ/mol、-37.34 kJ/mol,均为负值,表明它们均容易形成. 它们生成焓的绝对值排列顺序为:Al3Zr>Al3Er>Al3Ti>Al3Ce, 则它们的合金化能力也应具有上述规律. 结合能表示孤立原子结合成为化合物所吸收或放出的能量,它能反映出化合物结构稳定性,当其为负值时表明化合物具有稳定结构,且绝对值越大,化合物结构越稳定. 表2所示Al3Zr、Al3Ti、Al3Ce、Al3Er的结合能分别为-489.90 kJ/mol、-465.91kJ/mol、-403.64 kJ/mol、-365.30 kJ/mol,均为负值,表明它们都具有热力学稳定结构. 它们结合能的绝对值排列顺序为:Al3Zr>Al3Ti>Al3Ce>Al3Er,则它们的晶体结构的稳定性也具有上述规律.
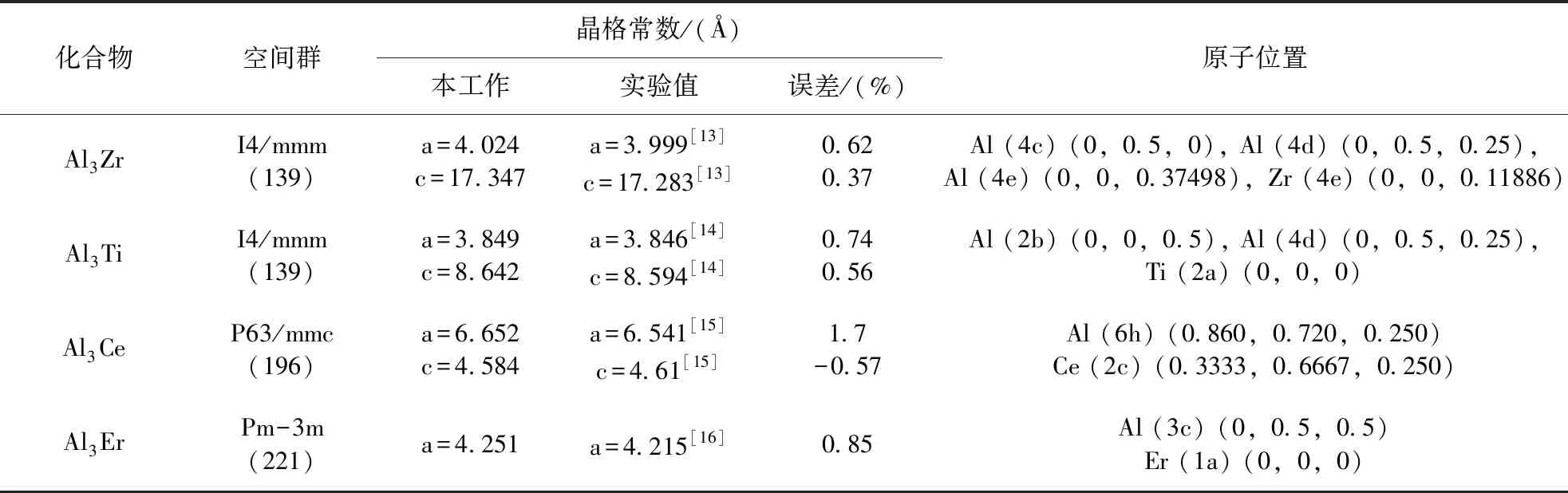
表 1 Al3X(X=Zr、Ti、Ce、Er)的晶体结构参数
表2 Al3X(X=Zr、Ti、Ce、Er)的生成焓及结合能
Table 2 The enthalpies of formation and cohesive energies of Al3X(X=Zr, Ti, Ce, Er)
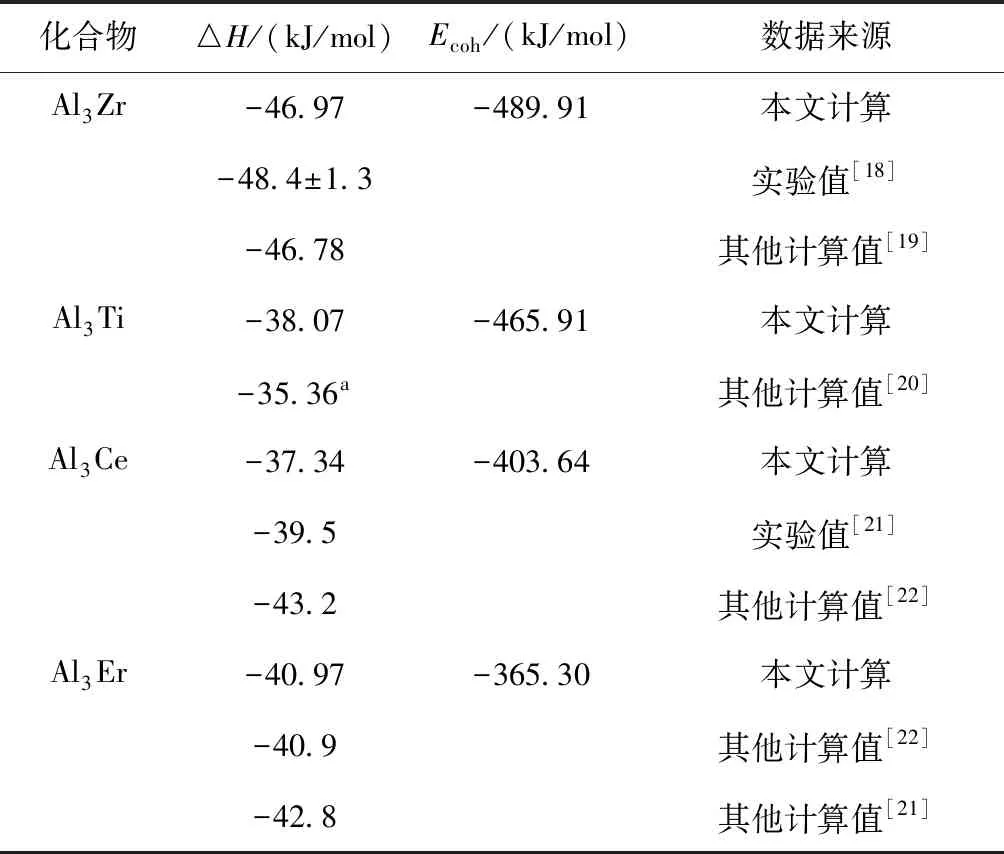
化合物△H/(kJ/mol)Ecoh/(kJ/mol)数据来源Al3Zr-46.97-489.91本文计算-48.4±1.3实验值[18]-46.78其他计算值[19]Al3Ti-38.07-465.91本文计算-35.36a其他计算值[20]Al3Ce-37.34-403.64本文计算-39.5实验值[21]-43.2其他计算值[22]Al3Er-40.97-365.30本文计算-40.9其他计算值[22]-42.8其他计算值[21]
注a为文献[20]中-0.3665 eV/atom换算而来.
3.2 态密度
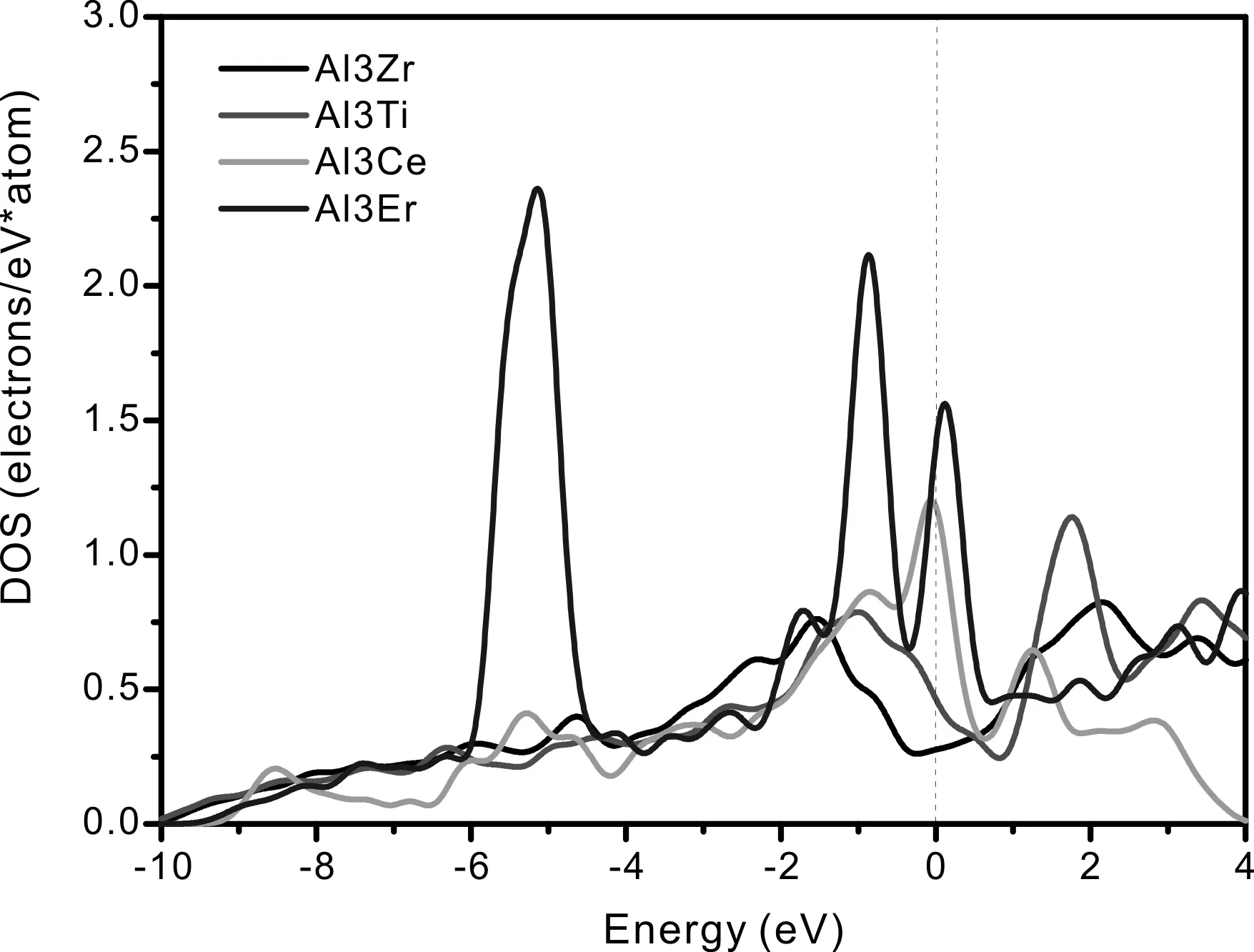
为了分析Al3X(X=Zr、Ti、Ce、Er)化合物的原子间键合方式,并进一步讨论晶体结构的稳定性,本文对它们晶胞(或原胞)的总态密度(Total density of states,TDOS)和分态密度(Points and density of states,PDOS)进行了计算,结果如图2所示. 图中能量0处的虚线为费米能级,由于能量离费米能级较远轨道的电子不参与成键,故而仅考虑费米面附近态密度变化情况,费米面以下为价带,费米面以上为导带.
图2所示的各化合物在费米能级处态密度均不为零,表明它们均具有显著的金属特性. Al3Zr态密度曲线在价带-10-0 eV处,Al-3s、3p和Zr-4d轨道电子重叠较为明显,且在-1.53 eV具有波峰,表明Al-3s、3p和Zr-4d轨道电子具有较强的轨道杂化作用. Al3Ti态密度曲线在价带-10-0 eV处,Al-3s、3p和Ti-3d轨道电子重叠较为明显,且在-1.02 eV左右具有波峰,表明Al-3s、3p和Ti-3d轨道电子具有较强的轨道杂化作用. Al3Ce态密度曲线在价带的-0.84 eV、-0.08 eV处具有较为明显的波峰,主要是Al-3s、3p轨道分别与Ce-5d轨道、Ce-4f轨道具有轨道杂化作用. Al3Er态密度曲线在价带的-5.14 eV、-0.86 eV处具有波峰,且均由Al-3s、3p与Er-4f轨道电子杂化作用. 赝能隙是指费米能级两侧两个波峰对应的能级宽度,直接反映了化合物成键的共价性的强弱,赝能隙越宽说明共价性越强[23]. 图2各化合物总态密度图显示Al3Zr、Al3Ti、Al3Ce、Al3Er化合物的赝能隙分别为3.68 eV、2.80 eV、1.33 eV、0.98 eV,排列顺序如下:Al3Zr>Al3Ti>Al3Ce>Al3Er,它们化合物的共价性强度同样具有以上顺序,这应归因于Al-3s、3p电子分别与Zr-4d,Ti-3d,Ce-5d、4f,Er-4f轨道波形产生共振,成共价键性.
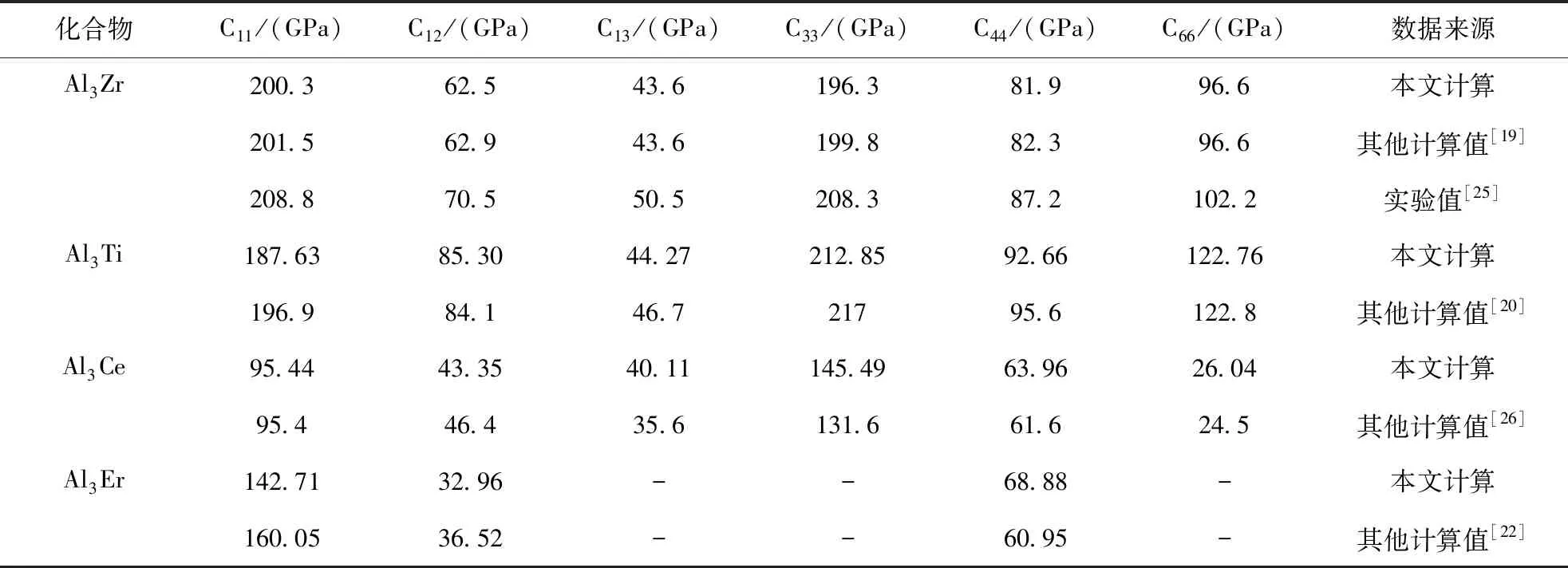
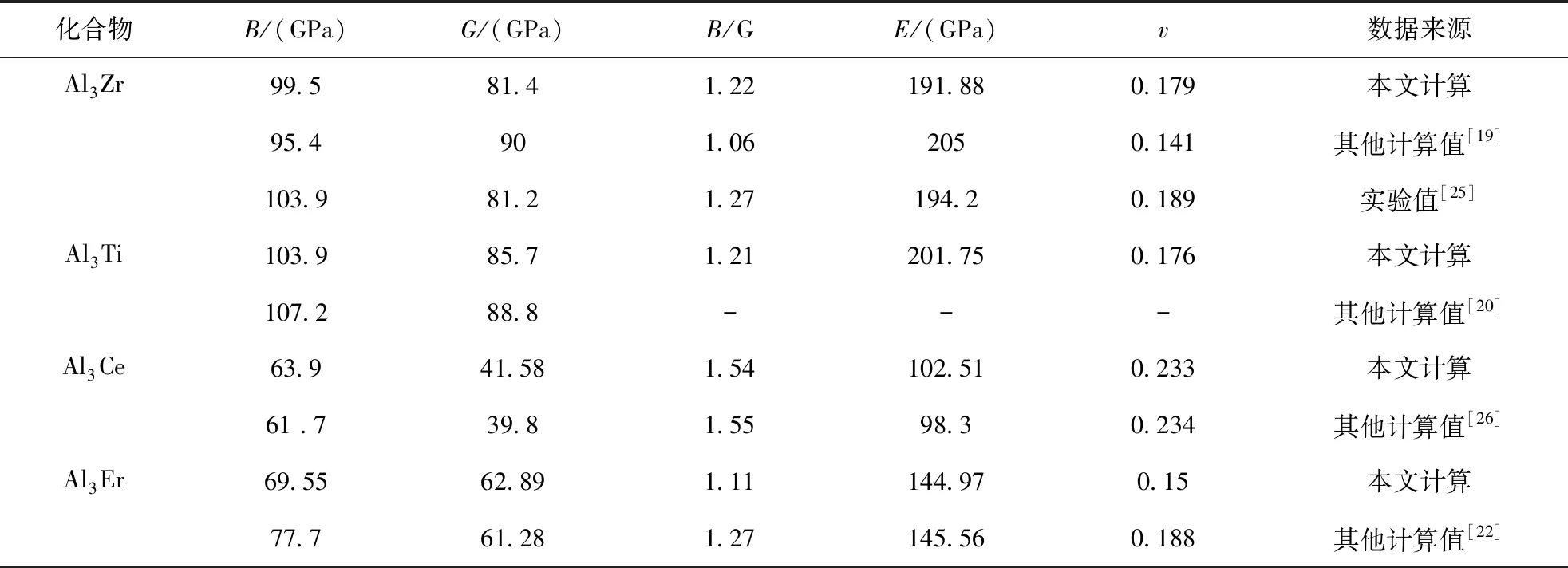
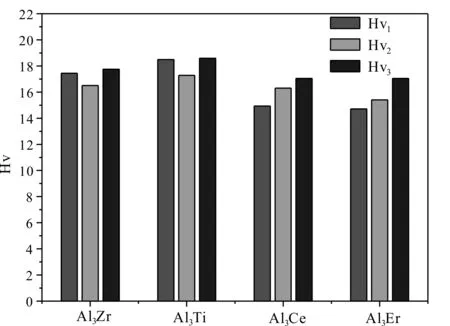
考虑到成分与浓度相同而结构类型不同的晶体,平均每个原子的总态密度费米能级处的电子数可用来评判其价电子结构的活性,即电子数越少,当外界条件发生变化时,晶体电子结构发生改变的几率越小,因而相应的相结构稳定性愈高[24]. 为此选取 Al3Zr、Al3Ti、Al3Ce、Al3Er金属间化合物费米面附近的态密度进行对比,如图3所示. Al3Zr、Al3Ti、Al3Ce、Al3Er化合物平均每个原子在费米能级处的成键电子数分别为0.28、0.47、1.18、1.40 electrons/(ev·atom),它们的大小顺序如下:Al3Zr 图2 Al3X(X=Zr、Ti、Ce、Er)的总态密度(TDOS)及分态密度(PDOS),(a)Al3Zr、(b)Al3Ti、(c)Al3Ce、(d)Al3ErFig. 2 The TDOS and PDOS of Al3X(X=Zr, Ti, Ce, Er), (a)Al3Zr, (b)Al3Ti, (c)Al3Ce, (d)Al3Er 图3 Al3X(X=Zr、Ti、Ce、Er)金属间化合物态密度对比图Fig. 3 The comparison diagram for the DOS of Al3X(X=Zr, Ti, Ce, Er) 材料的力学性能通常与弹性常数有关,根据单晶的弹性常数能进一步计算出多晶体材料的相关弹性性能,如体模量、剪切模量、杨氏模量等,并据此对材料的韧脆性进行判定. 本文中弹性常数的计算是建立在外加一定弹性应变后,通过计算所增加的应变能与弹性应变的导数的基础上,Al3X(X=Zr、Ti、Ce、Er)化合物单晶弹性常数的计算结果如表3所示. 根据Born-Huang的力学稳定性理论,对不同的晶体结构,其稳定性条件是不同的. 正方晶系Al3Zr、Al3Ti具有有6个独立的弹性常数,其保持稳定性条件为[27]: C11>0,C33>0,C44>0,C66>0,C11>C12, C11+C33-2C13> 0, 2C11+C33+ 2C12+ 4C13> 0; (3) 六方晶系Al3Ce同样具有6个独立的弹性常数,其稳定性判据为[23]: C11>0,C11-C12> 0,C44>0, (4) 立方晶体Al3Er由于具有高对称性只有3个独立的弹性常数分别为C11、C12、C44,其稳定性 表3 Al3X(X=Zr、Ti、Ce、Er)化合物的弹性常数 判据为[28]: C11>0,C12>0,C44>0, C11-C12>0,C11+ 2C12> 0; (5) 表3所示的Al3X(X=Zr、Ti、Ce、Er)化合物的弹性常数均满足力学稳定性判据,表明它们都为力学稳定结构. 本文所计算的均为单晶体的弹性常数,而通过Voigt-Reuss-Hill(VRH)近似[29]可以计算多晶的体模量B、剪切模量G,而根据B、G可推算出多晶材料的杨氏模量E,泊松比ν,计算公式如下[23]: (6) (7) 表4为Al3X(X=Zr、 Ti、 Ce、 Er)化合物的弹性性能. 体积模量B表明材料体积抵抗外力的能力,较大的晶胞体积可能会导致更低的体模量,一定程度反映了材料的平均价键强度. 剪切模量G反映了材料抵抗剪切变形的能力,较大的剪切模量通常与较大的C44有关. 杨氏模量E反映了判定材料刚度大小的指标,其值越大表明材料的刚度越大. 比较发现,计算化合物的体模量、剪切模量、杨氏模量均具有如下顺序:Al3Ti>Al3Zr>Al3Er>Al3Ce,表明Al3Ti、Al3Zr抵抗体积变形、剪切变形的能力较强,刚度较大,而Al3Er、Al3Ce抵抗体积变形、剪切变形的能力较低,刚度较小. Pugh[30]认为体模量与剪切模量之比B:G的比值反映看化合物的塑脆性,当B:G值大于1.75时判定为塑性材料,反之为脆性材料,且B:G值越大,材料塑性越好. 泊松比ν是另外一个用于对材料的塑脆性行为进行判定的指标. 当泊松比ν大于0.33时表明化合物为塑性材料,反之为脆性材料. 表4所示的Al3Zr、Al3Ti、Al3Ce、Al3Er的B:G值分别为1.22、1.21、1.04、1.11,均小于1.75,而它们的泊松比ν分别为0.179、0.176、0.135、0.15,B:G值小于1.75,同样泊松比ν小于0.33,可以判定所计算的化合物均为脆性材料,这与Al3Zr、Al3Ti、Al3Ce、Al3Er具有一定共价性,而共价键为方向性键,不利于塑性变形有关,其中Al3Zr、Al3Ti塑性较Al3Ce、Al3Er高. 材料硬度是指材料局部抵抗变形或破坏的一种宏观性能,基于材料微观结构而定量拟合出材料的硬度则一直是材料理论研究者们所关心的方向. 硬度一般分为本征硬度和非本征硬度,本征硬度由材料的键结构、内聚能和晶体结构等决定;非本征硬度即结构硬度,主要取决于材料的显微结构,如缺陷、组织、表面形貌等. 近年来一些研究者提出通过半经验公式来预测材料的本征硬度[31, 32]: Hv3=2(k2G)0.585-3 (8) 这里k为剪切模量与体模量之比G:B. Al3Zr、Al3Ti、Al3Ce、Al3Er的本征维氏硬度如图4所示. 可以发现,尽管不同半经验公式计算得出的Al3Zr、Al3Ti、Al3Ce、Al3Er的本征维氏硬度值存在差异,但是它们具有相同的大小顺序:Al3Ti>Al3Zr>Al3Er>Al3Ce. 因此可以认为Al3Ti具有最 表4 Al3X(X=Zr、Ti、Ce、Er)化合物的弹性性能 大的本征维氏硬度,而Al3Ce具有最小的本征维氏硬度. 不同硬度的中间相对合金的强化效果是不同的,因此不同合金元素的添加对铝合金的强化作用也有所不同. 图4 Al3X(X=Zr、Ti、Ce、Er)化合物的本征维氏硬度Fig. 4 Vickers hardnesses of Al3X(X=Zr, Ti, Ce, Er) 本文通过基于密度泛函理论的CASTEP软件包对Al3X(X=Zr、Ti、Ce、Er)金属间化合物的生成焓、结合能、态密度、力学性能等进行了计算,并得出如下结论: 1. 生成焓,结合能计算结果显示Al3Zr最容易形成,结构稳定性最好. 2. Al3X在费米能级处态密度不为0,表现出金属特性,以此同时,它们还具有一定共价性,且具有如下顺序:Al3Zr>Al3Ti>Al3Ce>Al3Er,这与Al-3s、3p电子分别与Zr-4d,Ti-3d,Ce-5d、4f,Er-4f轨道电子具有较为明显的轨道杂化作用有关. Al3X结构的稳定性受轨道电子在费米能级上的数量影响,而Al3Zr具有最好的结构稳定性应归因于费米能级处的电子数最低. 3. Al3X的弹性常数均满足力学稳定性判据,表明它们的晶体结构都具有力学稳定性. 而它们的弹性模量计算结果表明Al3Ti、Al3Zr抵抗体积变形、剪切变形的能力,刚度较Al3Er、Al3Ce大. 4. Al3X的B:G值与泊松比ν分别小于1.75、0.33,表现为脆性材料,这与Al3Zr、Al3Ti、Al3Ce、Al3Er具有一定共价性,而共价键为方向性键,不利于塑性变形有关. 它们的本征维氏硬度从大到小排列顺序为Al3Ti>Al3Zr>Al3Er>Al3Ce.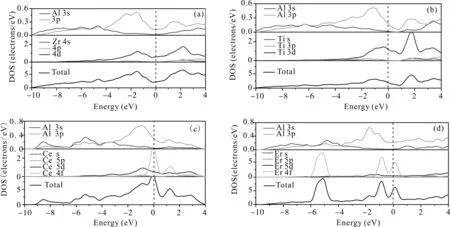
3.3 力学性能
4 结 论
