含有缺陷3C-SiC陶瓷拉伸性能的分子动力学模拟

马小强， 徐喻琼， 苏华山， 杜晓超， 袁显宝， 周建军

( 三峡大学机械与动力学院 水电机械设备设计与维护湖北省重点实验室， 宜昌 443002)

1 引 言

随着核能发展，新一代核能系统对反应堆用材料提出了更高要求，比如，要有较好的抗辐照性能、抗蠕变以及耐腐蚀等. 碳化硅(SiC)具有耐高温、常规化学惰性、低密度、低热膨胀系数以及中子俘获截面小等优良性能[1]，是新一代核能和反应堆结构材料的重要候选材料之一[2]. SiC是以共价键为主的化合物，因缺少能促使晶体变形的滑移系统而呈现出明显的脆性. SiC纤维增韧SiC基复合材料(SiCf/SiC)克服了陶瓷材料的脆性[3]，保持了高温强度、抗蠕变性能、耐腐蚀等优点，作为燃料包壳材料或反应堆内构件材料，在轻水反应堆[4]、高温气冷堆[5]、聚变堆[6]等有良好的应用前景.

在反应堆环境中，由于中子、裂变碎片等对SiCf/SiC复合材料辐照会产生缺陷，致使材料中出现微空洞、元素偏析、位错、非晶等微观结构变化[7-10]. 另外，由于材料制备工艺的限制，在制备SiC材料时不可避免地会在材料中产生空位、微空洞以及非化学计量比等缺陷[11]. 所有这些缺陷都可能使材料的力学性能改变而影响材料的正常使用，甚至可能导致发生事故[12].

SiCf/SiC是由SiC纤维和SiC陶瓷晶体经过材料复合技术制备的具有优越性能的复合材料. SiC晶体是由四个碳原子和一个硅原子(SiC4，硅原子位于正四面体中心，四个碳原子分别位于正四面体的四个顶点)或者四个硅原子和一个碳原子(CSi4，C原子位于正四面体中心，四个硅原子分别位于正四面体的四个顶点)交替以sp3键结合成的正四面体结构. 在不同物理、化学环境下，SiC形成的晶型不同，除了具有立方结构的β-SiC(即3C-SiC)，其他的为α-SiC. 3C-SiC晶体由周期为3层的SiC正四面体结构密排堆积而成的立方晶体结构[12]，只有3C-SiC能够满足核能需要[2].

分子动力学模拟是研究材料力学性能的重要手段的重要手段[13, 14]，对于3C-SiC力学性能的分子动力学研究已经有些成果[15-17]，这些成果主要研究的是无缺陷的单晶体体系、孪晶纳米线和薄膜，而对一定缺陷(空位、微空洞以及反位替代)的晶体拉伸性能研究鲜有报道.

本文应用分子动力学程序LAMMPS[18]对含有空位、微空洞、以及反位替代三种不同缺陷体系的3C-SiC的拉伸性能进行了分子动力学模拟. 通过模拟计算，得到了体系能量和晶体晶格常数以及应力-应变曲线随缺陷“浓度”的变化关系. 通过分析应力-应变曲线，得到了不同缺陷体系的杨氏模量、断裂应变、拉伸强度随缺陷“浓度”的变化关系，最后分析了3C-SiC拉伸断裂机理. 数据分析过程中应用分子可视化软件Atomeye[19]和Ovito[20]直观的观察了拉伸过程中3C-SiC结构的变化情况.

2 计算模型与方法

3C-SiC原子间相互作用使用Tersoff势函数描述[21]，该势函数已成功应用于3C-SiC纳米线的单轴压缩和拉伸等[22]的力学性能模拟，Tersoff势函数具体讨论见第2节.

以晶胞的[100]、[010]、[001]方向为模拟体系的x，y，z坐标轴方向建立10a×10a×10a(a=0.4318 nm，为晶格常数)的3C-SiC单晶模型，该模型包含8000个原子，结构如图1所示. 为了模拟不同的缺陷，分别在无缺陷的单晶模型中随机的删除不同个数的原子形成不同“浓度”的空位型缺陷，或者在无缺陷晶体中删除含有8个原子的团簇，产生不同数量的微空洞. 由于制备工艺和方法的限制，制备的3C-SiC晶体和纤维的碳硅原子的比例不是严格的1:1，碳的所占比例大于硅[1]，因此，本工作以不同比例碳原子随机的取代硅原子位置，形成反位替代缺陷. 三种不同的缺陷类型以及缺陷的“浓度”列于表1.

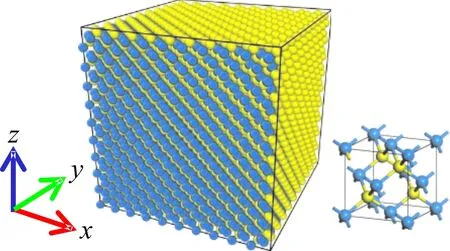
图 1 3C-SiC晶体结构的3D模型，蓝色表示Si原子，黄色表示C原子Fig. 1 The 3D model of 3C-SiC, The blue balls and yellow balls denote the Si and C atoms, respectively

在拉伸模拟之前，对三种不同类型缺陷的所有模拟体系在NPT系综下进行1 ns的弛豫(弛豫时间步长为1 fs)，使体系温度达到300 K并形成稳定结构. 以时间步长为0.1 fs，拉伸应变率为10-4/ps进行拉伸模拟，拉伸时每100个积分步对原子速度重新调节以 控制系统温度不变，而后再次加载应力拉伸. 每一次加载在x轴([100]方向)方向的应力会使体系在x轴方向产生一个微小的应变ε，该应变使模拟体系的x轴方向大小变为1+ε，在拉伸变形的同时体系中的原子重新匹配盒子大小. 拉伸过程中计算每个原子应力的x分量，体系的拉伸应力是对模拟体系中所有原子应力的x分量的平均值.

表1 不同缺陷体系参数

3 原子间势函数

SiC原子间相互作用不仅取决于原子之间的距离，还和原子键的方向有关. Tersoff多体势能够很好地描述SiC体系中的C-Si、C-C、Si-Si间的相互作用关系. Tersoff势描述的系统势能为任意两个原子之间的势能总和：

(1)

其中Vij(rij)是由吸引势和排斥势构成的第i个原子和第j个原子之间的相互作用势能：

Vij(rij)=fc(rij)[fR(rij)+bijfA(rij)]

(2)

其中，rij为第i个原子和第j个原子之间的距离；bij描述了除第j个原子之外所有原子对第i个原子的作用；fc(rij)为原子间相互作用的细化截断函数，与截止半径有关；fR(rij)是第i个原子和第j个原子之间的吸引对势，其主要是指两体相互作用；fA(rij)第i个原子和第j个原子之间的排斥对势，其主要是指三体相互作用. 各个函数的具体形式表示为：

fR(rij)=-Ae-λijrij

(3)

fA(rij)=Be-μijrij

(4)

(5)

式中，A和B为吸引对势和排斥对势的结合能；R为截断半径；R为fC(rij)的参数；λij和μij为吸引对势与排斥对势的势能曲线梯度系数.

上述各量的具体表达式为：

(6)

(7)

(8)

式中θijk为键ij和键ik之间的键角；β为键角系数；ζij为角势能；c,d,h1为弹性常数. 文中所用的参数的取值列于表2.

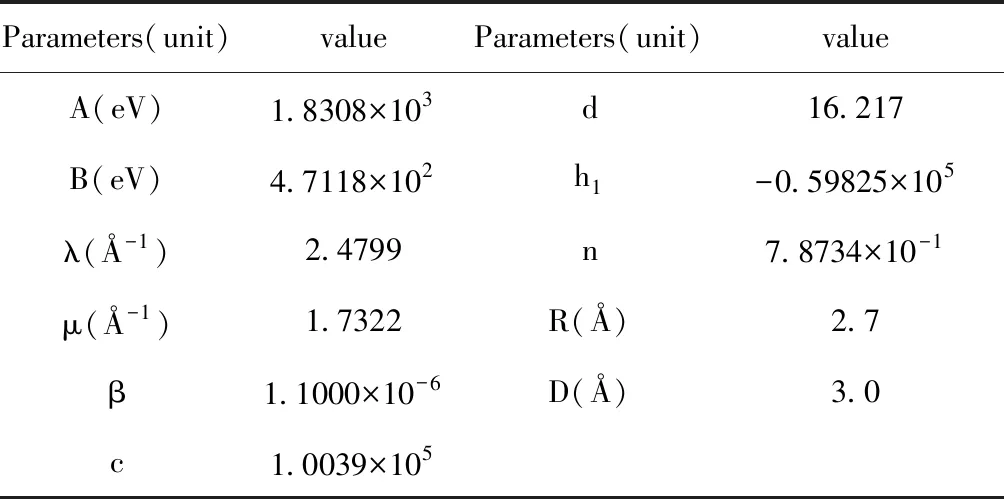
表2 Tersoff势函数参数

4 结果与讨论

4.1 体系能量和晶格常数

拉伸模拟之前，对构建的不同“浓度”的缺陷体系在NPT系综下弛豫1 ns，使体系的温度达到300 K并使结构稳定. 对含有不同缺陷类型的稳定结构的势能和晶格常数计算，计算结果如图2(a)和图3所示. 从图2(a)可以看出，缺陷类型为空位和微空洞时，体系势能随着缺陷“浓度”增大而呈线性增加，反位替代型缺陷的体系势能和没有缺陷的体系势能基本一致，没有发生明显的变化. 分析空位缺陷和微空洞缺陷的体系中原子间的成键情况可以发现，在相同缺陷“浓度”时，空位型缺陷体系中没有完全成键的原子数要比微空洞体系的多，相同缺陷“浓度”时，空位缺陷体系势能要高于的微空洞缺陷体系的势能，相应地，随着缺陷“浓度”增加，空位缺陷体系的势能增加要更快一些. 相同缺陷“浓度”时反位替代缺陷的能量低于其他两种类型，这说明反位替代型缺陷相对要稳定一些.

图 2 体系能量曲线 (a)稳定结构的原子势能曲线； (b)体系能量随应变变化曲线(8%缺陷“浓度”为例)Fig. 2 energy Curve. (a) atomic potential energy with defect concentration； (b) total energy of system as a function of strain

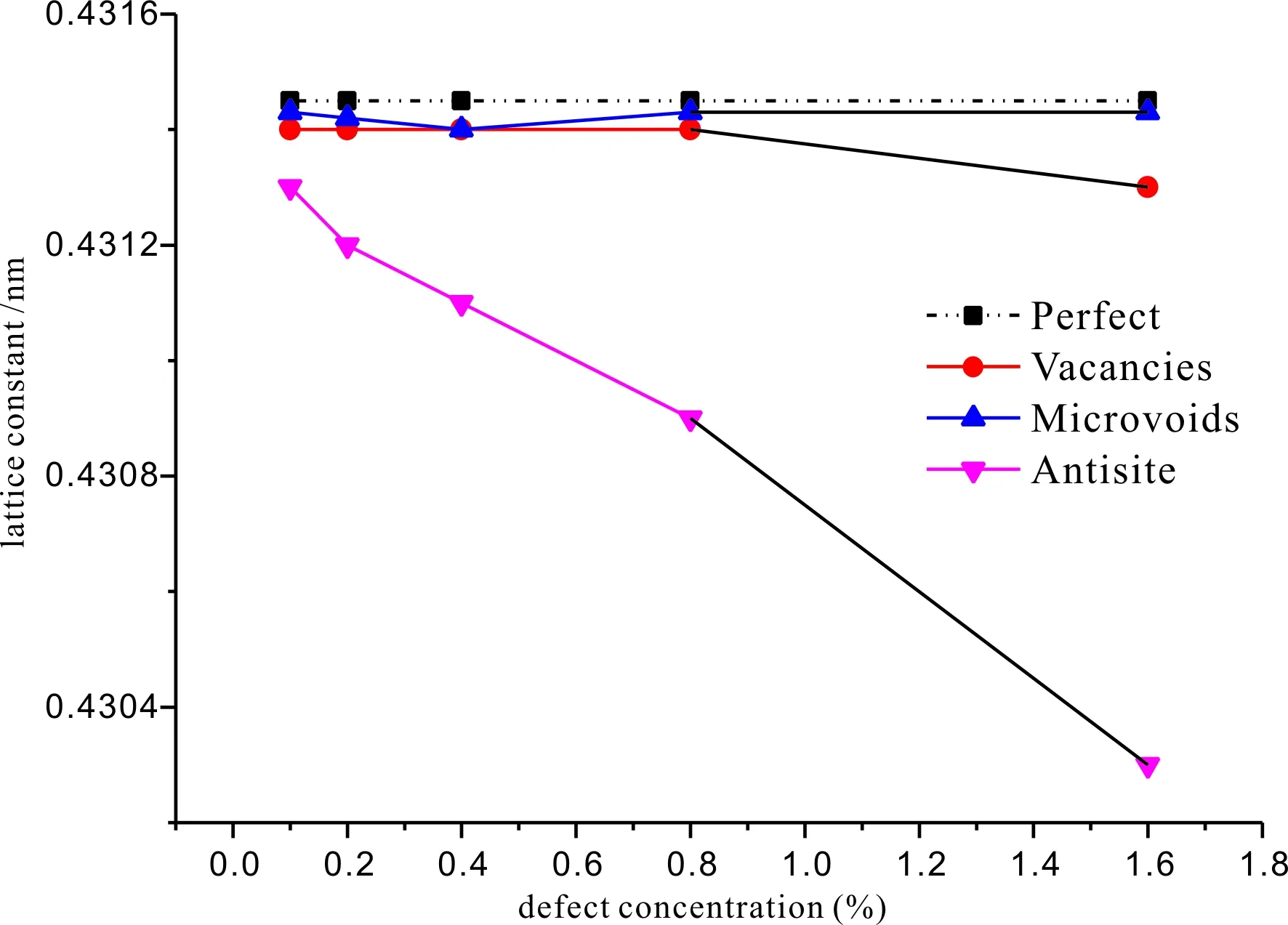
图 3 晶格常数随缺陷“浓度”的变化Fig. 3 Lattice constant with defect concentration

从图3可以看出，缺陷类型不同，晶格常数随缺陷类型变化不同. 和没有缺陷的晶格常数相比，微空洞体系的晶格常数变化不明显，空位体系的晶格常数随着缺陷“浓度”的增加略微减小(缺陷“浓度”为1.6%时减小了0.5%). 反位替代缺陷弛豫后形成稳定结构晶格常数随着被替代原子数增加而减小，发生了较大的变化，在这种缺陷中，当SiC中部分Si原子被C原子替代后，晶体中的部分Si-C键也相应地被替换为C-C键，由于Si-C键(键长为0.189 nm)变成C-C键(键长为0.137 nm)[23]，键长相应减小，晶格常数也变小.

拉伸过程中，外力要对体系做功而使体系的能量发生变化，如图2(b)所示为没有缺陷的体系和缺陷“浓度”为8%时体系总能量(所有原子动能和势能的和)随应变变化关系. 由于模拟过程中保持温度(300 K)不变，所以体系所有原子的总动能不变，体系总能量的变化是由原子之间的势能变化引起的. 从图中可以看出，体系总能量随着应变的增加分为三个阶段. 第一阶段，应变较小时(ε<0.07)原子势能较低，此阶段晶体形变属于弹性阶段，体系能量随着应变增加而缓慢升高，这个过程中系统的能量增加是由于原子之间的键长发生了变化引起的. 第二阶段(应变ε>0.07到体系势能最大)，这个阶段体系能量随着应变增加呈线性增加，对此阶段的原子构型分析可以发现，该阶段晶体体系中原子之间不只是键长发生变化，键角和键结构也会相应发生变化(图7)，从图7还可以看出随着应变增加部分原子键断裂，相应的使体系能量进一步增加而形成不稳定结构. 第三阶段，体系能量突然减小阶段，这个突变是由于晶体发生脆性断裂，大量原子之间失去相互作用，局部应力卸载而释放能量产生的. 由于已经发生了断裂，即使在此阶段卸载应力，体系不可能再恢复到初始状态.

4.2 应力-应变曲线

应力—应变曲线反应了材料的基本力学性能，图4是三种不同缺陷体系(a为空位缺陷，b为微空洞缺陷，c为反位替代缺陷)沿x方向拉伸的应力-应变曲线. 从该组曲线可以看出不同类型缺陷的应力-应变具有相同的变化趋势，尤其是SiC在拉伸过程中会出现的脆性断裂. 体系应变较小时，应力-应变曲线满足胡克定律，随着应变增加，三种缺陷体系都存在应力最大值，这个最大应力就是 拉伸强度，应变进一步增加应力会急剧减小，体系发生脆性断裂，对应的应变为断裂应变.

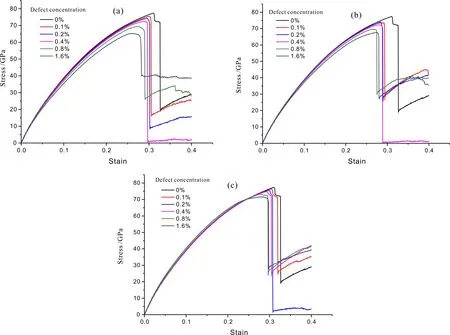
图 4 应力-应变曲线(a)空位缺陷体系； (b)微空洞缺陷体系；(c)反位替代缺陷体系 Fig. 4 Stress-strain curves for (a) vacancies； (b) micro-voids and； (c) antisite with defect concentration

杨氏模量是表征固体材料抵抗形变能力的物理量，取决于材料本身的性质，其值为应变ε<0.03是应力-应变曲线的斜率[15]，对模拟得到的应力-应变曲线中应变小于0.03的部分拟合求斜率，即可得到不同缺陷体系的杨氏模量. 例如，没有缺陷的晶体材料，应力随着应变可以增加到77.4 GPa(拉伸强度)后突然减小，此时应变为0.311(断裂应变). 拟合应变-应力曲线，得到没有缺陷的3C-SiC模拟体系的杨氏模量为485.9 GPa，而温度为300 K时实验值为392-694 GPa[24]，计算结果和实验符合的很好.

4.3 力学性能参数

4.3.1杨氏模量

图5(a)为不同缺陷体系的杨氏模量随缺陷“浓度”变化的关系曲线. 从变化曲线可以看出，空位、和微空洞体系的杨氏模量和反位替代体系的杨氏模量随缺陷“浓度”变化是不同的，前两种情况的杨氏模量随着缺陷“浓度”增加而呈现线性关系减小，缺陷“浓度”为1.6%时的杨氏模量分别减小了6.58%和5.35%，分析拉伸过程的体系原子构型不难发现，空位和微空洞缺陷体系中有部分原子并没有形成四个化学键而成为稳定的正四面体结构，这些没有完全成键的原子不但使体系稳定性变差(体系势能较高)，而且影响了材料的力学性能. 反位替代缺陷的杨氏模量随替代“浓度”增大呈现线性增加，缺陷“浓度”为1.6%的杨氏模量和没有缺陷体系比较增加了7.1%，通过分析反位替代体系原子间成键情况可以发现，杨氏模量增大是因为当碳原子替代硅原子数增加时Si-C键数量减少，C-C键数量增加，在形变较小时C-C 的sp3键的强度Si-C 的sp3键强度大的缘故，因此随着反位替“浓度”的增加杨氏模量也相应地增加.

4.3.2拉伸强度和断裂应变

图5(b)为不同缺陷体系的拉伸强度随缺陷“浓度”变化的关系曲线，图5(c)对应的断裂应变. 从变化曲线可以看出，具有各种缺陷体系的拉伸强度随着缺陷“浓度”增加而减小，并且减小速率有变慢. 对于空位和微空洞缺陷，在缺陷“浓度”小于0.8%时，这两种缺陷的拉伸强度基本相同，缺陷“浓度”大于0.8%时，空位体系的拉伸强度比微 空洞体系的拉伸强度小，随缺陷“浓度”的增加，这个差值变大，这是由于空位缺陷和微空洞缺陷相比，不完全成键的原子数量较多，在外力作用下，这些不完全成键原子更容易移动，拉伸强度要降低的更快一些. 对于反位替代缺陷体系，当应变增加到0.1时，C-C 的sp3键变为C-C 的sp2弱键，随着应变进一步增加C-C的sp2键处会形成空洞，以至于断裂[13]，所以当反位替代原子“浓度”增加时，拉伸强度相应减小，并且减小的更快.

图5 杨氏模量(a)，拉伸强度(b)和断裂应变(c)随缺陷“浓度”的变化曲线Fig. 5 Young’s modulus (a) ，tensile strength(b)and(c)elongation percentage with defect concentration

4.4 断裂机理

图6为拉伸过程中包含182个原子的局部体系图像，图中红色箭头表示此位置原子之间没有成键. 从图6中可以看出在应变小于0.075时，大部分键只是拉伸，没有出现断裂的情况，此过程弹性变形过程，只改变原子间键长，如果此阶段卸载外力，结构还可以恢复到完美的稳定结构. 随着应变进一步增加(但小于0.25时)，原子间所成的键有拉伸变形外，有部分原子键已经断裂，但有部分结构还是晶体结构，此过程是一个塑性变形过程，体系不完全成键原子数增多，甚至在局部出现空洞，这时如果卸载外力，结构已经不能回到没有缺陷的完美状态. 当应变超过断裂应变式，发生脆性断裂. 在室温的纳米压痕实验中也观察到了与上述过程相一致的结果[25]，在一次加载—卸载实验中，即在发生脆性断裂以前，卸载曲线和加载曲线能够完全重合.

单晶拉伸是基于剪切应力在一个滑移面的一种变形机制，3C-SiC是金刚石结构，滑移面为{111},模拟时的加载方向为[100]，在(010)面上的剪切应力不为零，所以，断裂面不是完全的{111}方向，而是和{111}方向之间有一定夹角. 图7是没有缺陷体系脆性断裂前后(ε=0.25为断裂前，ε=0.31断裂应变，ε=0.33为断裂后)体系构型变化，从图7可以看出断裂面的方向不是严格的{1 1 1}.

5 结 论

本文采用LAMMPS程序对含有空位、微空洞和反位替代三种缺陷体系的3C-SiC中沿[100]方向的拉伸变形过程进行了分子动力学模拟，通过对拉伸过程中体系能量、应力-应变曲线、杨氏模量、拉伸强度以及断裂机制的分析，得到了以下有用的结论：

(1)不同缺陷体系稳定结构的能量随缺陷“浓度”增加变化趋势不同，空位和微空洞体系的势能随缺陷“浓度”增加成线性增大；反位替代缺陷的体系能量和无缺陷体系能量基本相同，随替代“浓度”基本没有发生变化. 在拉伸过程中模拟的所有体系的势能变化都经历了缓慢增大，近线性增大和突然减小的三个阶段.

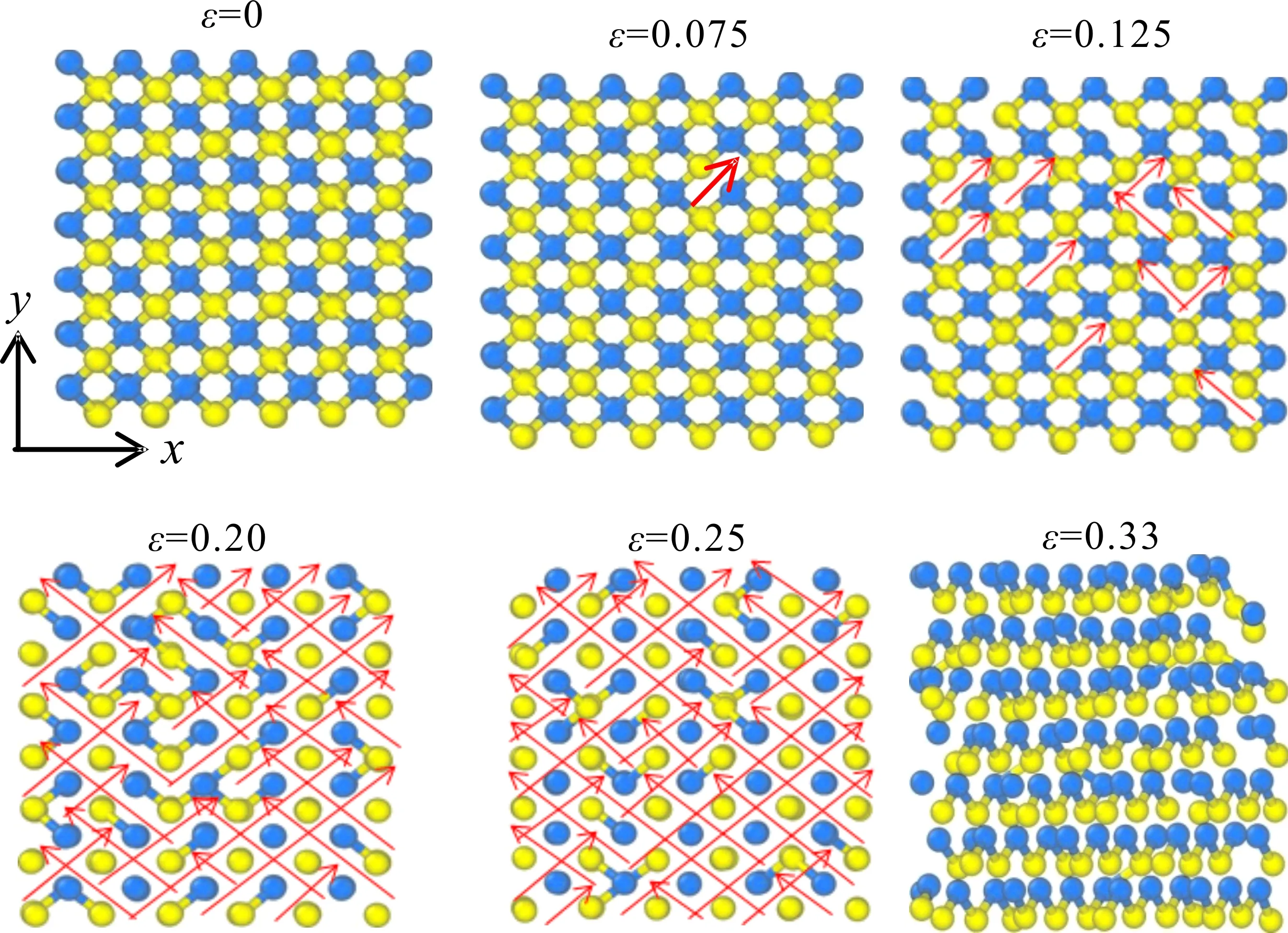
图 6 拉伸过程中原子构形(包含182个原子)Fig. 6 Atomic configurations of 182 atoms of the bulk 3C-SiC with the tensile

图 7 脆性断裂前后原子构型Fig. 7 Atomic configurations before and after brittle fracture for 3C-SiC

(2) 空位和微空洞缺陷体系的杨氏模量随着缺陷“浓度”增加呈线性减小，反位替代缺陷体系的杨氏模量随缺陷“浓度”增加呈线性增加.

(3) 三种缺陷体系的拉伸强度和断裂应变都是随着缺陷“浓度”增加而减小，空位和微空洞缺陷体系减小的更快一些.

(4)单轴拉伸断裂面不是严格的在{111}滑移面.