一维抛物方程界面问题的紧致有限体积格式

于 倩 杨 青

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

有限体积法[1]又称控制体积方法,它是从方程组的积分形式出发,对积分形式进行离散,得到有限体积格式,该方法构造的离散格式简单,满足局部守恒.近年来广泛应用于空气动力学.紧致有限体积法[2,3]是将紧致差分[4]的思想与有限体积法结合所得到的一种高精度算法,已被用于多种类型的方程[5-7].

下边我们考虑如下形式的一维抛物界面问题

(1)

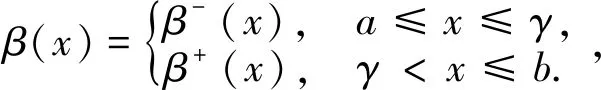
(2)

(3)

本节针对问题(1)-(3)建立紧致有限体积格式.

2 紧致有限体积格式的建立

下面根据界点γ的位置对Ih进行调整. 如果存在xi, 使得xi=γ, 则Ih不变.如果γ∈(xi-1,xi), 当|γ-xi-1|>|γ-xi|时, 我们记xi=γ, 否则xi-1=γ; 也就是说通过节点转移的方法, 使界点成为网格中的一个节点. 为了叙述方便, 记xk=γ,h1=xk-xk-1,h2=xk+1-xk.

其次, 我们对于网格Ih进行对偶剖分,xi-1/2=(xi+xi-1)/2,i=1,2,…,N. 对偶剖分单元记为

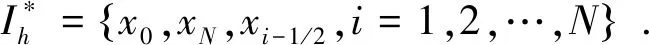
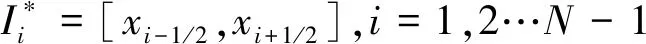
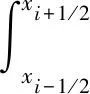
(4)

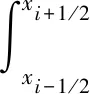
下面我们对T1,T2,T3进行离散,分四种情况进行讨论.

1) 情况1:|i-k|≥2.

首先离散T1, 在区间[xi-1,xi+1]上, 使用插值条件(xi-1,ut(xi-1,tj-1/2)),(xi,ut(xi,tj-1/2)),

(5)

其中ξ=(x-xi)/h. 于是

其中i=1，2,…,k-2,k+2,…,N-1,j=2,3,…,M+1.

(6)

然后在时间方向上用中心差商离散, 得到

其中i=1，2,…,k-2,k+2,…,N-1,j=2,3,…,M+1.

(7)

类似地, 对于T3离散, 得到

其中i=1，2,…,k-2,k+2,…,N-1,j=2,3,…,M+1.

(8)

最后考虑T2的离散,

其中i=1，2,…,k-2,k+2,…,N-1,j=2,3,…,M+1.

(9)

又因为由原方程得:

其中i=1，2,…,k-2,k+2,…,N-1,j=2,3,…,M+1.

代入方程得

(10)

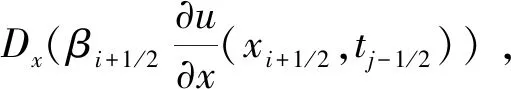
(11)

其中i=1，2，…，k-2,k+2，…，N-1,j=2,3，…，M+1.

(12)

2) 情况2:i=k-1.

由插值多项式

得

(13)

(14)

其中

对于T1的离散:

(15)

T2的离散形式类似于|i-k|≥2的情况, 即把式子(11)、(14)、(15)代入(5), 整理可得

(16)

3) 情况3:i=k.

因为

(17)

利用插值多项式得

(18)

(19)

由(17),(18),(19)整理得

(20)

又因为

(21)

利用方程(4)得

(22)

将(22)代入(21)整理得

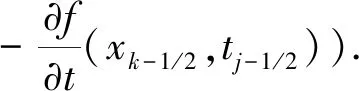
化简得

(23)

又因为

易得

(24)

同理，

(25)

(26)

根据(26), 类似可得T3的离散格式.由(11)得T2的离散格式，将T1、T2、T3的离散代入(5)中得

(27)

4) 情况4：i=k+1. 计算方法同i=k-1时, 利用插值多项式计算系数e,m,n代入(5)得

(28)

其中

由(12)、(16)、(27)、(28)组成了一个线性代数方程组, 该系数矩阵具有很好的三对角性质, 可以用追赶法求解. 具体计算的时候, 右端项中的关于f的积分可以使用两点以上的求积公式: Gauss求积公式或者是Simpson求积公式, 格式形式与紧差分格式近似, 而这种格式是由有限体积方法导出的紧格式, 因而得到高阶紧致有限体积格式.

3 数值算例

取相应的精确解为

则函数f(x,t)和边值条件φ1(x),g1(x),φ2(x)可由u(x,t)相应得到， 应用上述介绍的有限体积格式来计算该定解问题, 其中h=1/M,τ=1/N.取N=M2,下面图1给出了N=M2时差分格式解U的误差和收敛阶的计算结果. 可以看出, 在不同的范数意义下, 空间的误差阶数都达到了四阶或四阶以上. 因此, 时间的误差阶数都达到了二阶或二阶以上, 说明了本文所建立格式的有效性.

图1 N=20, M=400, 间断点为r=3/8时, 数值解与真解的图形

h最大模误差收敛阶L2模误差收敛阶120 3.53e-06— 2.08e-06—1306.68e-07≈4 3.84e-07≈41401.73e-07≈59.81e-08≈51504.62e-08≈62.59e-08≈61601.08e-08≈85.93e-08≈8