新型空间碎片清除平台发射诸元确定及仿真

张治彬，李新洪，安继萍，贺广松，王 谦

（航天工程大学，北京 101416）

0 引言

在科学技术得到了极大的发展之后，人们对这一过程中产生的环境问题的关注度也越来越高。空间碎片分布广泛，数量巨大，对在轨运行航天器造成了致命的威胁。空间碎片危害最大的区域包括由于碎片大量分布的LEO 区域和轨道资源紧缺的GEO 区域［1］。空间碎片主动清除方式主要包括推移离轨、增阻离轨、捕获离轨等。文献［2］对强激光推进空间碎片的烧蚀过程进行了理论推导；文献［3-4］提出了比激光推移更有效的离子束推移离轨；文献［5］验证了膨胀泡沫增阻离轨具有多米诺效应；文献［6］提出了利用静电力降低空间碎片轨道从而实施清除的概念；文献［7］提出一种抛洒人工粉尘使空间碎片轨道降低，加速坠毁的方法；捕获离轨清除是指清除平台与空间碎片物理接触的方式来清除碎片［8］，捕获方式包括机械臂、电动力绳系、容器收集器等。增阻离轨方式适用于LEO 区域小碎片，不适用于摄动力十分微弱的GEO 区域碎片，捕获离轨由于平台机动能力的限制，无法多次进行清除任务，适用于较大碎片，例如失效卫星等。作者在文献［9］中提出一种基于轻气炮载荷的GEO轨道空间碎片清除平台，通过轻气炮载荷定向发射具有额定初速的粘性弹丸与目标碎片发生碰撞，从而将碎片推离原有轨道，达到清除目的。本文利用火控理论对该空间碎片清除平台工作模式进行了建模，利用相对运动方程确定弹丸发射诸元，并通过Matlab 与STK 互联进行了仿真验证。

1 解固定速度增量拦截发射诸元问题

在t0时刻，空间碎片清除平台（简称平台，用P表示）在地球惯性坐标系下位置为RP0，速度为VP0，该平台可发射固定速度大小为dv、方向任意的弹丸（用C 表示），目标航天器（简称目标，用T 表示）位置为RT0，速度为VT0。如图1 所示，在t1时刻，平台调整至期望姿态qd发射出速度为Dv=［Dvx，Dvy，Dvz］T的弹丸，弹丸沿转移轨道运行，在tf（预定拦截时刻）时刻与目标发生碰撞。已知t0时刻平台速度RP0、速度VP0和目标位置RT0、速度VT0以及弹丸速度dv，确定合适的t1以及求解相对应的期望姿态qd和tf，称为解固定速度增量拦截发射诸元问题。把轻气炮载荷通过压缩气体推动弹丸速度增加至dv 称为对弹丸施加单次脉冲，由于对弹丸施加单次脉冲后弹丸可达到的速度大小dv 有限，弹丸可到达范围有限，因此，在施加单次脉冲后弹丸不可到达的区域，需要通过对平台进行合理的机动，使目标进入弹丸的覆盖范围。本文只考虑目标处于弹丸可到达区域内的情况，不需要对平台进行机动，并且在t1=t0=0即发射弹丸。

本文作出以下假设：

1）目标位于弹丸可达范围，平台不需要机动；

2）对弹丸施加单次脉冲，弹丸加速至额定速度的时间可忽略；

3）假设地球为均质球体，不考虑任何摄动；

4）空间碎片清除平台为三轴姿态稳定，且姿态处于理想状态。

2 坐标系统

1）地心惯性坐标系（J2000）：原点位于地心，X轴在赤道平面内指向春分点，Z 轴垂直赤道平面，与地球自转轴重合，指向北极，Y 轴满足右手定则；

图1 碎片清除示意图

2）航天器轨道坐标系（VVLH）：原点位于平台质心，x 轴指向轨道周向，即平台运动方向，z 轴与航天器向径重合，指向地心，y 轴满足右手定则，即轨道面负法线方向。

惯性系到轨道坐标系的转换矩阵为：

式中，Ω 为平台轨道升交点赤经；i 为轨道倾角；u 为纬度幅角。

3）航天器本体坐标系：原点Ob位于平台质心，Xb、Yb、Zb分别于平台的惯量主轴，理想状态下，平台本体坐标系与轨道坐标系重合。

3 相对运动方程

3.1 Hill 微分方程

相对运动方程形式如下：

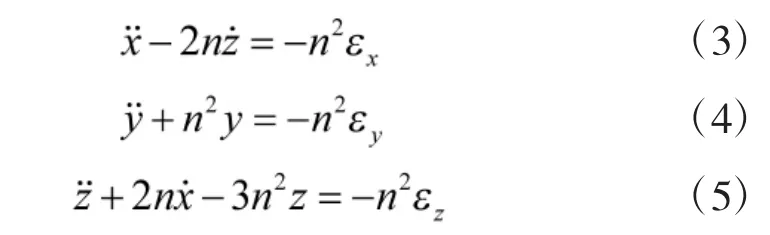
式中

3.2 线性Hill 方程分析解（C-W 方程）

如果平台轨道为圆轨道或者近圆轨道，且目标与平台相对距离远小于轨道高度，则可以忽略非线性项εx，εy，εz，保留线性项得到Hill 方程一阶分析解（C-W 解）。以t1时刻作为初始时刻，t 时刻的状态参数（x y z）可表示为初始状态（x1y1z1）与时间t 的显函数［11］：

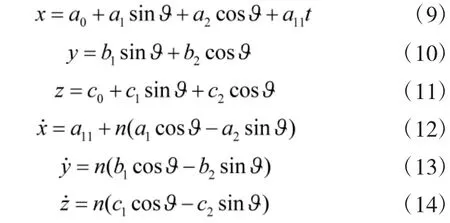
4 发射诸元快速解法

固定速度增量拦截问题中只关心目标相对于平台的位置，以及弹丸相对于平台的位置关系，不考虑相对速度。将式（9）～式（11）改写成函数形式，则在VVLH 坐标系下，tf时刻目标相对于平台位置矢量有：

其中，RT1，VT1分别为惯性系下目标在t1时刻的位置和速度，RP1，VP1分别为惯性系下平台在t1时刻的位置和速度，tf为预定拦截时刻。

t1时刻弹丸的速度Dv=［Dvx，Dvy，Dvz］T，位置为RP1，因此，tf时刻弹丸相对平台的位置矢量表示为：

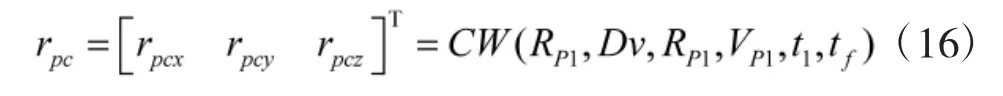
弹丸在tf时刻命中目标，则二者相对于平台的位置矢量相同：

由于弹丸相对平台的速度大小dv 固定，则有：

联立式（17）和式（18）得到四维非线性方程组式（19），4 个自变量分别为Dvx，Dvy，Dvz，tf，因此，方程组存在唯一解或者不存在解（目标位于弹丸单次脉冲可到达区域之外）。

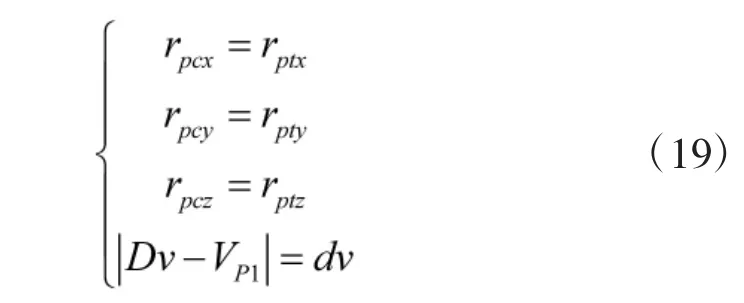
非线性方程组可以使用不动点迭代法、牛顿迭代法等迭代解法，Matlab 中fsolve 函数可以直接对非线性方程组求解，但是fsolve 函数对于初值十分敏感，很容易导致产生局部最优解，并且无法对解的范围进行约束，并且本文需要对预定拦截时刻tf作出限制：tf＞t1＞0。利用最优化解法，将方程组改写为求最小值的目标函数，首先利用粒子群算法得到一个接近于解的搜索初值，然后将目标函数限定为fmincon 的非线性约束，最后利用Matlab 中的GlobaSearch 寻找目标解。

将非线性方程组（19）改写成如下形式，式中第5 项增加了对tf＞0 的约束：

轻气炮安装方向沿空间碎片清除平台本体坐标系Xb轴，平台由本体坐标系绕欧拉轴ObE 转动一次到期望姿态，转动欧拉角φ［12］。欧拉轴ObE 在体坐标系表示为：

其中，xb=［1，0，0］T为ObXb轴的单位矢量在体坐标系下的坐标。则旋转四元数qr为：

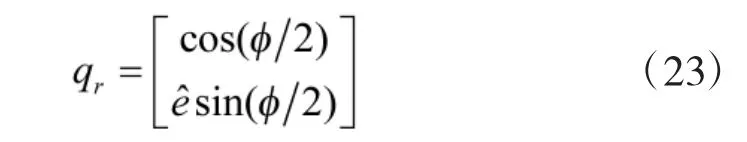
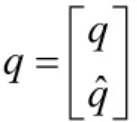
5 算例及仿真

本节利用Matlab 与STK 互联进行仿真验证，给出多组仿真结果并对结果进行分析。本文所用数据均采用国际单位制。惯性系下弹丸轨迹RC（t）到目标轨迹RT（t）间的最短距离矢量作为脱靶量（E）来衡量诸元解算精度［13］，则脱靶量E 的范数为：

在t1=0 时刻，航天器平台位置矢量和速度矢量分别为：

目标位置矢量和速度矢量为：

由式（21）～式（23）确定旋转四元数为：

带入到式（24）可得期望姿态四元数为：

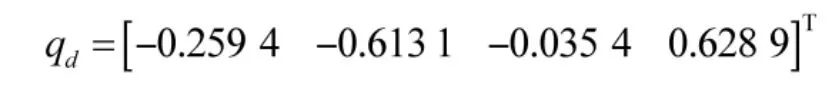
通过STK 仿真得到弹丸和目标的轨迹并带入到式（25）得到脱靶量

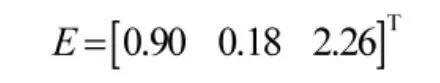
图2 给出惯性系下目标和弹丸相对于平台的位置矢量仿真图，平台、弹丸和目标的轨迹如图3所示。

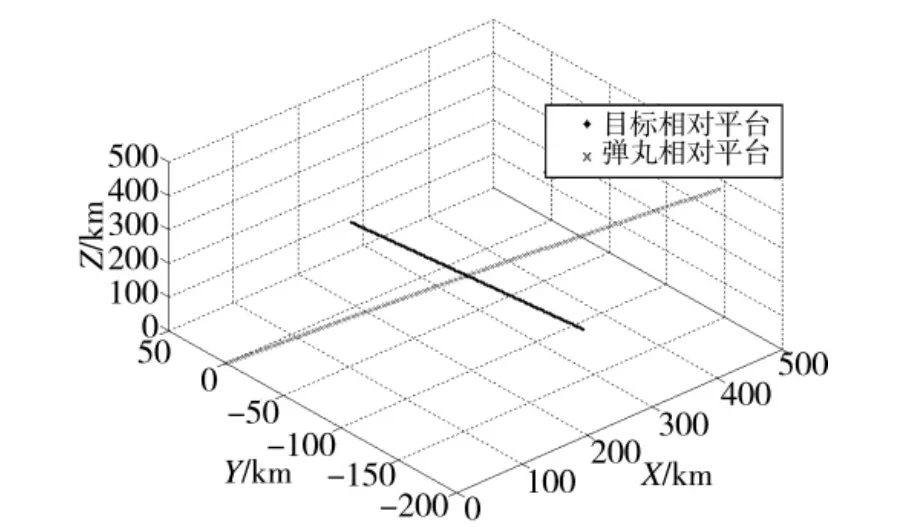
图2 相对运动仿真图

图3 平台、弹丸、目标轨迹仿真图

表1 列出多组仿真结果。可以看出，在平台与目标初始时刻距离|RT1-RP1| 为305 030 m 的情况下，该发射诸元解算算法脱靶量在米的量级，并且随着弹丸发射速度的增加，弹丸飞行时间减小，脱靶量随之减小；脱靶量的产生与C-W 方程线性化条件有关：随着目标与平台距离的增加和平台偏心率的增加，C-W 方程适用于逐渐变差，脱靶量随之增加；除此之外，脱靶量的产生与Matlab 与STK计算精度有关，但是相对于轨道高度而言，软件产生的误差可以忽略不计。

6 结论

本文对基于轻气炮载荷的GEO 轨道空间碎片清除平台发射诸元确定问题进行了研究。在忽略摄动力影响的情况下，利用非线性相对运动方程分析解建立命中方程组，通过最优化方法对方程组求解得到高精度的全局最优数值解。通过STK 进行了仿真验证，仿真结果表明，在初始时刻平台与目标相距300 km 的情况下，脱靶量仅为米的量级，在可接受的范围内，并且弹丸飞行时间为百秒量级，在高轨运行时摄动力可以忽略，因此，新型空间碎片清除平台发射的弹丸可以对目标碎片进行有效的撞击。

由于C-W 解对方程进行了线性化，并且对平台轨道偏心率提出了要求，限制了此解法的使用范围，下一步将利用非线性Hill 方程分析解对问题进行研究。此外，后续将利用仿真实验对弹丸空间散布及命中概率进行分析。

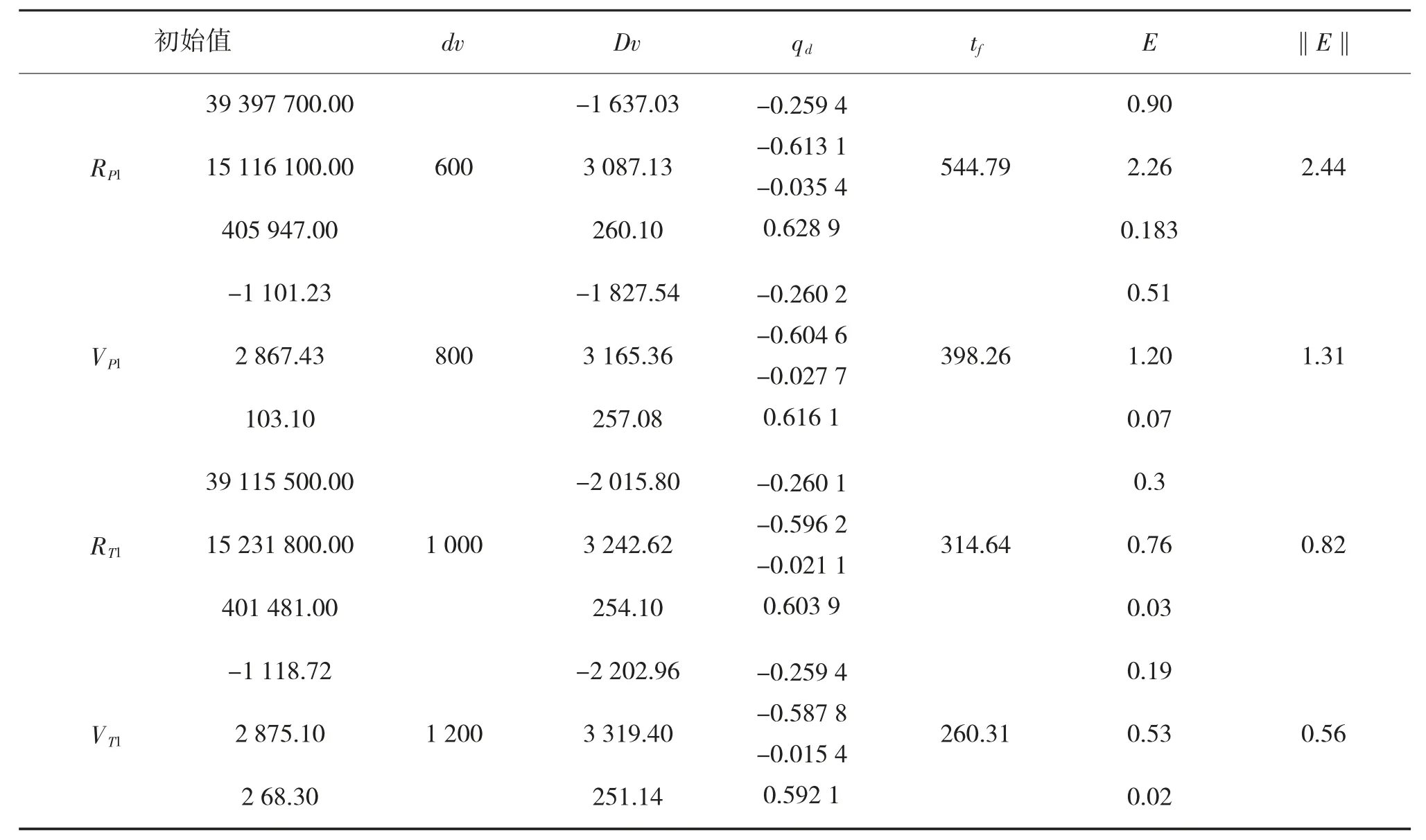
表1 仿真实验结果