卫星单- 混信号识别研究*

彭 闯，杨晓静，蔡晓霞

（国防科技大学电子对抗学院，合肥 230037）

0 引言

成对载波多址（PCMA）复用技术，1998 年由ViaSat 公司的Mark Dankberg 提出［1］，是一种能够有效提高卫星通信容量的新技术。该技术允许通信双方在同一频点发送两路相同调制方式的信号，而后通信双方均接收到相同的混叠后的信号，提高了频带利用率，节省了带宽资源，在卫星通信领域有广阔的应用前景［2］。在协作通信时，由于双方都已知本身的发送序列，并使用自身序列与混合序列相抵消，即可以得到另一方所发送的信息序列。而在非协作通信时，作为第三方接收到混叠后的信号，如何快速对PCMA 信号进行识别、参数估计，以及信号盲分离等成为电子侦察领域研究的关键性问题。而对PCMA 信号调制样式的识别是对其进行后续处理的重要基础［3］。PCMA 信号的出现对原有的卫星信号调制识别算法提出了新的要求，它要能够区分常规信号和PCMA 混叠信号，并对调制类型准确识别。

由于混叠信号的两个子信号分量来自其相应的地面基站，所以两个信号分量的波形、传输时延、载波频率偏移、载波相位偏移都不尽相同，这些原因造成了PCMA 信号在其各种统计量的表现上与单载波信号有本质差距。这也造成了大量的单载波模式识别算法无法运用到PCMA 信号调制样式识别领域。

当前，对PCMA 信号的调制样式识别见诸报道的不多，主要是基于高阶累积量特征、基于谱线特征及基于联合特征参数等来完成调制模式识别。文献［4-7］利用累积量和谱特征等特征参数，完成了对PCMA 混叠信号中相位调制信号的识别，但识别调制样式种类少，限制了其应用范围。文献［8］提出了一种基于累积量和似然特征的卫星单-混信号调制识别算法，但是识别模式太少。文献［9］提出了一种从累积量、谱线、幅度包络平坦度提取特征参数的卫星单混信号识别算法，但算法涉及参数多，复杂度高。

本文针对目前识别存在的不足，利用高级累积量和信号瞬时统计量作为特征参数，提出了一种可行的卫星单-混信号调制样式识别方法，并给出了实现流程。仿真实验表明，在信噪比较低、没有先验信息的情况下，本文算法能够有效地对调制样式为2ASK、BPSK、QPSK、8PSK、16QAM 的单载波信号，及相应的PCMA 混叠信号调制模式进行识别。

1 PCMA 信号模型

PCMA 复用技术在卫星通信链路的示意图如图1 所示［10］。

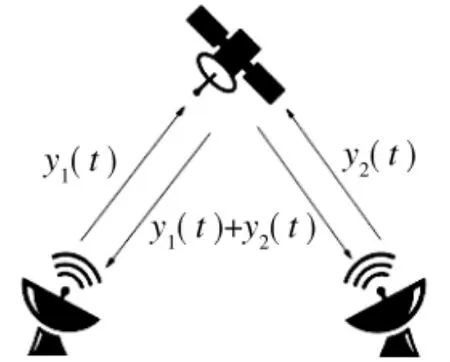
图1 PCMA 信号通信链路示意图

由图1 可以看出，每一个地面基站发送一个上行信号，同时接收到有本地信号和另一地面基站发送的上行信号混叠而成的下行混合信号。两个地面基站发送的上行信号有几近相同的带宽和中心频率，符号的传输速率及基带数字调制方式也相同。PCMA 接收的复基带信号模型可以表示为

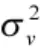
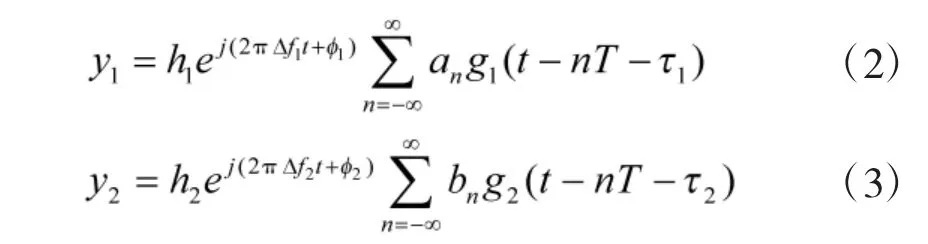
对信号进行过采样处理，采样率为m 倍符号率。由于信号分量是循环周期为T 的循环平稳过程，所以采样后信号成为周期为m 的循环平稳随机序列。

2 调制样式识别原理

2.1 基于高阶累积量的分类特征

高阶累积量可以反映信号的高阶统计特性，虽然计算较为复杂，但有良好的抗衰落特性，因此，常被作为特征量用来完成信号调制识别。对于一个平稳的随机过程xk，其p+q 累积量定义为：

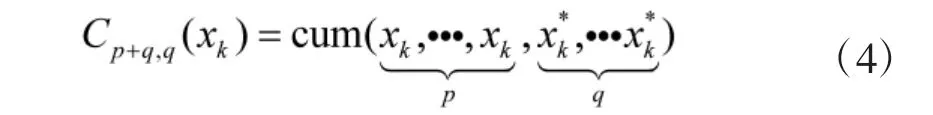
式中，cum（）表示求一个平稳复随机过程的高阶累积量，“*”表示共轭运算。

假设单载波信号的每个符号间隔的平均能量为E，四阶累积量的值与E2成正比。数字调制信号累积量的理论值如下页表1 所示［11］，其中混叠信号混合幅度比值取1∶1。

其中C21表示信号的平均能量，故使用其对信号进行能量归一化［12］。

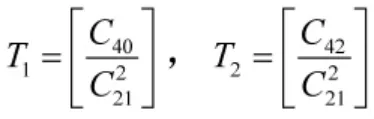
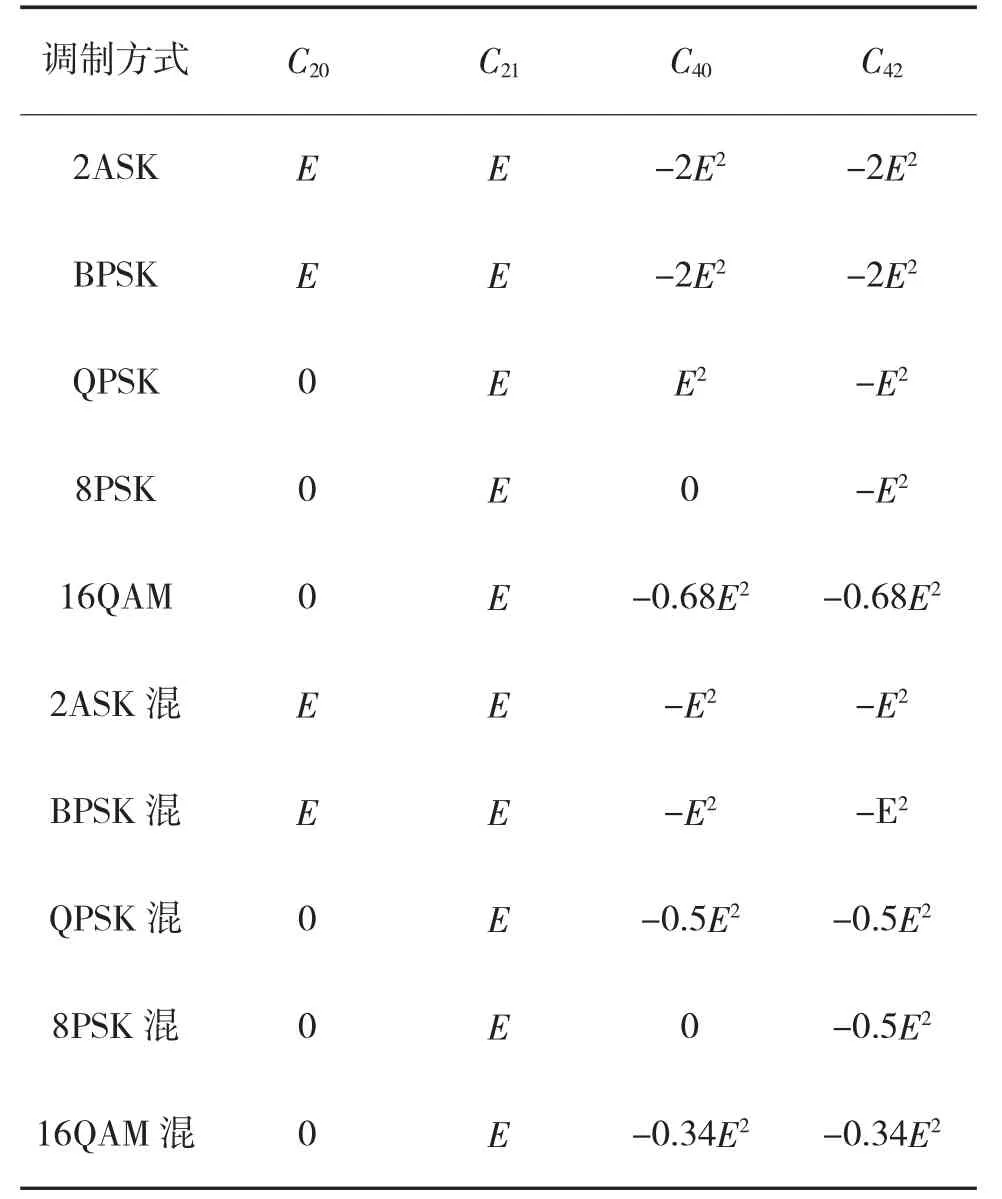
表1 数字调制信号累积量的理论值

对于特征参数T1、T2，选择信噪比范围为0 dB～20 dB，对每个信噪比处取100 次实验，每次实验取样本L=5 000 个符号。特征参数T1、T2随信噪比变化曲线如图2 所示。

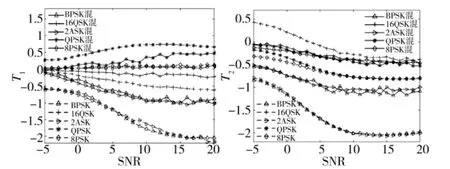
图2 T1、T2 随信噪比变化曲线（幅度比1∶1）

2.2 基于信号瞬时特征统计量的分类特征

高阶累积量构造的特征参数无法将各调制样式分离，引入有瞬时特征统计量构造的特征参数T3=σdp，T4=σap。T3=σdp为零中心瞬时相位非线性分量的标准偏差，σdp表征信号瞬时相位的变化情况。T4=σap为零中心瞬时相位的非线性分量的绝对值的标准偏差，σap表征信号的绝对相位变化信息。使用σdp来完成{BPSK、2ASK}及{BPSK 混、2ASK 混}信号的模式识别。使用σap来完成{QPSK 混、8PSK 混}信号的模式识别。

2.2.1 瞬时信息

为了方便调制信号的瞬时幅度、瞬时相位、瞬时频率特征值的提取操作，首先给出实信号的解析表示：

其中，y（t）为实信号x（t）的希尔伯特（Hilbert）变换：

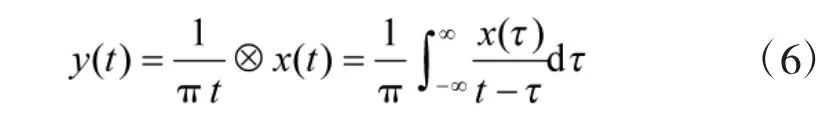
其中，“⊗”表示卷积操作。以抽样频率fs对实信号x（t）进行抽样，得到序列x（i），得其复解析式为：

其中：

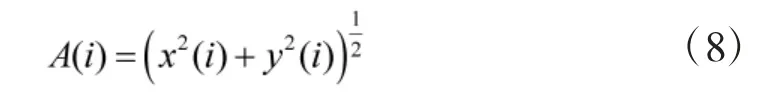
即信号的瞬时幅度序列。

反正切函数的取值范围为（-π/2，π/2），所以瞬时相位序列θ（i）的计算表达式为：

又由于θ（i）具有折叠相位，取值范围仅在（-π，π），因为是模2π 计算的，想恢复出无折叠相位，需要引入相位序列修正量，现定义相位序列修正量C（i），其计算方法如下：

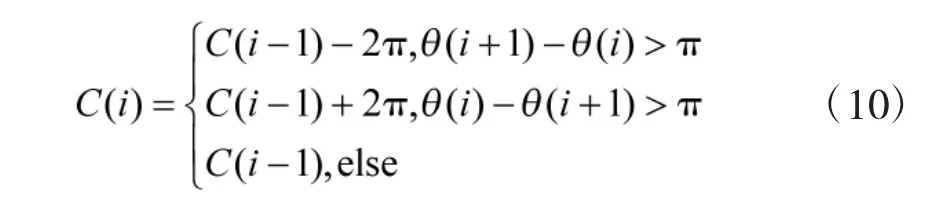
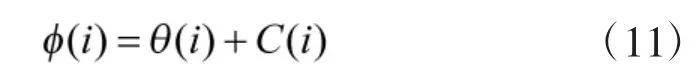
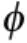
2.2.2 零中心瞬时相位非线性分量的标准偏差

选择使用零中心瞬时相位非线性分量的标准偏差σdp分离{BPSK、2ASK}、{BPSK 混、2ASK 混}两个集合中的信号，因为在BPSK 中含有直接相位信息，而2ASK 中不含直接相位信息，用该统计量完成这两种调制样式的识别。下面给出具体的计算公式：

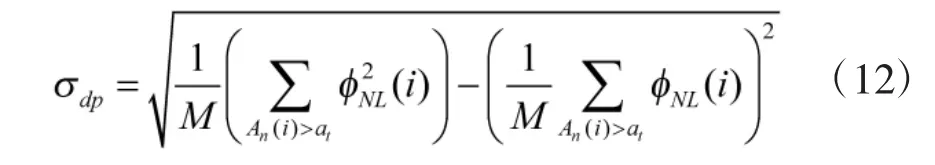
选择信噪比范围为0 dB～20 dB，对每个信噪比处取100 次实验，每次实验取样本L=5 000 个符号，特征参数T3=σdp随信噪比变化如图3 所示。

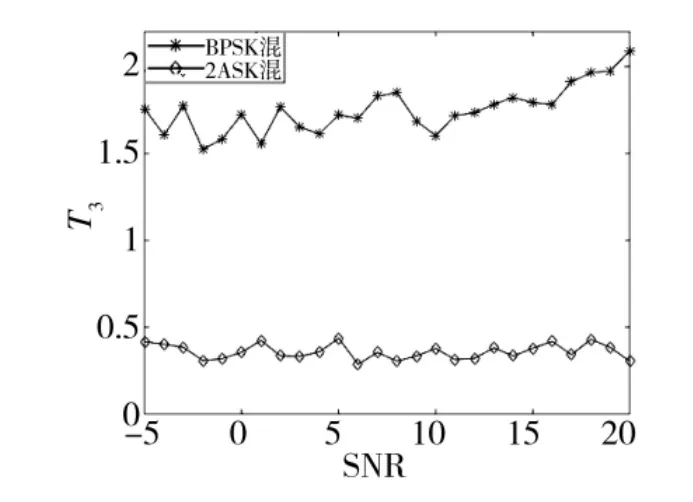
图3 T3 仿真曲线（幅度比1∶1）

对混叠信号将非弱信号瞬时幅度门限设为1.2，降低了信号波形间的相位积累及失真对特征参数的影响。由图3 可以看出随信噪比增加，两条曲线变化趋向平缓，易于区分，当t（σdp）＞1，信号调制样式BPSK 混叠信号，当t（σdp）＜1，调制样式为2ASK混叠信号，验证了特征参数T3的适用性。文献［16］完成了对单载波调制样式为2ASK、BPSK 的T3的仿真实验，可以完成对调制样式的识别。

2.2.3 零中心瞬时相位的非线性分量绝对值的标准偏差

选择零中心瞬时相位的非线性分量的绝对值的标准偏差σap，作为第4 个特征参数实现{QPSK混、8PSK 混{信号的模式识别。σap为瞬时相位的非线性分量的绝对值的标准偏差，表征信号瞬时绝对相位的变化情况。其具体计算公式如下：

PCMA 混叠信号的8PSK 混、QPSK 混调制样式在该特征参数上有明显差异，8PSK 混应明显大于QPSK 混。特征参数T4=σap随信噪比变化如图4所示。

图4 T4 仿真曲线（幅度比1∶1）

由图4 可知，在QPSK、8PSK 调制下PCMA 混叠信号有不同的值，可以完成得QPSK 混、8PSK 混信号的识别。随信噪比增加两信号的值区别增大。当t（σap）＞0.3 时，信号调制样式为8PSK 混，当t（σap）＜0.3 时，信号调制样式为QPSK 混。

本文在计算特征参数T3、T4的值时，为减少计算数据长度，提高计算速度，对信号进行分段求值，再求平均的做法，提高运算速度，同时也降低了特征参数T3、T4值的随机性误差。

3 识别方案

3.1 决策树分类器设计

数字调制信号使用二进制随机序列作为信号源，模拟信号使用正选模型，干扰为AWGN 噪声，根据所设计的特征参数对信号进行识别，决策数分类器如图5 所示。

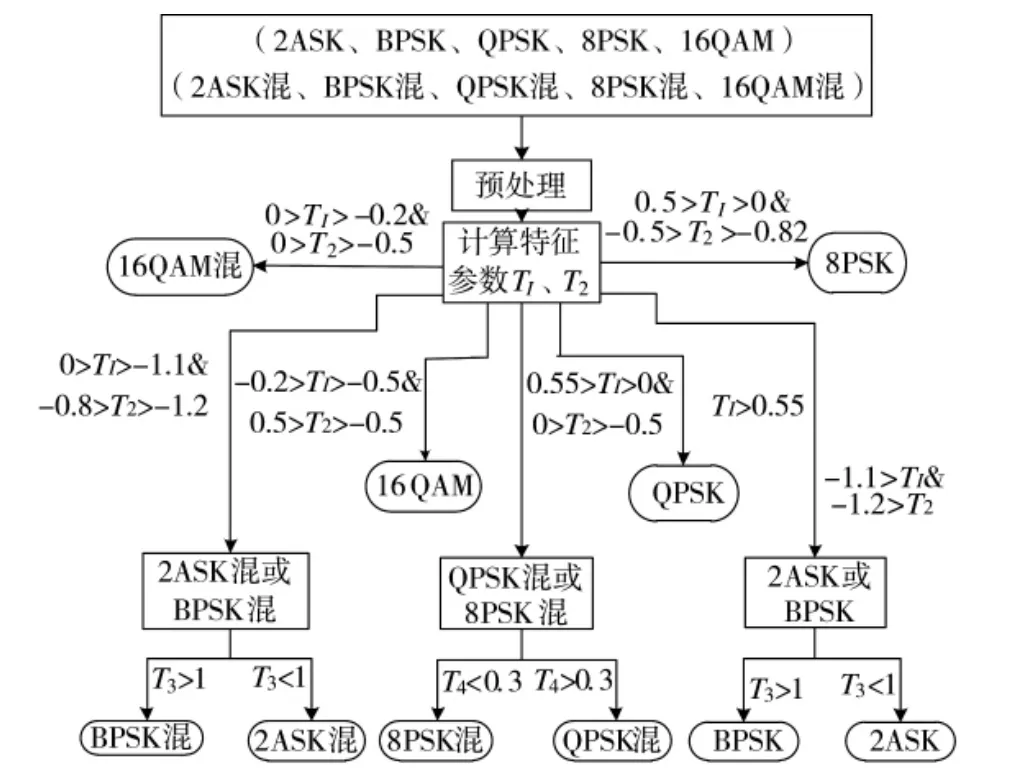
图5 调制模式识别流程图

3.2 识别流程

通过上述提出的4 个特征参数，完成对备选的调制样式为{2ASK、BPSK、QPSK、8PSK、16QAM}的单载波信号与PCMA 混叠信号的特征识别，具体流程如下：

1）对接收到的信号进行下变频及过采样处理，得到预处理后序列y（k）。

2）对y（k）求取特征参数T1、T2，设置门限值如图5 所示，完成对信号调制模式的第1 次识别，识别出信号调制样式为QPSK，或者是16QAM，或者是8PSK，或者是16QAM 混，或是属于子集S1={2ASK、BPSK}，或是属于S2={2ASK 混、BPSK 混}，或是属于S3={8PSK 混、QPSK 混}。若属于子集S1、S2跳转至步骤3），若属于子集S3则跳转至4）。若识别结果是QPSK、16QAM、8PSK 或16QAM 混，则跳转至步骤5）。

3）计算信号序列的瞬时信息，完成特征参数T3=σdp的计算，t（σdp）＞1 为BPSK 或BPSK 混信号，t（σdp）＜1 为2ASK 或2ASK 混信号。跳转至步骤5）。

4）计算信号序列的瞬时信息，完成特征参数T4=σap的计算，t（σap）＞0.3 调制样式为8PSK 混信号，t（σap）＜0.3 调制样式为QPSK 混信号。

5）识别完毕。

4 仿真实验

对预处理得到的差分序列y（k），根据识别方案进行实验。改变信噪比，每信噪比进行1 000 次蒙特卡洛实验，对结果取平均值，得到的识别率如表2所示。

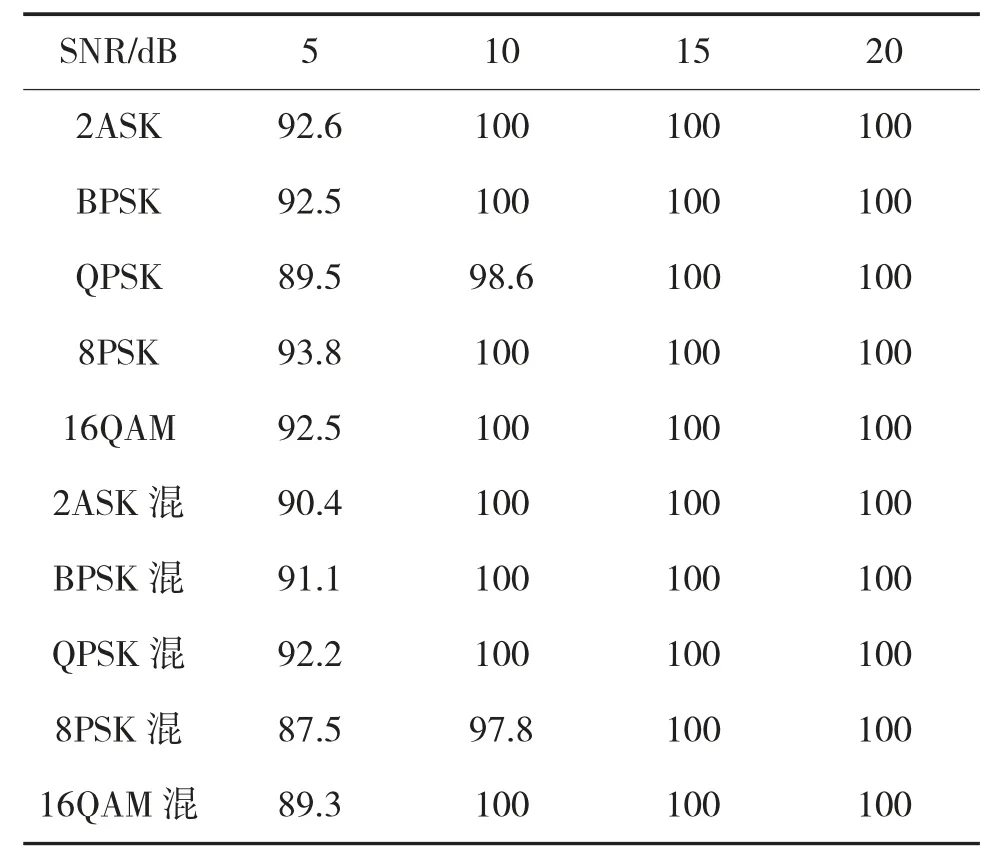
表2 调制识别算法识别率（%）

由表2 可以看出，考虑存在信号的频率偏移、相位偏移等参数的影响下，在信噪比5 dB 时正确率识别都超过了85%，具有较高的识别率。

对于PCMA 混叠信号系统，子信号的混合幅度比对信号调制样式识别的成功识别有重要影响。为验证算法在混合幅度比变化的情况下的识别性能，将预设门限值带入算法，在信噪比为10 dB 情况下，混合幅度比取0.6～1，在每一处幅度比进行1 000 次蒙特卡洛实验，对实验结果取平均值，结果如表3 所示。

表3 调制识别算法识别率（%）

由表3 可以看出，该算法在信噪比为10 dB，幅度混合比0.8 时，正确识别率大于95%。

实验验证了本文算法的适用性和稳定性。与文献［7］相比，识别调制样式种类明显增加，扩宽了算法的应用范围。与文献［8］相比，本文算法有更高的识别率，正确识别所需的信噪比有所降低。与文献［9］相比，虽识别率大致相同，但本算法识别信号调制样式种类更多，且只使用了高阶累积量和瞬时特征统计量两类信号特征，证明了本文算法的优越性。

5 结论

本文针对卫星通信中常用的单- 混信号的调制模式识别问题进行了研究，提出了一种基于高阶累积量和信号瞬时特征统计量的识别算法。该算法运算速度快，在不需知道信号的大量先验信息的条件下，为完成对卫星常用调制信号和PCMA类混叠信号的调制模式识别提供了一种解决途径。但是在本文中，只考虑了在高斯信道中的性能，对复杂噪声及衰落信道情况下的算法实现还有待继续研究。