基于EML 模型的备件库存优化方法*

王 莹

（湖北第二师范学院数学与经济学院，武汉 430205）

0 引言

随着国际局势日益复杂多变，国际问题日渐矛盾化、复杂化和尖锐化，国防建设迫在眉睫，装备保障能力是军队战斗力的重要分量，而备件则是装备保障能力的一个关键要素。如何保持和快速恢复作战装备执行使命任务的作战能力离不开维修保障，而备件保障又是维修保障工作中的重中之重，其已经成为装备作战性能生成的核心组成部分，与作战性能居于同等重要的地位。备件保障领域被很多学者广泛使用的METRIC模型［1］，假设前提之一是所有备件重要性相同，后续很多学者进行了跟进研究，见文献［2-19］。

上述文献都在某方面取得了一定成果，但在具体工程应用中存在如下问题：1）若考虑备件重要性之后，这些问题METRIC 模型将无法解决，但这些问题在实际的工程实践中比较常见，值得进行深入研究；2）边际效应法是备件领域被很多学者常常使用的方法，但当备件重要性不同时，该方法将无法再使用，需要对其进行改进和提高；3）将备件重要性和备件配置优化中的约束条件两者联合起来进行相关研究的文献比较少，很多文献只是侧重约束条件或备件重要性两者中的一个方面；4）由于保障经费有限，装备仓库不能无限制地配置所有需要的备件，这就需要将有限的经费在保障那些重要性备件的同时兼顾重要性一般的备件。

本文建立了备件重要度的评价指标和求解过程，给出了装备可用度增量和边际效应模型，改进了边际效应法，并给出了解决该类问题的流程图，构建了EML 模型（Experts Grading Method、Marginal Effect Method、Lagrange Multiplier）并用案例进行了验证和说明。

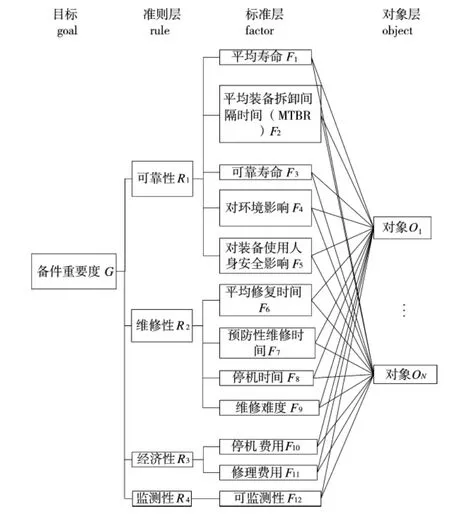
图1 备件重要度的层次分解

1 备件重要度的评价指标和求解过程

1.1 备件重要度的评价指标

备件重要度的评价指标共有4 个准则层，分别为：可靠性（R1）、维修性（R2）、经济性（R3）和监测性（R4），4 个准则层又可以按如下分为12 个重要度指标：

1）平局寿命（F1）。装备在实际工作中寿命分布为一个随机变量，其数学期望就是装备的平均寿命，对于可修复装备平均寿命称为平均故障间隔时间，对于不可修复装备而言称为平均无故障工作时间。不同装备平均寿命单位不同，例如车辆和坦克为里程、飞机等航空航天装备为小时（h）、舰艇用的舰炮为发数等等。本文根据选择装备的具体情况分为6个等级，以小时（h）为单位，等级1 为大于10 000 h，分值为1；等级2 为（6 000，10 000］，分值为2；等级3 为（2 000，6 000］，分值为4；等级4 为（500，2 000］，分值为6；等级5 为（100，500］，分值为8；等级6 为小于100，分值为10。

2）装备拆卸平均间隔时间（F2）。该时间主要是指除了装备升级改造及为了别的修理活动开展的需要，在装备全寿命时间内除以装备的拆卸次数。本文将其分为6 个等级，以h 为单位，等级1 为小于0.5 h，分值为1；等级2 为（0.5，1］，分值为2；等级3 为（1，1.5］，分值为4；等级4 为（1.5，2］，分值为6；等级5 为（2，3］，分值为8；等级6 为大于3 h，分值为10。

3）可靠寿命（F3）。装备按上级要求在规定的时间和强度下完成使命任务的能力，其主要通过可靠度来衡量，对可靠度有一定要求的装备，到了规定的工作时间就要进行更换，否则便会影响任务成功性。本文依据可靠度要求的大小将其分为5 个等级，等级1 为大于0.95，分值为1；等级2 为（0.85，0.95］，分值为4；等级3 为（0.75，0.85］，分值为7；等级4 为（0.6，0.75］，分值为9；等级5 为小于0.6，分值为10。

4）装备故障对环境产生的影响（F4）。装备故障对周围环境的影响主要是由其特殊的物理或化学特性引起的，包括毒性和腐蚀性等。本文依据装备故障对环境的影响分为4 个等级，等级1 为没有影响，分值为1；等级2 为对环境影响较小，分值为4；等级3 为对环境影响较大，分值为7；等级4 为造成严重环境污染，分值为10。

5）对装备使用人员人身安全的影响（F5）。当某装备故障后是否会间接造成爆炸及有毒物质泄漏等，以及装备故障的影响范围及对装备使用人员的影响，如日本核电站的核泄漏情况。按对装备使用人员的影响分为4 个等级，等级1 为没有影响，分值为1；等级2 为对装备使用人员和设备安全影响轻微，分值为4；等级3 为使用人员和设备安全影响中等，分值为7；等级4 为使用人员和设备安全影响严重，分值为10。

6）故障平均修复时间（F6）。装备从故障状态到修复完好时间的期望，在装备整个寿命周期费用内是所有修复时间之和除以修复次数，影响因素主要包括装备故障诊断确定时间、故障排除时间、修理准备时间、装备拆解及重新安装时间、安装调试时间等，但不包括备件管理和供应延误时间，相同装备故障不同的修理级别修复或不同的修理条件也可能会导致修复时间有很大差别。依据故障修复时间分为6 类，单位为h，等级1 为小于0.5 h，分值为1；等级2 为（0.5，1］，分值为2；等级3 为（1，3］，分值为4；等级4 为（3，6］，分值为6；等级5 为（6，12］，分值为8；等级6 为大于24 h，分值为10。

7）预防性修理时间（F7）。装备平均预防修复时间是每次修复时间的期望，不包括装备边工作边修理的时间和上级仓库备件供应延误的时间。依据预防性维修时间分为6 类，单位为h，等级1 为小于0.5 h，分值为1；等级2 为（0.5，2］，分值为2；等级3 为（2，4］，分值为4；等级4 为（4，8］，分值为6；等级5 为（8，12］，分值为8；等级6 为大于12 h，分值为10。

8）停机时间（F8）。装备停机时间主要指从装备发生故障到修理工作开始启动的时间，体现了对人力资源和保障经费的需要程度，不仅和维修性有关，同时也和可靠性有关。依据停机时间分为6 类，单位为h，等级1 为小于0.5 h，分值为1；等级2 为（0.5，1］，分值为2；等级3 为（1，12］，分值为4；等级4 为（12，24］，分值为6；等级5 为（24，148］，分值为8；等级6 为大于148 h，分值为10；

9）修理难度（F9）。故障修理部分维修装备的位置不同，其修理难度可能会存在很大差异，如舰艇上的装备故障后，因受仓库空间的限制会比陆地上的装备维修起来难度比较大一些。依据故障修理的难易程度不同分为4 类，等级1 为容易，分值为1；等级2 为一般困难，分值为4；等级3 为比较困难，分值为7；等级4 为非常困难，分值为10。

10）停机费用（F10）。主要指装备故障后续无法继续完成上级赋予的使命任务带来的损失，如战争时期因为某项备件缺失，导致作战舰艇无法使用，那么带来的损失是用钱无法来估量的。依据停机费用的不同划分为4 个等级，单位为万元，等级1 为小于1 万元，分值为1；等级2 为（1，10］，分值为4；等级3 为（10，50］，分值为7；等级4 为大于50，分值为10。

11）维修费用（F11）。主要包括人力资源费用、备件购置费用及材料费用。依据修理费用的不同分为6 个等级，单位为万元，等级1 为小于500，分值为1；等级2 为（500，1 000］，分值为2；等级3 为（1 000，5 000］，分值为4；等级4 为（5 000，10 000］，分值为6；等级5 为（10 000，50 000］，分值为8；等级6 为大于50 000，分值为10。

12）可监测性（F12）。对于航空航天类装备其对可靠性要求非常之高，要求可以实时监测到装备技术状态，主要通过安装压力传感器、温度传感器等各种监视传感器实现。依据监测要求的不同，分为4个等级，等级1 为低，分值为1；等级2 为一般，分值为4；等级3 为高，分值为7；等级4 为非常高，分值为10。

1.2 备件重要度的求解过程

备件的重要度仅仅依靠说明书提供的数据是有所欠缺的，必须在静态数据的基础之上依据一些装备实际工程实践中的动态数据进行综合确定，同时采用主客观相结合的方法，即一方面依据装备工程实践中的指标，另一方面聘请相关领域的专家和装备实际使用人员对装备重要度进行打分，同时根据专业水平和装备使用经验赋予不同打分人员不同的权重，最后综合所有可能的情况得到备件重要度。

一般来说备件重要度应由相关领域的专家、相应装备的使用人员及专业维修人员根据备件的12个指标确定，为了克服专家打分法的缺点，依据不同类型人员赋予不同的权重，最后将所有备件重要度进行归一化处理，构成列和为1 的向量，处理之后的数据能够相对比较准确体现12 个指标之间的差异性，具体计算流程如下所示。

Step1：构建m 个备件和n 个指标之间的（xij）m×n矩阵。

式中，m 为设备数量；n 为指标数量。

Step2：在矩阵（xij）m×n的基础之上，l 个不同领域的专家和专业人员依据n 个指标给备件的k 个重要度进行打分，构成（yij）l×k矩阵。

式中，l 为专家和专业人员的数量；k 为备件的重要度数量。

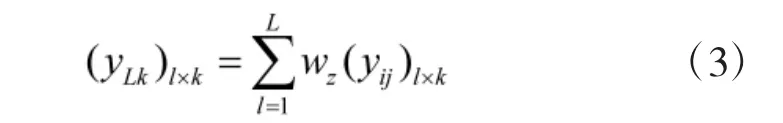
式中，Yk为L 个专家针对某备件重要度的打分分值之和。

Step5：依据式（3）的结果，构建备件重要度的标准化向量，并进行归一化处理。

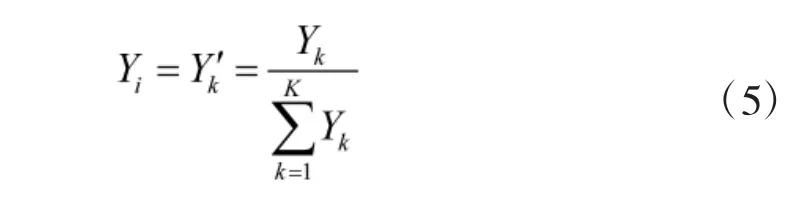
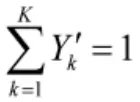
2 装备可用度建模

2.1 装备可用度模型

1）期望短缺数EBO

当装备因为故障出现故障需要时，但仓库却没有备件，此时便记为1 次备件短缺，即：

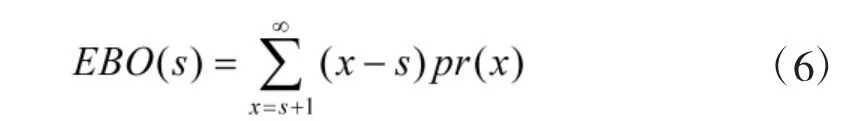
式中，s 为需要的备件在仓库中存储的数量；pr（x）为上级仓库即将补充备件的稳态概率分布；从Plam 定理的数学角度可知，pr（x）服从泊松函数分布，即

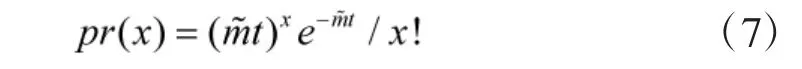
其中：

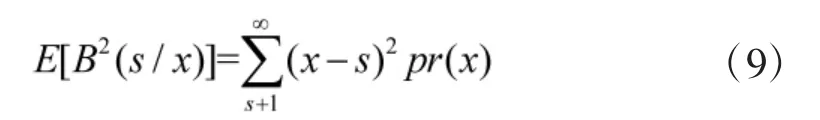
2）装备可用度

依据METRIC 模型和装备的修理参数，可以求出装备的可用度，即

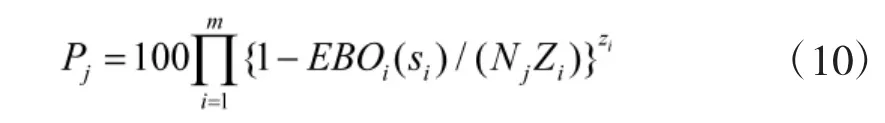
式中，Nj为设备j 在装备上的安装个数；Zi为备件i在单个装备上的安装个数；Pj为装备可用度；式（9）成立的前提条件必须满足备件重要度相同，且不进行备件的横向供应或故障件的串件拼修。

对式（15）两边取以e 为底对数，即

对式（10）取以e 为底的指数，适当变形可得到：

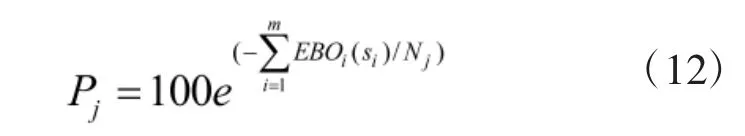
2.2 装备可用度的增量模型

假设为保障上级赋予使命任务的完成，在有限的保障经费控制范围内，在原有备件的基础之上，每增加一个备件携带，此时用该备件产生的备件短缺数的降低量或者可用度的增加量除以“边际成本”即可得到“边际效益”值，可用ΔEBO 或ΔP 表示，即

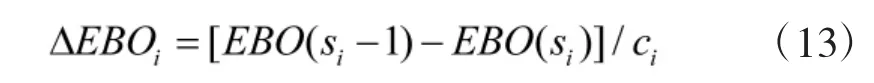
式中，ci为边际成本。

装备可用度按式（12）进行适当调整即可得到，即

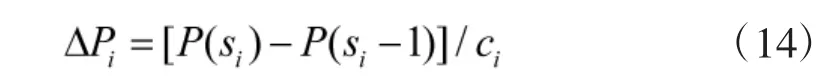
2.3 基于备件重要度的边际效益模型

在不考虑备件重要度的情况下，按2.1～2.2 节的模型和方法，可以求出备件携带方案，但在实际工程实践中，备件的重要性显然是存在差异的，必须要对2.1～2.2 节模型和方法进行适当调整，使其更加符合工程实践需要。

在1.1～1.2 节基础之上，将得到的备件重要度和2.1～2.2 节模型进行结合即可得到新的边际效益值，即

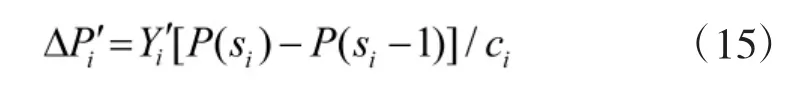
式中，ΔA'为考虑备件重要度后新的边际效益值。

除去误报警、零位漂移等因素的影响，依据给定的修理参数，可以求出设备的需求率mi，即

式中，MTBFi为故障间隔时间、Zi为设备单机安装个数；Ti为装备执行任务周期中实际使用时间。

3 模型建立

模型的建立主要分为3 个方面：约束条件和目标函数、模型求解和模型建立。

3.1 约束条件、目标函数和模型建立

1）约束条件和目标函数

约束条件和目标函数，依据决策的侧重点不同，可以在一定条件下相互转化，依据不同的工程实践情况可以有不同的组合，但本文提供的方法和模型依然适用，求解步骤的本质是相同的，只要适当变换即可。

因仓库空间有限，不能无限制地存储所有需要的备件，如舰船上的仓库空间，故在制定库存方案时，需要考虑仓库空间的最大值，即

式中，vi为需要的备件占用空间的大小；Vt为仓库空间能容纳备件体积的极限值。

决策者在制定备件库存方案时比较关心在满足可用度最低要求时，此时装备的备件库存方案和保障经费。

式中，Ps为库存系统方案下的装备可用度；P0为决策者对装备可用度的最低要求。

因保障经费有限，导致无法购买所有需要的备品备件，需要进行优化，使保障效益最大化，重点照顾重要性高的备件的同时兼顾重要性一般的备件，即

式中，ci为备件i 的购买单价；Ct为上级给定保障经费额度。

2）模型建立

决策者一般比较关心在满足装备可用度最低要求的情况下，最优保障经费或者在给定的保障经费条件下装备能够达到的最优可用度，这两个问题的本质是一样的，因篇幅有限，本文只选择一个问题进行研究，即

3.2 模型求解

模型求解主要包括8 步，具体如下：

Step1 从1.1 节可知，此时输入变量不止一个，需要引入拉格朗日乘子法，将其变成一个综合约束因子，即

Step2 将备品备件的体积因子和费用因子转化成综合约束因子后，此时装备可用度可以依据综合约束因子表示为：

对式（22）两边同时取以e 为底的对数，即

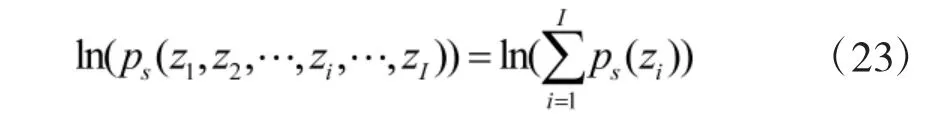
Step3 计算在某约束条件下的备件携带方案，计算此时可约束指标为满足要求时的实际值大小，引入拉格朗日乘子法，求出约束条件因子，以保障费用为例进行说明，即

Step4 此时，依据式（21）计算得到综合约束因子的矩阵为：

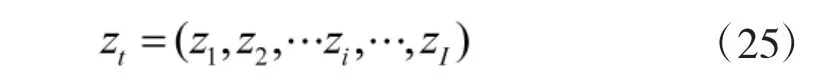
Step5 对式（23）进行适当数学变换可得边际增量为：

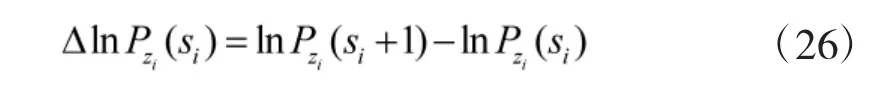
Step6 依据式（24）～式（25），进行适当数学变换可以得到边际效益值，本文用Δ 表示，即

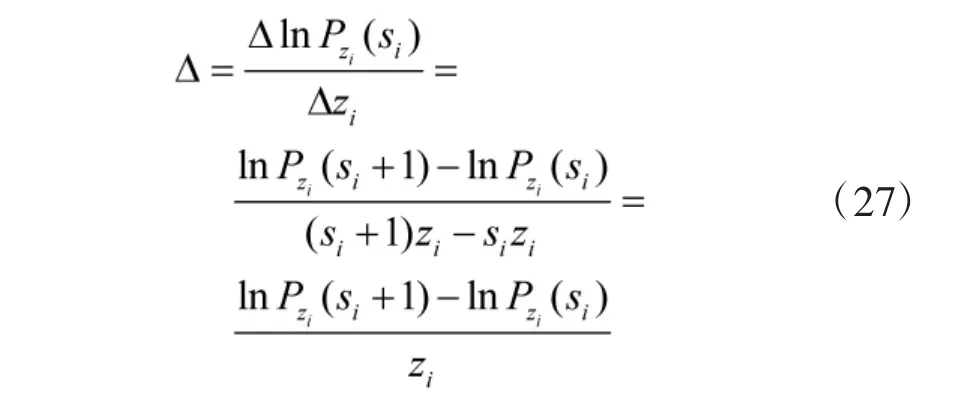
Step7 计算在给定目标函数下约束指标需要的最优值，和给定的指标上限进行对比，判断其是否超过，若未超过，则运算结果为最优方案；若超过，则需要更新综合约束因子或者增加指标值大小，即

Step8 依据式（24）～式（25）重新计算边际效益值，即

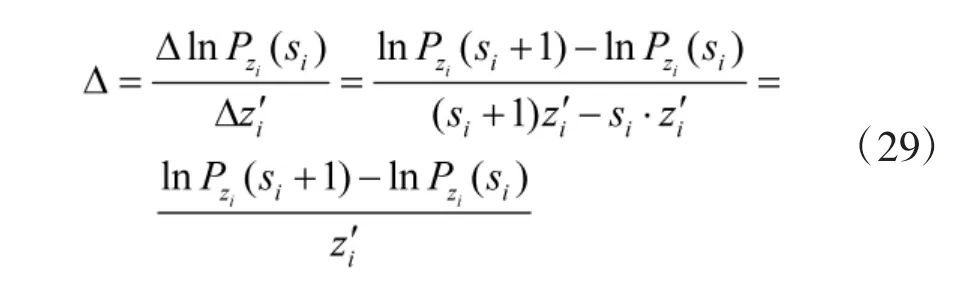
Step9 重复Step6～Step8，直到得到满足全部指标要求的方案为止。

4 实例分析

本文以某新型装备备件清单为研究对象，因其备件数以万计，且本文的主要目的在于介绍方法和求解思路，故本文选取其中比较有代表性的10 个电 子 类 备 件（LRU1、LRU2、LRU3、LRU4、LRU5、LRU6、LRU7、LRU8、LRU9、LRU10）作为研究目标。

假设装备要执行为期3 个月使命任务，装备每天平均要工作20 h，则3 个月共工作1 800 h；10 个装备在某新型装备上的安装数量都为1 个，10 个装备的平均故障间隔时间为（1 984、1 755、572、753、1 005、1 930、2 300、1 355、2 032、2 968）备件的购置费用分别为（0.91、0.15、0.38、0.65、0.31、0.45、0.28、0.76、0.55、1.12），单位为万元；10 个备件的体积大小 为（0.83、1.23、0.88、0.11、0.15、0.33、0.72、0.29、0.27、0.31），单位为m3；以任务周期记，10 个备件供应 周 期 分 别 为（0.08、0.09、0.09、0.08、0.67、0.09、0.09、0.12、0.14、0.09），单位为h。

聘请1 名教授、2 名副教授和2 名装备使用人员，赋予权重为（0.3、0.2、0.2、0.15、0.15），按上述给定的修理数据，结合1.1～1.2 节内容，计算得到10个备件重要度分别为（4.21、5.1、4.43、4.51、5、4.51、5.24、4.95、4.93、5.12），进行归一化处理，得到（0.087 8、0.106 3、0.092 2、0.093 9、0.104 2、0.094 1、0.109 2、0.103 1、0.102 6、0.106 6）。

假设上级对装备可用度最低要求为95%，仓库空间为20 m3，计算此时最优保障费用，采用MATLAB 程序进行计算，当循环36 次时，装备可用度为94.33%，不满足要求，当循环37 次时，装备可用度为95.06%，满足要求，此时备件方案为（4、2、2、2、5、4、5、4、4、5），需要的仓库空间为19.22 m3，此时最优保证经费为16.59 万元，具体情况如图2 所示。

以上述方案为基础，依据2.1～2.3 节模型和求解步骤，求出10 个备件的综合约束因子为（1.682 2、1.294 5、1.198 8、1.682 8、0.449 6、0.757、0.949 9、1.03、0.801 2、0.408 4），引入求出的10 个备件重要度，当循环24 次时，此时装备可用度为94.98%不满足要求，循环到25 次时，此时装备可用度为95.32%，满足要求，可求出此时备件配置方案为（2、1、1、1、3、3、3、3、3、4），需要的仓库空间为11.4 m3，此时最优保证经费为10.53 万元，具体情况如图3 所示。

将图2 和图3 进行对比分析可知：图3 的方案比图2 的方案更加优化。图2 的方案是在考虑装备可用度和仓库空间大小的情况下得到，满足决策者要求，但却没有考虑备件重要性；图3 是在图2 计算的基础之上，考虑了备件的重要性，将图2 中的备件储存方案进行了进一步的优化，从计算结果已经证明了图3 思路是更优化的方案。

图2 10 个备件的费效曲线

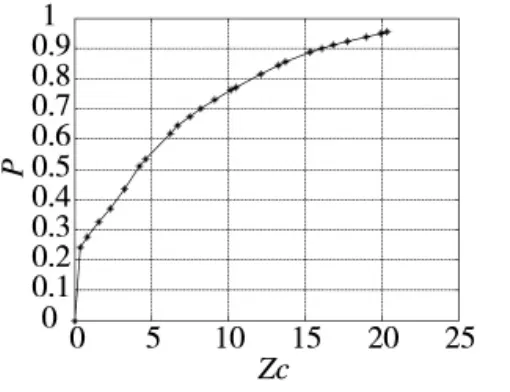
图3 基于备件重要度的10 个备件携带方案

5 结论

1）给出了备件重要度的12 个评价指标，并给出了备件保障领域专家依据其求出备件重要度的方法和模型；

2）将边际效应法进行了改进，对其适用范围进行了拓宽，使其在重点兼顾重要度比较高的备件的同时，兼顾重要度一般的备件，在保障经费比较紧张的条件下，具有非常大的经济效益；

3）本文重点给出了当备件重要度不一致时的边际效应法改进办法，并给出了解决问题的办法和求解步骤。在具体的工程实践中重要度指标可以适当调整，可以增加或删减一些指标，但具体求解问题的方法和模型步骤依然适用；

4）当问题有单层级变化成多层多级时，模型和方法将变得更加复杂，同时求解难度将继续增大，这类问题将是后续研究的重点关注领域，