基于活动环路的作战网络节点重要度评估方法*

2019-09-17李清韦刘俊先

火力与指挥控制 2019年8期

李清韦，刘俊先，陈涛

（国防科技大学系统工程重点实验室，长沙 410073）

0 引言

随着复杂网络理论的广泛应用，在作战体系结构领域常用网络测量方法对作战体系节点进行评价，利用度指标、介数指标、紧密度指标和特征向量指标对作战节点的重要性进行定量分析，判定体系对抗中的关键点［1-2］。在作战网络中找出这些关键点是至关重要的，一方面可以重点保护这些关键点提高整个作战网络的可靠性，另一方面也可以攻击这些关键环节达到摧毁整个网络的目的。

根据OODA 环理论，指挥控制作战的特点就是按照观察-判断-决策-行动（OODA）环路进行的战斗［3-4］，作战网络中必然存在很多环。而现有的网络测量方法，如节点收缩法［5］、节点删除法［6］、效率矩阵法［7］等，在对作战节点评估时重点考量环路的情况较少，不太符合指挥控制作战的特点。文献［8］提出一种基于闭路径检测的环排名度量，但评估结果不够精细，不易判断相似节点的重要程度。本文针对这一情况，提出了一种基于作战活动环路的作战网络节点重要度评估方法。通过对作战活动及作战活动间的关联关系构建作战网络模型，根据作战网络中作战活动构成的环路改进了介数方法，定义环介数、依赖关系和影响因子3 个指标对作战网络节点的重要度进行定量分析，通过算例分析验证了该方法的有效性，为作战网络提供了一种合理实用的作战节点重要度评估方法。

1 理论基础

本文研究的是作战网络节点的重要度。为了评估节点重要度，建立作战网络模型是基础。而网络是由节点和边构成的，对作战网络的建模离不开抽象节点与边。因此，主要工作一是要根据体系任务分解得到作战活动，分析作战活动之间的关联关系，构建作战网络模型；另一个是要根据作战特点及节点关系定义评估指标，评价作战网络，对作战网络节点的重要度定量分析，用具体的数值来表示作战网络节点的重要度。

1.1 作战网络建模

本文研究的作战网络是基于作战活动和作战活动之间的关联关系所抽象出来的网络，因此，只有对作战过程中的各要素进行抽象的描述和定义，才能确定构建作战网络的节点和边。任务和功能分解的最终结果就是具体的作战活动［9］，将作战活动和作战活动之间的联系抽象成作战网络模型，区别于传统的利用IDEF0 方法对作战活动进行建模。

作战网络的节点：在作战过程中，完成作战使命或任务要进行一系列的作战活动。根据任务和功能对作战活动进行分解，可得到最底层的活动。将作战过程中一系列的最底层作战活动抽象为作战网络的节点。

作战网络的边：一个作战活动向另一个作战活动传递的命令、信息或者数据等可以抽象成为一条单向边，边的箭头则代表信息交互的方向为从箭头的起点到箭头的终点。所有作战活动之间的关联关系就构成了作战网络的边。

作战网络模型：一个具有n 个作战节点的作战活动网络可用G=（V，E）表示，其中V=（v1，v2，…，vi，…，vn）是作战网络的节点集，E=（e1，e2，…，ei，…，em）是作战网络的边集。活动网络G 是一个把活动作为节点、把活动关联关系作为边的有向图。图中的节点代表活动，边代表所连接的两个活动间存在的关联关系。图G 相对应的邻接矩阵用01 矩阵A表示，A=［eij］n×n，其中

1.2 评估指标定义

定义1 环介数（Loop Betweenness）：作战网络中节点vi的环介数就是作战网络中所有环路与通过该节点vi环路数量的比例，节点vi的环介数lbi形式化表示如下：

其中，numi表示经过节点vi的环路数目，m 表示作战活动网络的环路总数。

定义2 依赖矩阵（Dependency Matrix）D：作战活动环网络中节点之间有直接依赖关系或间接依赖关系，用D=［actij］n×n表示作战活动的依赖矩阵，其中的actij表示作战活动actj对acti的依赖程度。用dij表示同时经过节点vi和节点vj的作战活动环路中，节点vi到节点vj的最短距离，则节点vj对节点vi的依赖程度可用1/dij表示。节点对自身的依赖程度为1，即1/dij=1。若节点vi和节点vj之间无环路，则两点之间的距离无穷大。作战网络节点依赖矩阵形式化表示如下：

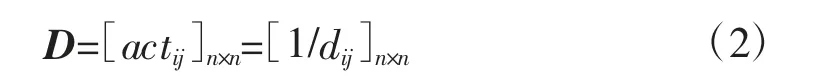
定义3 影响因子（Impact Factor）K：根据网络科学对距离的考虑，两点之间的边数越多，说明两点越难以到达［10-12］。在作战网络中，完成作战任务的环路边数多，说明环路经过的作战活动多，代表这条环路作战效能低。也就是说，环路的边数越多，这条环路所代表的作战活动中受到破坏或阻碍的可能性越大，影响环路上活动顺利完成的因子也越高。因此，可以用影响因子k 来描述影响环路中作战活动顺利完成的各种不确定性。节点vi的影响因子ki形式化表示如下：

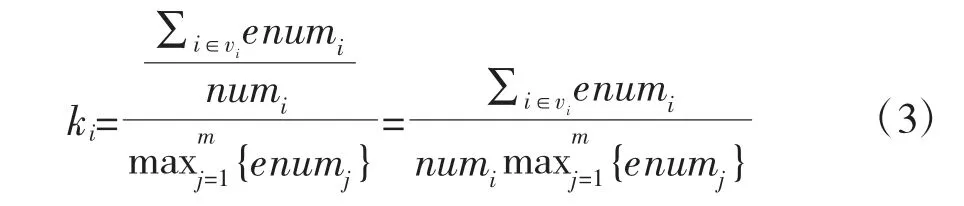
1.3 指标合理性分析

在对节点进行评估时，本文主要考虑了环介数、依赖程度和影响因子3 个因素。不同的节点其环介数也不一样，对其他节点的影响程度也不尽相同。节点环介数越大，对作战环路资源的控制能力越强，对其他节点的影响也越大。因此，将环介数作为重要度的基础指标是合理的。

节点的入度被定义为节点依赖的节点的数量，而出度被定义为依赖于节点的数量。入度的高值表明该节点高度依赖于其他节点。元素的出度是衡量节点的关键度。节点的依赖矩阵即表示了节点对其他节点的依赖度，也可以表示节点的关键度。作战活动之间存在多种关系，活动之间的依赖关系可以判断作战活动的关键度。故将依赖矩阵作为评估节点重要度的一项指标是有效的。

作战网络中的作战活动间关系构成环路简化了路径选择的控制，但作战网络中某条环路上各作战节点间是直接串联的，这样任何一个节点出了故障都有可能造成整条环路的中断。如果作战环路的边数较多，作战环所面临的风险和不确定性也随之增加，在作战时被破坏或阻碍的概率也会较大。环路越长越容易遇到随机性、模糊性、粗糙性和不精确性等影响，此时将影响因子作为评估节点重要度的指标也是恰当的。

2 节点重要度评估算法

2.1 评估算法

针对作战网络具有OODA 环的特点，本文提出基于作战活动环的作战网络节点重要度评估方法，弥补了文献［8］中只考虑环路边数而造成评价结果不准确的不足。文中选取节点间形成的环路由作为节点间相互作用最主要的作用路径，环介数表示节点对作战资源的控制，依赖矩阵表示节点间的依赖关系。因此，网络中节点相对于其他节点的重要度可以用矩阵H 表示，即

本文在考虑节点相对重要度的基础上，结合环路边数大小带来的影响，在作战时环路易受到破坏的风险程度和不确定性，可以定义节点的重要度集合IMC 为

节点重要度与环介数值是成正比的，环介数越大节点越重要；与节点的被依赖程度成正比，节点被其他节点依赖的程度越高越关键；与节点的影响因子是成反比的，影响因素越多节点效能越低。节点vi的重要度imci为

用maximc表示节点重要集合中最大的值，用minimc表示最小的值，则归一化后的节点vi的重要度为

2.2 评估流程

基于上述对节点重要度的评估思想，建立本文面向作战活动的作战网络节点评估机制，其主要过程如下：

1）根据作战使命任务和作战过程，确定并分解至最底层的作战活动；

2）根据作战活动之间的关联关系，建立作战网络模型，将作战网络模型转换为邻接矩阵；

3）找出网络中所有环路，统计经过各个节点的环路，计算各节点的环介数；

4）统计节点间在环路上的距离，计算节点间的依赖程度；

5）根据节点的环介数和依赖矩阵，计算节点的相对重要度；

6）统计环路的边数，找出最大环路，计算节点影响因子；

7）计算节点的重要度，归一化后对节点进行排序。

2.3 算法复杂度分析

基于作战活动环评估作战网络节点的重要度是全局性的，查找网络中的环路时要对所有的作战节点进行遍历。本文采用深度优先遍历算法，对某一节点进行深度优先遍历时，要依次搜索该节点的每个邻接点，直到所有和该节点有边相连的节点都被访问过。某一节点完成深度优先遍历要将网络中所有的相连节点遍历一次，而文中构建的网络最多有n2条边，故每个作战节点的计算复杂度为O（n2）。当依次遍历完n 个作战节点时，总的计算复杂度为O（n3）。

3 实验分析

3.1 OODA 环分析

依据OODA 环，对敌作战活动主要可分为观察、判断、决策和行动。OODA 环模型如图1 所示，首先探测系统将观察和探测的目标信息传递给情报中心进行判断和处理；其次情报中心形成态势信息上报指控中心进行决策，并将目标信息发送到火力打击平台；接着，指控中心根据态势作出决策，将打击命令发送到打击平台，并将指控信息发送到探测系统和情报中心；最后，火力打击平台按照指控中心命令，根据探测系统的导航信息，对目标实施火力打击，并将打击效果反馈给探测系统和指控中心。观察、判断、决策和行动每个活动之间都存在着关联关系，这4 个活动极具重要性，传统方法难以分辨它们的重要程度，本文提出的方法很好地解决了这个问题。利用本文提供的方法计算这4 个活动的重要度，结果如图2 所示，4 个活动的重要度值较为接近，但略有差异，行动的重要度最高为3.88，其次是决策活动，重要度值最小的是判断活动，仅为3.17。通过分析，验证了本文提出方法的可行性，并且具有较高的精确性。

3.2 实例分析

本文以防空作战为例，对本文提出的算法进行了验证。根据防空作战指挥流程，防空作战包括目标探测、信息处理、威胁评估、计划决策和火力打击等作战活动［13］，将它们分解至最底层的作战活动得到目标搜索v1、原始数据处理v2、探测控制处理v3、接收目标数据v4、目标信息处理v5、目标类型识别v6、计算威胁等级v7、作战态势估计v8、火力分配v9、火力打击v10等活动。将上述10 个活动从1～10 分别编号，构建的作战活动网络模型如图3 所示。

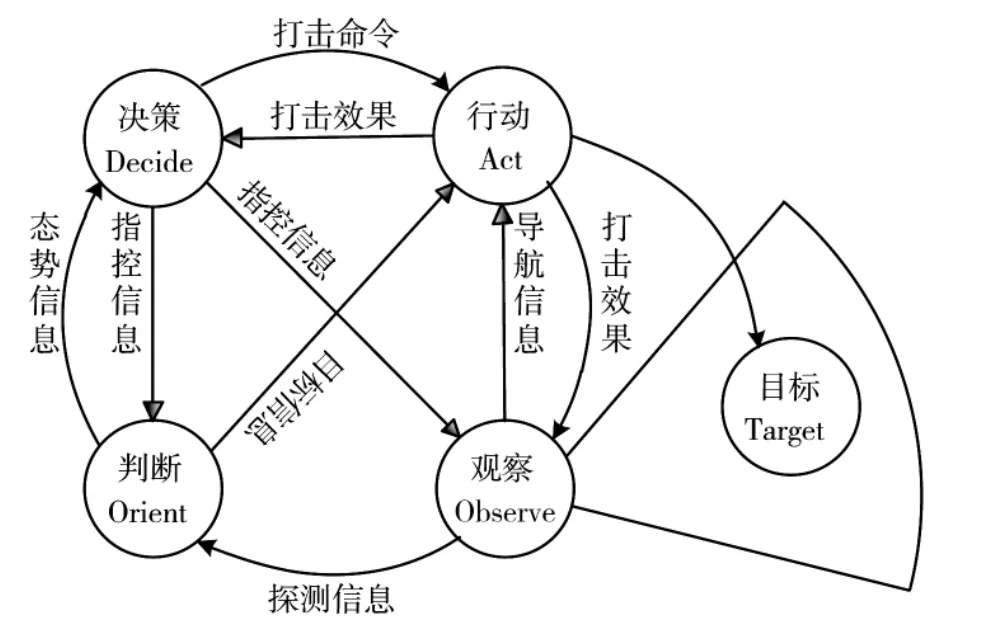
图1 OODA 环示意图

图2 OODA 环节点重要度

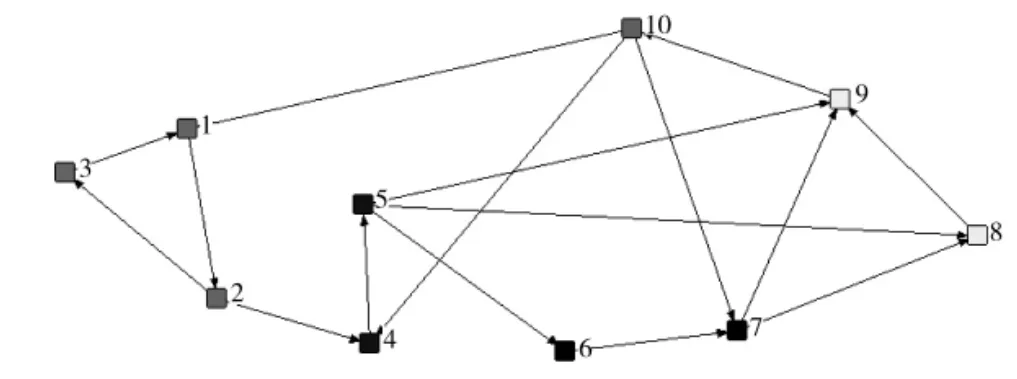
图3 作战网络模型

图中共有10 个节点，16 条边，构成了11 条作战环路。经过节点v9和v10的环路最多为10 条，经过节点v3环路最少只有1 条。最长的环路为v1→v2→v4→v5→v6→v7→v8→v9→v10→v1，其边数为9；最短的环路为v1→v2→v3→v1，其边数为3。根据本文提供的算法，具体的计算结果如表1 所示。

表1 节点重要度计算结果

由表1 可知，节点v10的重要度值最高，即火力打击活动是最为重要的。防空作战的最终任务是拦截敌来袭火力，也就是实施火力打击，故关键活动是火力打击。其次是节点v9，目标信息处理活动。重要度最低的是节点v3，探测控制处理活动，因为这是一种辅助活动，只是为了更好地实施目标探测活动。由此可知，本文提出的方法计算所得的结果符合实际情况。

若只考虑环介数这一因素，节点v1、v2和v3，节点v4和v5，节点v9和v10的环介数值是相等的，无法比较它们的重要性。若只考虑影响因子，无法比较节点v1和v2，节点v4和v5，节点v9和v10受影响的程度。故将多个指标综合考虑以确定节点重要度的方法更为合理有效。

3.3 算法准确性分析

表2 节点重要度评估结果

为充分说明本方法的有效性和准确性，对上述作战网络采用3 种方法进行重要度测定，其结果见表2。从表2 中可见，各方法对节点重要度的评价存在些许差异，排序也稍有不同，评估指标选取的不同造成了这种差异，但采用本文方法能更精确反映节点的属性特征。介数法和文献［7］方法认为节点v1和v2，节点v4和v5，节点v9和v10的重要度是相同的，而根据本文提供的算法，这几个节点的重要程度是有区别的。说明本文设计的方法对节点的区分度更高，对作战节点重要度的评估具有良好的精度，能显著地区分作战网络节点间的重要度差异。但该方法存在一个限制是它只是基于环，若是无环网络则无法进行判断。