基于VMD 与数学形态学分形维数的战场声目标识别*

张 坤，顾晓辉，邸 忆

（南京理工大学，南京 210094）

0 引言

现代陆地战场中，坦克与直升机成了主要武装力量，它们火力猛、机动性强并具有很好的装甲防护能力。这两者的声信号具有短时、强噪声、非线性、非平稳且无先验信息的特点［1］。小波与经验模态分解（EMD）是处理非平稳信号的常用方法，主要思想是将信号分解为各个频率分量再进行处理。但小波需确定基函数，故适应性较差；EMD 存在模态混叠现象［2］，分解的精度会受影响。2014 年由Dragomiretskiy［3］等人提出的变分模态分解（VMD），将信号通过自适应维纳滤波组，分解可得到调频-调幅性质的模态分量［4］。其方法具有良好的理论依据，能成功地将两个频率相近的谐波信号分离，在自适应与分解精度上要优于前两种方法。

为了提高快速性，可利用分形维数特征来描述一维信号［5-9］。分形维数有容量维数与信息维数，通常用盒计数法计算。盒计数法采用了规则划分网格的方式，导致分形维数估计不够准确且计算量大。

针对不同战场声学目标的识别问题，以分形维数为特征向量利用BP 神经网络对声目标进行识别，达到对声目标快速识别的目的。由于文献［8］提出的EMD 与盒计数法融合的方法是目前运用分形与信号分解工具处理非平稳、非线性信号的常用方法，将该方法与本文提出的方法在信号分解质量、特征提取的可分性以及声识别效果上进行对比，说明了文献［8］方法在处理声信号方面的不足，而本文方法更具有优势。

1 变分模态分解方法

VMD 方法是将原信号f（t）在变分框架下，分解为k 个估计带宽和最小的模态分量。类似于EMD称为本征模态分量函数（IMF）。

模态分量的表达形式如下：

对每个IMF 进行单边希尔伯特变换，得到信号单边频谱，然后调制到估计的中心频率上，通过解调获得各个模态的带宽，最后通过调节信号的高斯平滑来估计信号的带宽和，即为梯度的二范数的平方，构造出如下变分模型：

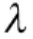
将式（3）变换到频域，求极值得到IMF 的uk（t）与ωk（t）的表达式：

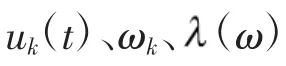
2 数学形态学分形维数计算方法

数学形态学的基本运算包括腐蚀与膨胀［10］。设f（n）和g（m）分别定义在F={0，1，2，…，N-1}和G{0，1，2，…，M-1}的离散函数，且N＞＞M，f（n）为输入信号，g（m）为结构元素。

则f（n）关于g（m）的腐蚀定义为：

则f（n）关于g（m）的膨胀定义为：

采用这两种运算可构筑信号的轮廓线，从而完整覆盖信号，为分形维数的计算提供基础。

假设离散时间信号f（n），n=0，1，2，…，N，单位结构元素定义为g，在尺度ε 下所用结构元素定义为：

则信号在尺度ε 下的形态覆盖面积Ag（ε）为：

根据容量维数定义可知：当ε→0 时，有如下满足关系：

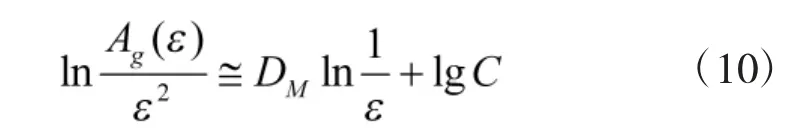
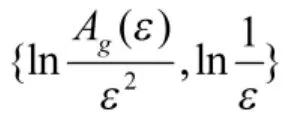
单一容量维数仅考虑了覆盖的个数，而未考虑每个覆盖中包含结构元素的个数分布。根据在不同尺度ε 下对信号f 的膨胀与腐蚀定义，可定义一个反映结构元素分布函数Pi（ε）：

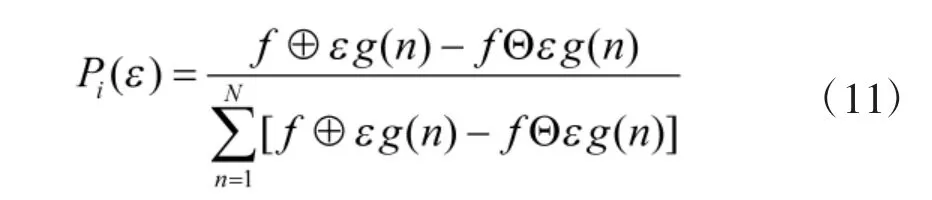
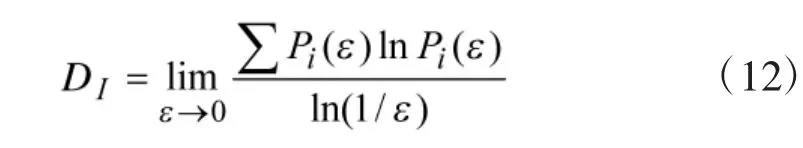
和计算容量维数一样，采用最小二乘法拟合数据点，即可得信息维数DI。

3 基于VMD 与数学形态学分形维数的战场声目标识别方法

结合VMD 与数学形态学分形维数，提出的声目标特征提取方法的步骤如图1 所示：

步骤1：获取声信号，对信号进行频谱分析，确定能量的主要集中频段0～fmaxHz。

步骤2：对信号进行VMD 分解，初始化分解的IMF 个数k=2，惩罚因子α 与带宽使用默认值α=2 000=0。

步骤3：以步骤2 中的参数进行分解，观察各IMF 分量中心频率最大值ωk与主要能量集中频段的关系，若在频段区间内即ωk＜fmax，则可继续分解；若ωk＞fmax，则IMF 个数为k。

步骤4：确定结构元素g 与尺度ε，对分解出的IMF 分量进行膨胀与腐蚀运算，根据式（9）得到各IMF 分量的形态学覆盖情况。

步骤5：改变分解的尺度ε，根据式（10）～式（12）计算各IMF 分量容量维数与信息维数。

步骤6：分别对多段坦克与直升机声样本重复上述步骤，将该段声信号的各个IMF 的容量维数与信息维数作为特征向量。

步骤7：将提取出的特征放入BP 神经网络分类器中进行训练、测试，检验识别效果。

4 实例分析

4.1 目标声信号的VMD 分解

采用声传感器对这两类声音进行采集，采样频率为20 kHz。对这两类声信号进行频谱分析，测量信号长度为1 024 个采样点。原始目标信号与相应频谱如图2 所示。

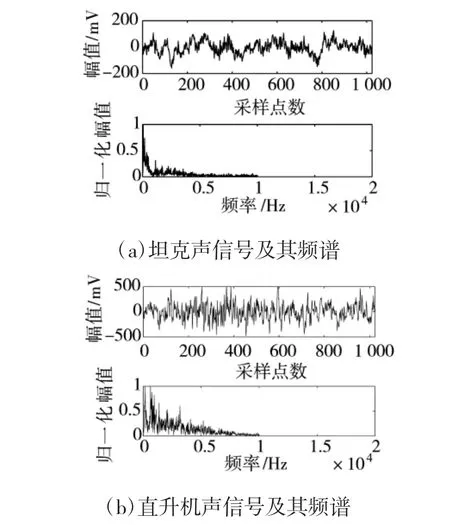
图2 战场声信号与相应频谱

通过两者频谱图可知，坦克与直升机声的主要能量集中在0～3 000 Hz 左右，故由VMD 分解产生的IMF 分量的频率范围应在0～3 000 Hz。VMD 分解需要确定分解的IMF 数量k，数量太少，会导致分量混叠，数据会失真；分解IMF 数量过多，又会造成运算量增大，不利于快速识别。通过中心频率来估计IMF 的分解数量。当IMF 的中心频率超过3 000 Hz时即停止分解。对直升机与坦克声信号进行VMD分解，得到各模态中心频率如表1 所示。

表1 坦克与直升机声不同k 值对应的中心频率

由表1 可知，当坦克声IMF 个数为4 时，最高中心频率达到7 500 Hz，超过3 000 Hz，而当IMF 个数为3 时，最高中心频率为2 988 Hz，接近3 000 Hz，故IMF 分量数为3 是最合适的。表1 中直升机声信号VMD 分解的IMF 个数为3 与4 时，最大中心频率接近3 000 Hz，且两者差距不大，故可认为已经过分解［10］，则IMF 个数确定为3。

对一组典型的坦克声作VMD 分解得到各模态信号，并与EMD 分解方法进行对比图3 与图4 为VMD 分解和EMD 分解后的信号与频谱图。

图3 坦克声VMD 分解后信号及相应频谱

图4 坦克声EMD 分解后信号及相应频谱

将图3（b）与图4（b）对比，EMD 各模态存在明显的频谱混叠现象。分量C1与C2在1 000 Hz～3 000 Hz 存在混叠，而C2与C3在0～2 000 Hz 存在混叠。而VMD 各分量几乎不存在混叠现象，各IMF分量分别代表0～1 000 Hz、1 000 Hz～2 500 Hz 与2 500 Hz～4 000 Hz不同频段的信号分布。同时EMD会分解出较多的IMF 分量，而VMD 的分解数目可根据需要设定，相对EMD 计算量更小。

4.2 分形维数的形态学计算

通过VMD 分解后，坦克与直升机声信号均被分成3 个代表不同频段的IMF 分量，为获取信号分形维数特征，利用数学形态学方法计算各IMF 分量的容量维数与信息维数。运用数学形态学方法估计分形维数时，关键是单位结构元素的选取与尺度的选择。为减小运算量且提高覆盖信号的质量，结构元素选择矩形结构g={1，1，1，1，1，1}。在尺度选择上，因为是线性拟合，采用连续取值会造成计算量较大，故尺度采用离散化取值，最大尺度要求不超过信号长度的一半［11］。本文设置的尺度为［2，4，8，16，32，64，128，256］。

图5 坦克声IMF1 信号形态学覆盖

对信号进行形态学覆盖，图5 为选取尺度8 与32 的结构元素对坦克声分量IMF1 的形态学覆盖结果。图5 中下方黑线为信号腐蚀的结果，上方黑线为信号膨胀的结果，这上下两组信号即对信号形成形态学覆盖。再由式（10）与式（12）的线性关系进行最小二乘拟合，得到基于数学形态学的容量维数与信息维数。选择10 个典型坦克声样本与10 个直升机声样本计算各自模态的两种维数，并用文献［8］的方法与本文结果进行比较得到如图6 与图7所示的数据分布。

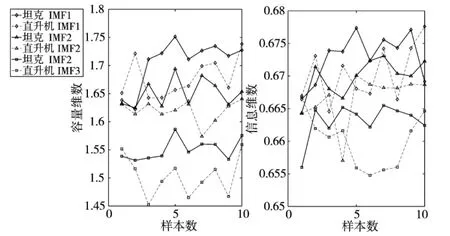
图6 文献［8］方法计算所得不同目标形态学分形维数分布

图7 本文方法计算所得不同目标形态学分形维数分布

将图6 与图7 对比，本文方法提取的特征向量具有更好的区分性，采用文献［8］提取的两类声信号特征则容易形成维数混叠。由图7 得到直升机声各IMF 的容量维数与信息维数均大于坦克声相应IMF的维数，具有较好的区分性，故以VMD 分解出的各IMF 分量的两种维数构建的声特征向量，能够较好地区分不同类型的声学目标。此外，形态学方法仅需要进行加减运算，比盒计数法具有更快的运算速度。

4.3 目标识别精度分析

表2 采用本文方法提取的特征向量

从这140 组声音中随机抽取70 组作为训练集，剩下70 组作为测试集，识别结果如表3 所示。由表3 识别结果，运用本文方法提取的特征对两种声信号进行识别取得了较高识别率，分别达到了97.2%与91.2%。而采用文献［8］的方法在同等条件下，识别率为67.2%与78.3%，本文方法的识别率要高很多。同时由于VMD 与数学形态学方法结合相对于EMD 与盒计数法的优越性，计算的效率与准确度也更高。因此，本文提出的识别方法是一种较好的选择。

5 结论

表3 两种方法的坦克声与直升机声识别结果

根据战场声信号能量主要集中频段，本文运用变分模态分解将信号分解为3 个IMF 分量；相比EMD 分解方法，VMD 分解出的各IMF 分量不存在频谱混叠且分解的IMF 数能够调整，节省计算量的同时得到更精确的分解结果。运用数学形态学方法计算了两类声信号各个IMF 的容量维数与信息维数，相比盒计数法计算的维数，具有更好的区分性和更快的速度。利用BP 神经网络分类器进行比较，得出了更高的识别率且运算速度更快，体现了基于VMD 融合数学形态学的声目标识别方法的优越性。