计算碳原子半径的一种新方法

何 帅,李 斌,田凤阳,王文山,石小利

(1.宝鸡雍城中学,陕西 宝鸡 721400;2.陕西省化学反应工程重点实验室(延安大学)陕西 延安 716000;3.延安职业技术学院,陕西 延安 716000)

原子半径是描述原子结构的基本参数,影响和决定了体系的很多性质 ,在物理和化学领域中有广泛的应用 .通常用共价半径,离子半径和范德华半径等来描述不同环境下的原子尺度,它们的尺度通常由测量分子或固体中原子间的距离，然后进行适当的分配而决定.目前 ,尚无简明的理论方法讨论和估算孤立原子的半径[1-4]。

笔者将文献[5]中氢分子共价键键能与结构之间的模型进行了推广，假定碳碳体系键能与结构存在同样的联系.用平均电势能密度守恒[5-9]理论，得出其键长和键能之间的方程式，对碳原子半径进行了计算.理论模型直观，计算方法简单，计算值与实验值高精度吻合。

1 理论模型

将文献[5]中的氢分子成键模型推广到碳碳体系，得到了同样的两条假设：假设 1: 假定两个碳原子形成碳碳体系之后, 碳碳体系的电势能与碳碳体系体积的比值和碳原子的电势能与碳原子体积的比值相等[7]。

假设 2: 碳碳体系的平均电势能与体积的比值和重叠部分电势能与重叠部分体积的比值相等, 也和未重叠部分平均电势能与未重叠部分体积的比值相等[7]。

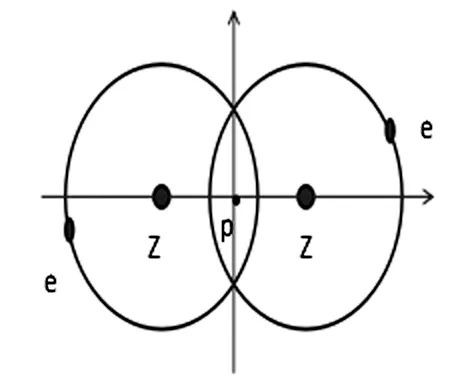
图1 碳碳键结构简图Fig.1 Schematic diagram of carbon and carbon bond

如图1所示，z为碳原子原子核，e为碳原子最外层轨道的电子.将文献[5]中的原子平均电势能密度的定义进行推广，进而可以计算碳原子平均电势能密度的理论方程式，即：

(1)

式中， φc为碳原子的平均电势能密度， 代表碳原子电势能,eV; V代表碳原子体积,m3，k表示静电引力常数，K=8.99×109N·m2/c2；R代表碳原子半径；z表示碳原子的电荷量，其值为6q，e表示最外层轨道的电子电荷量,其值为q，且q值为q=1.60×10-19C。

根据假设，两个碳原子形成碳碳体系之后，其重叠部分的电势能与体积的比值等于未重叠前碳原子的的电势能与体积的比值, 即两个碳原子成键前后平均电势能密度相等[7]。进而可计算碳碳体系重叠部分平均电势能密度：

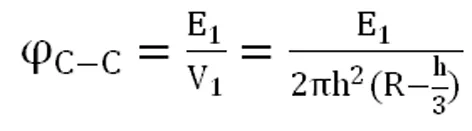
(2)

式中， φc-c为碳碳体系重叠部分平均电势能密度， 表示碳碳体系重叠部分的平均电势能， 表示碳碳体系重叠部分的体积[7]。重叠部分可以看成是由两个球缺组成的，R代表该球体的半径，h代表该球缺的高。

(3)

式中，De表示碳碳键键能，Re表示碳碳体系核间距.

将(1)式、(2)和(3)式联立，根据平均电势能密度守恒，可以得碳碳体系结构与键能之间关系的方程式，即：

(4)

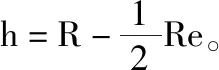
2 碳原子半径计算

对碳碳体系结构和键能的关系进行分析，可以发现该方程式将碳原子半径，碳碳体系键长和键能联系到一起.在已知碳碳体系键长和键能时，可以用来计算碳原子半径.对(4)式进行化简，可以得到碳原子半径的方程式：

(5)

已知，碳碳体系键长为1.54Å，金刚石碳碳键键能为348KJ/mol。用二分法求解该方程组，可以得到碳原子半径的理论计算值为0.907Å。实验值为0.908Å，理论计算值和实验值较高精度吻合，相对误差小于0.1%.

3 结果与讨论：

目前普遍认为宏观理论无法解决原子的激发态、光谱、各种轨道(s、p、d、f)的差异、轨道杂化、π键和共轭键等物质结构中的各种问题[10-14]。然而，笔者将氢分子键能与其结构之间的联系推广到碳碳体系，假定碳碳体系成键的微观机理是两个碳原子转变为碳碳体系后，碳碳体系中重叠部分的平均电势能密度和未重叠前碳原子的平均电势能密度相等[7]。根据碳碳体系结构和键能之间的关系，得到了关于碳原子半径，碳碳体系键长和键能之间的方程式。用二分法求解该方程式，得到碳原子半径的理论计算值为0.907Å ，计算值和实验值较高精度吻合.同时，用该方法对碳原子半径的计算，计算方法极为简单，各物理参数意义明确，且计算过程中不含任何人为定义参数，所得到的计算值和实验值较高精度吻合[8]。这表明一些原子的半径借助宏观方法完全可以较好的解决，暗示原子的空间运动、分子的结构和能量传递仍然可能存在一定新的规律性[8]。