瞬态轴向冲击下固体药柱裂纹动态响应特性探讨

2022-06-06陈晧晖饶永红陈俩兴訾皓然

弹箭与制导学报 2022年2期

方帆，常皓，陈晧晖，饶永红，陈俩兴，訾皓然

(32382部队，北京 100039)

0 引言

固体火箭具有结构紧凑、启动迅速、机动性好等特点，能够长时间保持待命状态，在航天、军事等领域得到广泛应用。然而由复合固体推进剂材料通过贴壁浇注、固化等一系列工艺形成的发动机药柱却对各种外部载荷，如振动、冲击、温度等，非常敏感。譬如，推进剂材料中的氧化剂颗粒多为脆性晶体，在生产过程易产生大量空穴或裂纹缺陷，初始裂纹缺陷可达数十微米。在冲击载荷作用下，上述缺陷极易引发推进剂药柱产生大变形，甚至导致结构破坏，发动机失效。

国内外对于固体推进剂裂纹缺陷扩展和断裂理论开展了大量的研究。Liu利用实验和有限元分析手段，对固体推进剂材料的断裂理论进行了研究，建立并分析了固体推进剂裂纹扩展机理。张淳源从实验的角度，给出了断裂能量与裂纹扩展之间的关系。常新龙等研究了温度对端羟基聚丁二烯复合固体推进剂裂纹扩展特性的影响，研究结果表明，温度越低，裂纹开始扩展的时间越短。袁端才等利用线弹性三维有限元模型模拟了发动机点火时危险部位处裂纹缺陷的扩展，由此判断裂纹的稳定性。职世君等以分子动力学为手段，建立了高填充比固体推进剂细观模型，研究了推进剂颗粒粒径、位置等随机因素对推进剂细观损伤及宏观力学性能的影响。陈广南通过建立微观热点模型，研究了机械冲击对推进剂内部裂纹扩展和点火反映原理，认为在高速冲击下裂纹间摩擦可导致推进剂热点产生。

为了进一步研究裂纹缺陷在轴向冲击载荷下的响应特性，通过建立含有裂纹缺陷的有限元模型，并通过瞬态分析的方法，对药柱在轴向冲击载荷下的动力响应进行了数字模拟。模拟过程考虑了裂纹缺陷的长度、开裂方向等因素对动力响应结果的影响，得出了一系列有用的结论。这一研究过程对于分析、识别和诊断裂纹缺陷具有实际指导意义，同时也为研究复杂结构裂纹缺陷提供了一种有效的方法。

1 裂纹应力场分布关系

在裂纹计算模型中，确定裂纹尖端应力场和应力幅值的方法包括应力强度因子、能量释放率和积分。考虑到积分对线弹性材料和非线性弹塑性材料均适用,因此选取积分作为裂纹前缘应变场的平均度量。

对于二维平面问题，体力作用于积分面内，压力作用于裂纹面内，因而利用域积分表达的积分具有如下形式：

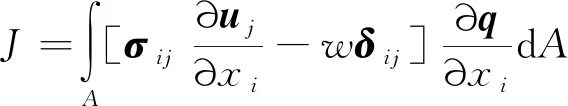
(1)

式中:为应力张量;为位移矢量;为应变能密度;为克罗内克符号;为坐标轴;为裂纹扩展向量。

积分的守恒性质能够使积分在计算过程中有效地避开复杂的裂纹前缘应力场，离开尖端处完成应力场、位移场的计算，非常适合于有限元方法。结合单元离散化，可以给出积分如下离散表达形式:

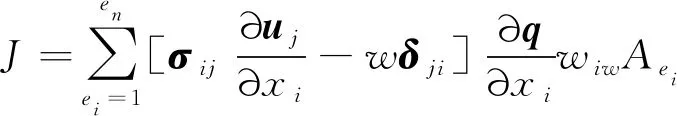
(2)

其中：为域积分涉及单元数量;为权值。

2 计算模型

在轴向冲击载荷条件下，为了研究裂纹故障对发动机药柱动力特性的影响，选取某型固体火箭发动机药柱作为研究对象进行建模。该发动机药柱为贴壁浇注的内侧壁燃烧式单孔管状药柱，剖面如图1所示。

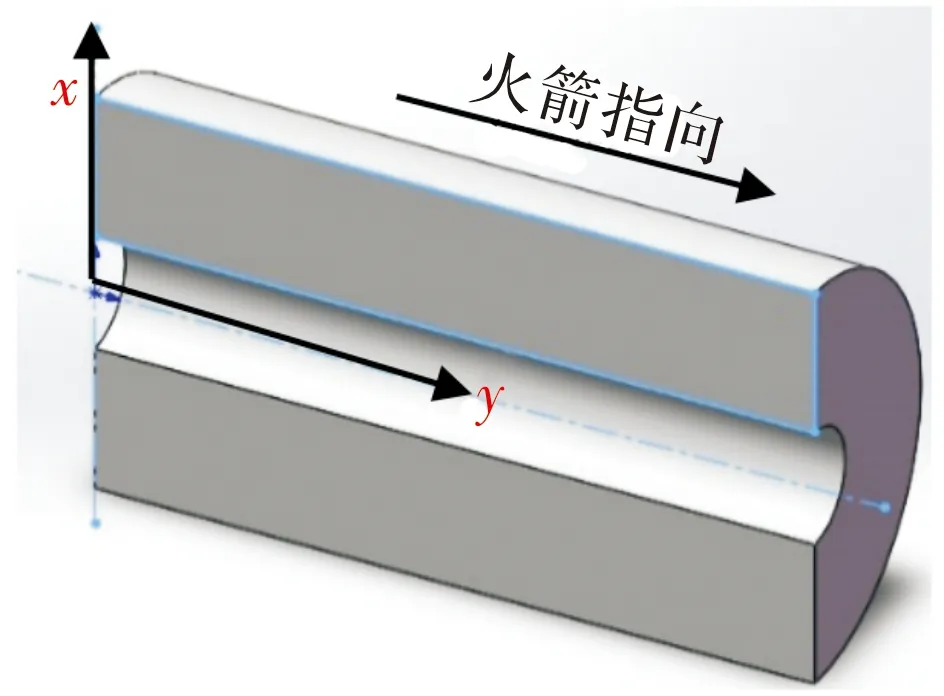
图1 固体发动机药柱剖面图

为了方便对比分析，建立了两类火箭发动机药柱的计算模型，分别为无故障药柱模型和有裂纹缺陷药柱模型。其中，有裂纹缺陷药柱模型又按照裂纹长度和开裂方向分为两类，每一类型缺陷各设置2种算例以便对比研究。

2.1 假设条件

贴壁浇注的固体火箭发动机药柱动力响应分析，虽属三维应力-应变分析问题，但是由于药柱的长径比一般比较大，可以按照广义平面应变问题进行处理。为进一步简化分析过程的计算量，对药柱模型进行了如下假设：

1)根据载荷和药柱结构的对称特性，选取药柱截面的二分之一进行建模，在对称面上均采用对称约束以保证模型不失实际约束状态；

2)忽略药柱自身由于加工工艺所产生的倒角、圆角等结构；

3)忽略绝热层、人工脱粘层，将药柱与壳体固结连接。

2.2 材料性能

固体火箭推进剂是粘弹性物质，具有近似不可压缩特性。在计算中，药柱材料的松弛模量采用Prony级数的形式表达为：

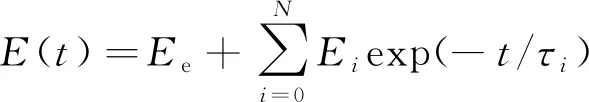
(3)

式中：平衡模量=1.535 MPa;为松弛时间;为松弛系数。和参数取值如表1所示。

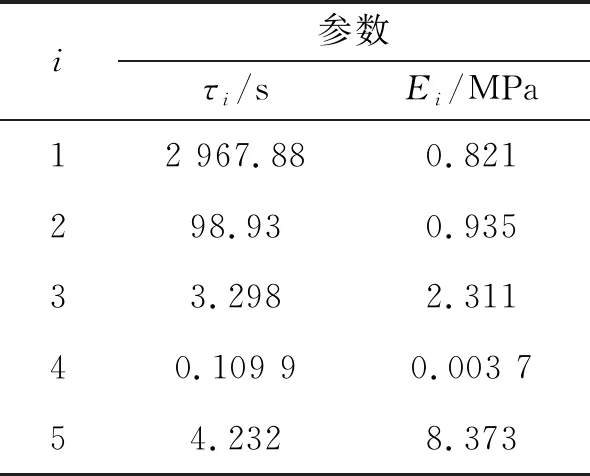
表1 药柱材料参数列表

药柱材料的密度为1 730 kg/m，泊松比为0.495。

2.3 物理模型及有限元网格

药柱半径=35 mm，壁厚=60 mm，轴向长度=120 mm，裂纹位置=35 mm，裂纹长度为，裂纹开裂角度为，如图2所示。4种故障模型的裂纹尺寸分别设置为：1)=4 mm，=0°；2)=8 mm，=0°；3)=4 mm，=-45°；4)=4 mm，=45°。选取火箭指向为坐标系正方向，药柱顶端、外壁与发动机壳体接触区域处理为完全约束。

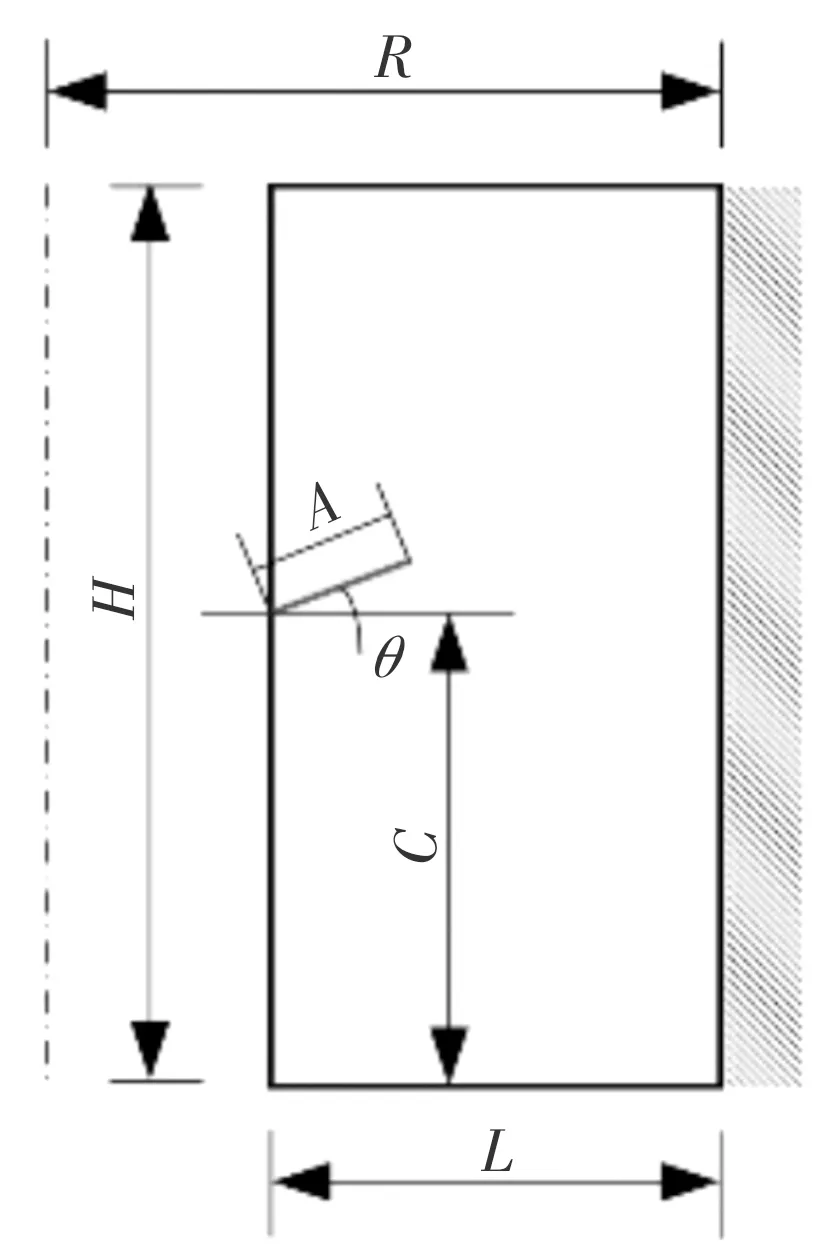
图2 具有裂纹缺陷药柱剖面视图

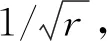
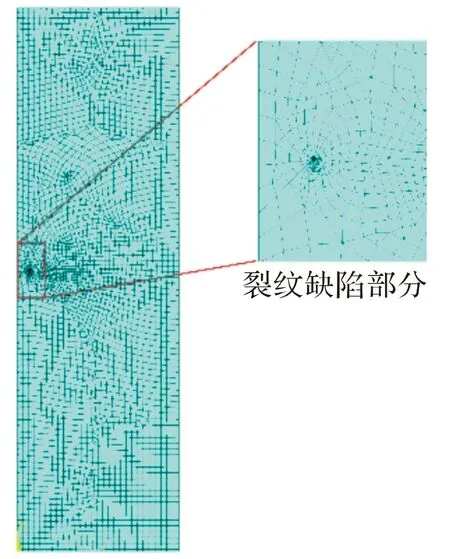
图3 药柱有限元模型

3 轴向冲击载荷工况

发动机工作中轴向冲击载荷是一种常见载荷。在二级火箭起飞、级间分离等过程都会受到轴向冲击。以文献[11]提供的火箭级间分离载荷数据为参考，选取该载荷作为研究药柱裂纹动态响应的载荷工况，并建立轴向冲击载荷的推力如式(4)所示：

(4)

为了详细说明轴向冲击的随时间的变化，对上述推力公式进行如下表述：级间分离过程所产生的轴向冲击包括推力上升、推力恒定、推力撤销等3个阶段，虽然推力上升过程几乎为非线性过程，但是为了便于载荷输入，将上升过程处理为线性加载过程。

4 裂纹对药柱动态响应的影响分析

4.1 裂纹长度对动态响应的影响

利用有限元软件ANSYS对上述四种具有裂纹缺陷的药柱进行了瞬态响应分析，同时与无裂纹缺陷药柱模型的瞬态响应进行对比。无裂纹缺陷药柱瞬态响应如图4所示，其中图4(a)～图4(d)分别为取0.2 s,0.5 s,1.0 s,1.7 s时刻的位移分布图。由仿真结果可以看出，药柱最大应变为2.56 mm，主要发生于药柱中后部，与壳体固结部分变形量较小。另外，由于药柱刚度小，存在明显的迟滞特性，冲击波在药柱内传播速度较壳体要慢，因此，药柱形变最大时刻发生于推力撤销阶段。

图4 无裂纹缺陷药柱位移分布图

图5为第1种裂纹缺陷药柱位移分布，其中，图5(a)～图5(d)分别为取0.2 s，0.5 s，1.0 s，1.7 s时刻的位移分布图。与图4对比可以看出，初始阶段=0～0.5 s时的应变基本相同。随着时间历程的演进，冲击波传递到药柱裂纹处，并发生了明显的应力集中现象，对比图4(c)与图5(c)产生了明显的位移形变。图5(d)进一步显示裂纹缺陷区域普遍具有较大的位移形变，相对无裂纹缺陷状态要高15%～30%。

图5 第1种裂纹缺陷药柱位移分布图

进一步增大裂纹的长度，可以得到如图6所示的位移分布图。其中，图6(a)～6图(d)分别为取0.2 s，0.5 s，1.0 s，1.7 s时刻的位移分布图。由图6(d)可以看出，裂纹长度的增加引起了缺陷区域非常明显的位移突变，相对无裂纹缺陷状态要高60%以上，对裂纹附近药柱形态影响较大，很容易使药柱局部受到损伤和破坏，冲击环境较恶劣。

图6 第2种裂纹缺陷药柱位移分布图

4.2 开裂方向对动态响应的影响

由理论分析可知，不同的裂纹开裂方向对药柱完整性的影响也不同。图7和图8分别为第3、第4种裂纹缺陷药柱位移分布，其中，图7(a)～图7(d),图8(a)～图8(d)分别为取0.2 s，0.5 s，1.0 s，1.7 s时刻的位移分布图。

图7 第3种裂纹缺陷药柱位移分布图

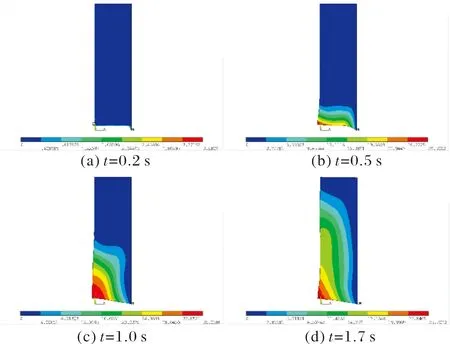
图8 第4种裂纹缺陷药柱位移分布图

通过与图6(d)的仿真结果对比可以看出，图7(d)裂纹缺陷处发生1.7 mm以上位移的区域相对较小，说明，该裂纹走向对冲击波传播影响较小，有利于冲击能量的扩散。由图8(d)的仿真结果进一步看出，由于裂纹开裂方向与冲击波传播方向一致，对能量扩散的影响更小。因此，即使第种裂纹与第种裂纹的长度相同，但是对药柱位移分布产生的影响要小很多，对药柱完整性所带来的影响也更小。

裂纹长度越长、开裂方向越接近药柱表面法向，裂纹对药柱的影响也越大，越容易发生局部突变，需要在后续设计中予以充分考虑。