基于KICA改进算法的运动目标检测
2019-09-12宣峰
宣 峰
(浙江交通职业技术学院,杭州 311112)
0 引 言
运动目标检测是计算机视觉学科、图像处理领域的重要分支,一直以来都是该领域的研究重点。运动目标检测是指把感兴趣的前景和背景从视频或图像序列中进行分离。而目前主要有三种较流行的检测算法应用于运动目标的检测:背景相减法[1]、帧差法[2]和光流法[3]。背景相减法比较常用,其基本思路是建立和不断更新背景模型,通过比较待检测图像帧与背景模型的符合程度实现运动目标检测。当待检测像素点(或块)与背景模型的差异小于设定阈值,则该像素点(或块)被判定为背景;否则被判为运动目标。这种阈值函数比较方法基于绝对误差准则,并没有考虑背景像素的具体取值变化,势必将影响运动目标的实际检测精度。帧差法的局限在于运动目标速度不能过快,否则单一目标会被检测为多个目标。而光流法由于需要计算视频图像中每个像素点的运动信息,计算复杂度过高,实时性不好。
而在目标检测过程中,会因为多光源引起的光照和运动目标遮挡部分背景的等问题,导致运动目标和背景之间必然会存在相关性,这势必会影响到运动目标的分离效果。独立分量分析(ICA)[4]是一种新兴的盲源分离算法,目的就是将待检测的图像数据进行线性分解,将其分解成为统计独立的分量,求解分离矩阵则是建立目标函数和寻优逼近的过程。ICA算法通过线性解混模型,希望得到的背景和运动目标具有独立性。但是运动目标与背景并不是完全统计独立的分量。文献[5]将核方法与KICA进行结合,应用于运动目标检测,在线性加权和阈值判决基础之上,考虑由于遮挡和光照等因素所引起的非线性,通过非线性特征映射在无穷维的重建核希尔伯特空间(RKHS)中,进行最小最大典型相关性分析确定线性加权系数。KICA通过利用核方法,并非在原始特征空间讨论解混后的背景和运动目标的关系,而是利用特征经过高维映射后,原来的非线性问题可能会变为线性这一特性,在高维特征空间讨论分离分量的第一典型相关性。但运动目标提取时,KICA沿袭了ICA的线性解混模型,等于是用一个线性模型来逼近非线性问题,这是它的局限性所在。故无论是ICA还是KICA都是在线性模型基础上进行阈值判决从而得到运动目标,并没有充分考虑其中的非线性因素。因此,提出改进的KICA算法,在线性模型的基础上,加入了二阶加权矩阵,使得线性模型变成了非线性模型,借此希望用非线性模型来解决非线性问题,这无疑比线性模型解决非线性问题的角度,更具有优势。
1 基于核方法的独立向量分析算法(KICA)
1.1 核方法
核方法的核心思想是将通过在低维空间中线性不可分的模式,经过非线性映射到高维特征空间中,则可能会变成线性可分的模式。但是如果在高维空间直接进行数据分类或回归,会存在确定非线性映射函数的具体形式、参数以及特征空间维数等问题,而且在高维空间运算会存在的“维数灾难”问题会增加计算复杂度。使用了核方法,可以解决上述问题。
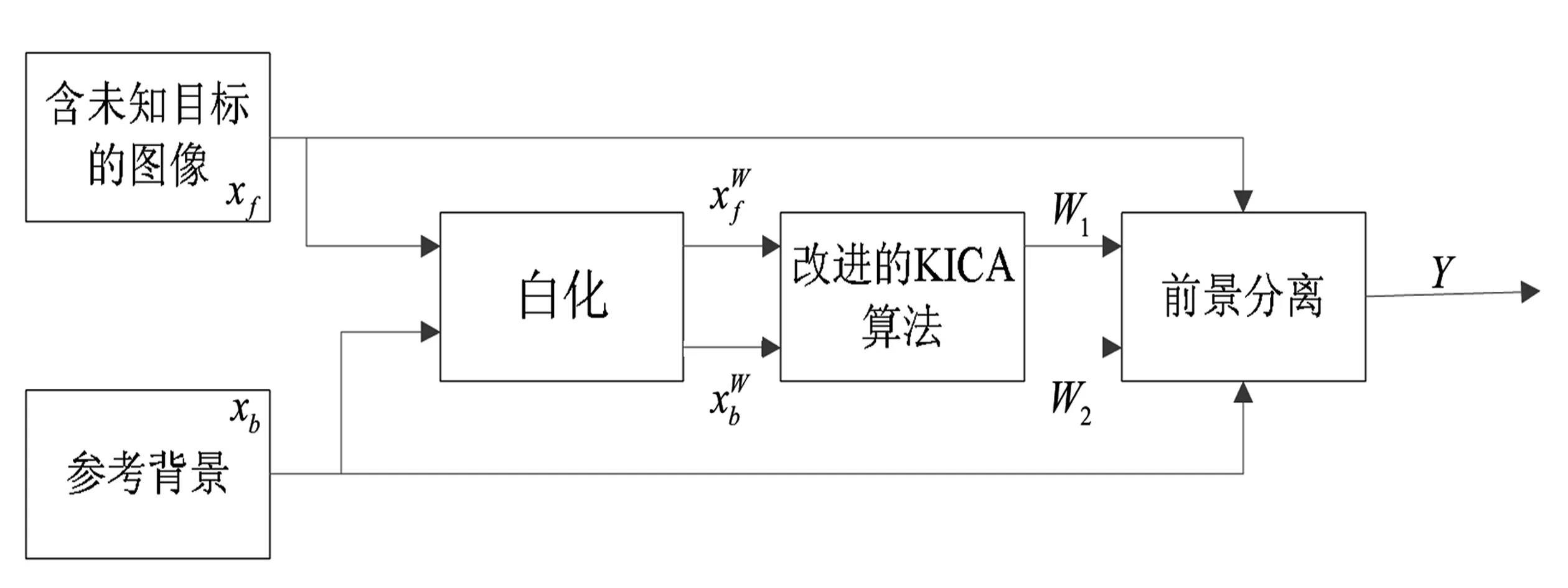
设x,y∈X,X属于Rn,非线性映射函数Φ表示低维输入空间X到高维特征空间F的映射,其中F属于Rm,n< K(x,y)=〈Φ(x),Φ(y)〉 (1) 从式(1)可以看出,核函数通过在m维高维空间进行内积运算后,高维空间的运算问题被转化成了n维低维空间的核函数运算,规避了高维空间映射所引起的“维数灾难”等问题。核函数虽然表达了非线性映射函数Φ,但计算过程中并不需要明确Φ的形式和参数,且通过改变核函数类型和相应的参数可以改变Φ,影响映射关系,从而影响特征空间的产生,最终影响各种核函数方法在应用时的表现。 常见的核函数有下列几种: 线性核函数:K(x,y)=xTy 多项式核函数:K(x,y)=(1+xTy)d 径向基核函数(RBF): Sigmoid函数:K(x,y)=tanh((xTy)+C) 对常见核函数进行重构,可得到新的核函数,称之为重构核函数。近期的研究[6]表明,使用多个不同的核函数进行重构,比单一核函数有时性能更优。 线性核重构,见式(2): (2) 其中,M是需要组合核函数的个数,σm是需要学习的权重。根据具体情况来确定目标函数,权重的学习需要根据具体类型数据进行性能测试来选择。或对核集合中任意两个或几个核进行Hadamard求积来做非线性核重构,以此生成新的核函数,在此基础上线性核重构,最终得到最优核。 除了线性核函数重构,也可用非线性方式进行核函数重构。以下函数为非线性核重构,见式(3)~(5): K(x,y)=K1(x,y)K2(x,y) (3) K(x,y)=eK1(x,y) (4) (5) 以上都是较常用的核函数,无论是单一核,还是重构核,不同的核函数在解决不同的问题上各具有优劣。 KICA是建立在ICA的基础之上的,采用了ICA的基本模型。 对于静态定焦摄像机的视频图像序列,每一帧图像可以看作是运动目标和背景的混合。每一帧图像可以按行排列成一个N维的列向量,其中N=m×n(m,n分别代表图像长宽的像素点)。对于m×n的视频图像,两帧已知的背景和含前景图像分别用列向量表示xb=[xb1,xb2,…,xbk]T和xf=[xf1,xf2,…,xfk]T,其中K=m×n。根据线性ICA可以表示为式(6): X=AS (6) 其中,X=[xb,xf]T已知;S=[s1,s2]T是未知的源图像分量,包含了真实背景向量s1=[sb1,sb2,…,sbN]T和真实的运动目标向量s1=[sf1,sf2,…,sfN]T;A是未知的2×2混合系数矩阵。ICA的目标就在未知前后景和混合矩阵的情况下,使得Y的分量尽可能独立,那么Y的分量就是前后景的最佳估计,如式(7): Y=[y1,y2]T=WX=W[xb,xf]T (7) 其中,W=[w1,w2]T是2×2的解混矩阵,W=A-1。独立图像分量y1和y2可以作为s1和s2的估计。 在实际中,由于遮挡和光照等因素,式(7)应该是非线性的,且无法得到的。因此,引入二阶加权矩阵来逼近S的估计值,如式(8): Y=W1X+W2X* (8) 其中,W1是线性部分的加权矩阵;W2是非线性部分的加权矩阵,大小为2×4;X*=[xb⊗xb,xb⊗xf,xf⊗xb,xf⊗xf]T,⊗表示克罗内克积。 算法的整体流程如图1所示。 图1 算法的流程框图 在使用改进的KICA算法进行运动目标检测之前,要对观测数据进行中心化和白化预处理。如果一个零均值向量,它的各元素不具备相关性且具有单位方差,则称该向量是白化的。白化预处理能够避免尺度的不确定性和一定程度上去除信号间的相关性,降低数据计算复杂度。 中心化处理可使数据的均值为零,可表示为式(9): (9) 数据的白化方式如式(10): (10) 经过白化之后,式(8)变为式(11): Y=W1XW+W2XW* (11) 第一典型相关系数定义如式(12): (12) 其中,C11=(K1+Nk/2·I)2,C22=(K2+Nk/2·I)2,k是正规化估计子。 (13) 求解式(12)也等价于求解以下问题,如式(14): (14) 由式(14)进行变换可得式(15): (15) 又因为λF和ρF为正数,可得λF=1-ρF。 这里定义经验比对函数为式(16): (16) 由于上述的变换关系,C(W1,W2)表现了第一典型相关性。 (17) 这里,首先更新W1,W2值不变,直到W1收敛;然后更新W2,W1值不变,直到W2收敛。重复上述过程,直到到达循环次数或者W1,W2都收敛。 为了验证算法的有效性和可靠性,使用室内场景下的一段视频,大小320×240,帧速为每秒10帧,该场景下的背景和前景被室内灯光、室外自然光同时影响。不同时刻,室外日照差异及室内开灯情况,营造一个光线变换的场景,用于检验在灯光强度变化、受室外光影响的室内环境下算法检测前景目标的性能。选取的参考背景,与含未知运动目标的图像具有明显的光照差异。 目前KICA算法参数选择没有统一定论。虽然,组合核性能可能会优于普通的核,但不绝对优于,而且参数选择的难度会较单核更大。为了比较KICA与KICA改进算法的优劣性,选用综合性能较优的高斯核, 在核方法中高斯核具有两个参数:正规化系数k和核宽度σ2。当σ2趋向0时,Gram矩阵K的每个元素趋向于1;当σ2趋向无穷大时,Gram矩阵K的每个元素趋向于0。以上两种极端的情况均会影响KICA的对比函数,使其不能很好地逼近相关系数,从而影响情景分离的性能。另一方面,k需要根据信号长度N的大小和Gram矩阵选择一个合适的值。 在实际应用中,一般会分别使用正检率(R)、检出率(P)、F测度(F)和相似度(S)四种检测性能指标来对不同参数的性能差异进行衡量,比较不同算法的实验结果。通过这四个参数性能来选取较优的高斯核。正检率等于检测结果中属于目标的像素点数与检测结果全部像素点数的比值;检出率等于检测结果中属于目标的像素点数与目标像素点的总数的比值,P越高表示检测结果中正确像素数越多;F测度和相似度作为补充,F或S越大分别表示误检率和漏检率低。四种性能指标按式(18)进行计算: (18) 其中:tp是检测结果中属于目标的像素点数;fn是检测结果中不属于目标的错误像素点数;fp代表属于未检测出目标部分的像素点数。 表1 参数对分离的影响(l=1.5) 根据表1中R、F和S的参数,可以看出随着k的减少,正确检测到目标点的数目在增加,且检测性能在变好;由P可以看出,KICA几乎能将所有检测点检测出来。而核宽度对检测性能的影响,当k比较小时,随着σ2的增大,正确检测到目标点的数目先增加再减少,相似度也是如此,可看出σ2存在极值,能使KICA的性能优化。综上可得,不在影响运算速度的情况下,k应该选尽可能小,而对于σ2,需要找到其极值,才能最优化KICA算法。这里最优选择是,k=0.002,σ2=0.25。 用KICA改进算法得到运动目标图像后,需要使用一个自适应门限来二值化图像,以方便与其他算法的比较。 二值化门限设置,采用自适应门限,如式(19): thres=m0+l·var0 (19) 其中:m0为输入图像像素均值;var0为方差;l根据情况设定,默认为1.5。 实验中选取的参考背景图像与含前景图像是从摄像机视频的不同时间点提取的,可以明显看到,室外光存在明显的强弱差异,由于运动目标遮挡了来自室外的部分强光,室内的光线也存在着强弱的差异。故由于光线和运动目标遮挡的关系,选取的含前景图像与参考背景图像明显存在着一定相关性问题待解决。 KICA和KICA改进算法的前景分离效果图,如图2所示。 (a)参考背景图像 (b)含前景图像 (c)KICA算法检测到的二值化前景图 (d)KICA改进算法检测到的二值化前景图 图2KICA和KICA改进算法的前景分离效果图 从图2的前景分离效果图可以看到,通过改进后的KICA算法提取的运动目标的性能比KICA算法的好。这取决于在KICA改进算法中,在原有线性的前后景分离模型中加入了二阶加权矩阵,从非线性的角度来解决非线性问题。 在运动目标检测过程中,由于运动目标图像与背景图像之间存在的相关性使得KICA算法的检测依然存在着缺陷。KICA虽然考虑到将数据从低维映射到高维特征空间中,利用了非线性问题在高维空间可能会转化为线性问题这一特性,并且采用典型相关分析来优化KICA的经验对比度函数,但是在分离前景与背景的这一过程中,依然沿用了ICA的线性模型,并没有从本质上解决光线以及遮挡带来的非线性问题。KICA改进算法在KICA的基础上,改进了分离前景与背景的线性模型,通过引入二阶加权矩阵,把线性模型转变成了非线性模型,从本质上能更好解决问题。通过实验证实了KICA改进算法拥有更优的目标检测性能。1.2 KICA原理
2 改进的KICA算法及实现
2.1 预处理
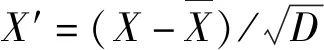

2.2 算法实现
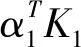
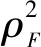
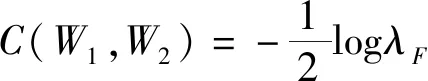


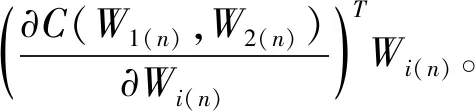
3 算法仿真与性能分析
3.1 算法参数选择

3.2 KICA算法与KICA改进算法的仿真结果


4 结 语
