高精度Stewart平台运动控制系统设计*

武锡铜, 周 烽, 王 永

(中国科学技术大学 信息科学技术学院，安徽 合肥 230026)

0 引 言

大型望远镜光路系统通常包括主镜、次镜，为了保证良好的成像质量，需要主镜与次镜的反射面焦点重合，光轴重合。然而由于重力、振动等原因，主镜和次镜之间的位姿往往会发生改变，从而导致望远镜成像质量受到影响，因此需要对主次镜之间的位姿进行精确的调整和校正。由于主镜的尺寸、质量远大于次镜，若对主镜进行调整，其功耗较大，实际工程中往往采用次镜调整机构来调整主次镜之间的相对位姿[1]。

而Stewart平台因其高精度、高刚度的优点，在大型望远镜中作为次镜调整机构被广泛使用[2]。本文所研究的Stewart平台控制系统，作为次镜调整机构，控制任务为控制动平台从当前位姿点运动到目标位姿点，要求运动过程平稳且不超过工作空间，并且能够快速无差的稳定到目标位姿。

1 Stewart平台运动学模型及其反解

1.1 Stewart平台运动学模型

本文Stewart平台为6—UCU构型，由上平台、下平台及6条支腿构成，其中上平台为动平台，下平台为静平台。上下平台与6条支腿之间通过虎克铰相连，支腿运动机构可简化为移动—转动副，通过控制6条支腿的长度变化，可控制上平台的3个方向的平移和3个方向的旋转。

平台简化模型和坐标系如图1(a)所示，动坐标系P-X'Y'Z'与静坐标系O-XYZ分别固定在上下平台中，P和O点分别为上下平台的中心点。Stewart平台上下平台的铰链中心点分别记为A1A2A3A4A5A6和B1B2B3B4B5B6，外接圆半径分别为r，R，分布角分别为θ，φ，其具体分布如图1(b)所示。

图1 Stewart平台简化模型及铰链中心分布

1.2 Stewart平台位置反解

已知上平台和下平台之间的位姿关系，求解对应的各支腿长度，被称为Stewart平台的位置反解(此处位置的含义为广义位置)。位置反解是对Stewart平台进行运动控制的基础[3]。上平台和下平台之间的位姿关系描述可分为位置和姿态两部分，记位姿向量u=[xyzαβγ]T，其中,[xyz]T为P点在静坐标系O-XYZ中位置向量，α,β,γ分别为ZYX欧拉角中绕Z轴、绕Y轴、绕X轴旋转角。记Ai(i=1,2,…,6)在动坐标系P-X'Y'Z'中的位置向量为OAi，Bi(i=1,2,…,6)在静坐标系O-XYZ中的位置向量为OBi，则各支腿长度为

Li=‖li‖2=‖R·PAi+P-OBi‖2,i=1,2,…,6

(1)

式中R为旋转角分别为α,β,γ时的旋转矩阵。

2 工作空间轨迹规划

由于并联平台特殊的闭环运动链构型，其工作空间有限[4]，若让各支腿直接运动到运动学反解计算出的目标位置处，在运动的过程中动平台可能会超出工作空间,因而必须对并联平台进行轨迹规划。考虑动平台从位姿点u1到位姿点u2的轨迹规划，由于所设计控制系统只需实现点位控制，对轨迹形状不做要求，为求简便，取轨迹为6维空间内的一条线段。同时为使运动更加平稳，使用梯形速度曲线对平台运动速度进行规划。

按平台能否加速到最大速度分为两种情况，如图2所示。

1)能够加速到最大速度时，速度和加速度曲线如图2(a)所示，0～t1段为加速段，以amax做均加速运动；t1～t2段为匀速段，以vmax做匀速运动；t2～t3段为减速段，以-amax做匀减速运动，此时α(t)可计算为

(2)

2)不能加速到最大速度时，速度和加速度曲线如图2(b)所示，0-t4段为加速段，以amax做均加速运动，此时α(t)可计算为

(3)

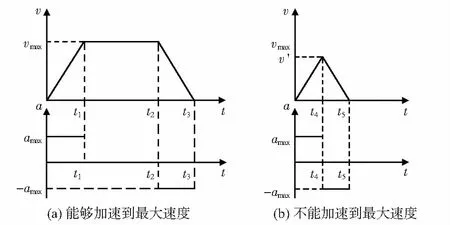
图2 两种情况下速度和加速度曲线

3 关节空间建模与辨识

在对实际系统缺乏了解时，直接进行控制器设计往往存在风险和不便。因此，在控制器设计之前，首先通过辨识的手段，得到关节空间的信息，即支腿的模型信息。关节空间的控制任务为控制支腿跟踪由工作空间规划轨迹反解得到的位置曲线，由于支腿位置可看作是运动速度的积分，本节将对支腿的速度—电压关系进行建模和辨识。

关节空间中，由直流电机驱动滚珠丝杆带动支腿上部运动，使支腿长度发生改变。不考虑负载力的影响，可将支腿的速度—电压开环传递函数近似为[5]

(4)

式中U(s)为输入电压，Y(s)为输出速度，Te为电磁时间常数，Tm为机械时间常数，K为等效放大系数。

为得到式(4)中参数的具体数值，使用频率响应法对支腿进行辨识，其思想为测量系统在不同频率正弦信号输入的输出响应，以求得系统模型的待定参数[5]。

对关节空间进行辨识实验，以不同频率的幅值A为6 V的正弦信号作为系统输入

u(t)=Asin(ωit)

(5)

式中ωi=2iπ,i=1,2,…,10。设置采样周期为1 ms，则h=0.001 s，对每个测试频率，运行6 s，并记录其中2～4 s的速度值，进行多次实验，将相同时间点处的速度值取平均值，求得各频率点幅值放大倍数和相移角度如表1所示。

表1 各频率点对应的幅值放大倍数和相移角度

各个频率点的Me，φe分别得到对应的z为

z=Me[cos(φe)+jsin(φe)]

(6)

将频率特性向量z=[z1z2…z10]T，角频率向量ω=[ω1ω2…ω10]T，开环传递函数分子阶数nb=0,分母阶数na=2，代入invfreqs(z,ω,nb,na)中，得到关节空间开环传递函数的估计为

(7)

绘制出实际系统传递函数与辨识得到传递函数的频率特性曲线，如图3所示。

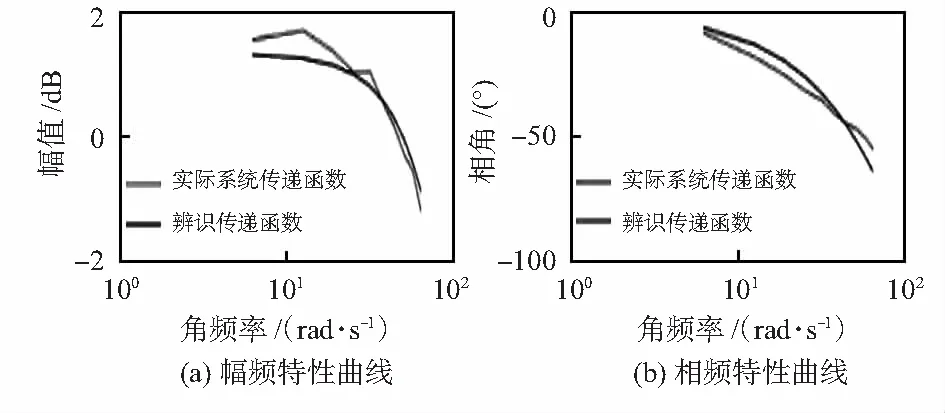
图3 实际系统和辨识得到传递函数的频率特性曲线

由图3可以看出，使用频率响应法能够较好地辨识出关节空间的支腿速度—电压开环传递函数，这一模型信息将会被用于关节空间的控制器设计中。

4 关节空间控制器设计

在高精度位置控制器设计中，往往采用位置—速度双环控制方案。其中，速度内环控制的主要目的是抑制外部扰动，增强鲁棒性。通常希望通过内环控制器的校正作用，使得校正后的内环特性尽可能的接近名义模型，这样在外环控制器设计时，即可将名义模型视为实际的控制对象[6]。

已通过辨识实验得到关节空间的速度—电压模型，但由于未建模部分和外部扰动的影响，其和真实系统之间必然存在差距。考虑所建立模型和实际对象的差别，将关节空间的速度—电压关系用微分方程表示

(8)

式中f'为实际系统未建模部分和外界扰动的总体作用，视为总扰动，由式(7)可知a0=9 232，a1=169.25，b=10760。

x=Ax+Bu+E',y=Cx

(9)

构造模型辅助的扩张线性状态观测器

z=(A-LC)z+[BL]uc,yc=z

(10)

式中uc=[uy]T为组合输入，yc=[z1z2z3]T为组合输出，z1为对x1的估计，z2为对x2的估计，z3为对f'的估计，L=[l1l2l3]T为参数需要设计的观测器增益矩阵。

为使z→x，观测器特征方程的根应均具有负实部，为求简便，将其均配置在-ω0处，即

λ(s)=|sI-(A-LC)|=(s+ω0)3

(11)

则有

(12)

则模型辅助的扩张状态观测器为

(13)

选取合适的观测器带宽ω0，即可保证z→x，从而得到系统各状态和总扰动的估计。取式(14)中控制律

u=kp(r-z1)-kdz2-(z3-a1z2-a0z1)

(14)

又有z→x，则闭环系统为

(15)

则输出y和输入参考信号r之间的闭环传递函数为

(16)

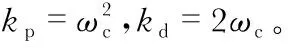
对位置外环设计比例—积分控制器，控制律为

(17)

式中err为位置环参考信号r'与当前位置y'之差，errI为位置误差的积分。为加快镇定速度，在最后稳定阶段引入积分重置策略，即当检测到当前位置超过目标位置时，直接将errI重置为0，从而减小支腿运动超调的距离。

5 实际控制系统与实验

Stewart平台控制系统的总体框架如图4所示。

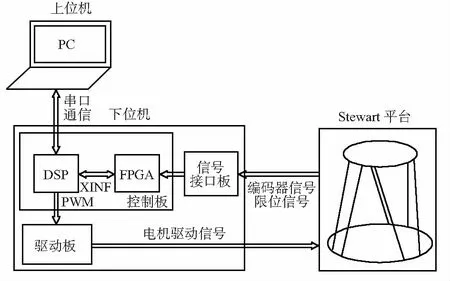
图4 高精度Stewart平台控制系统总体框架

实际控制系统由上位机、下位机、Stewart平台组成。采用FPGA+DSP异构方案，FPGA和DSP通过外部存储器接口通信，实现传感器信息(增量式编码器、限位开关)的读取和控制信号(PWM信号)的产生[8，9]。接口板实现差分转单端、电平变换、光耦隔离等功能。驱动板由6对PWM信号控制，驱动平台按照给定轨迹运动。

为验证所设计控制系统性能，进行Stewart平台运动控制实验。平台具体尺寸为r=90 mm，R=148 mm，θ=110.078 6°，φ=15.7965°。控制周期为1 ms，限制平台位姿的位置分量的最大速度和最大加速度幅值为1 mm/s和1 mm/s2，姿态分量的最大速度和最大加速度幅值为1°/s和1°/s2。

控制Stewart平台从中位点[0 0 244.827 3 0 0 0]T运动到[4 -1 247.827 3 3 -1 -1]T处，记录0～20 s各时刻的支腿长度，并利用高斯—牛顿法求得对应的动平台位姿，绘制出位姿变化曲线如图5所示。

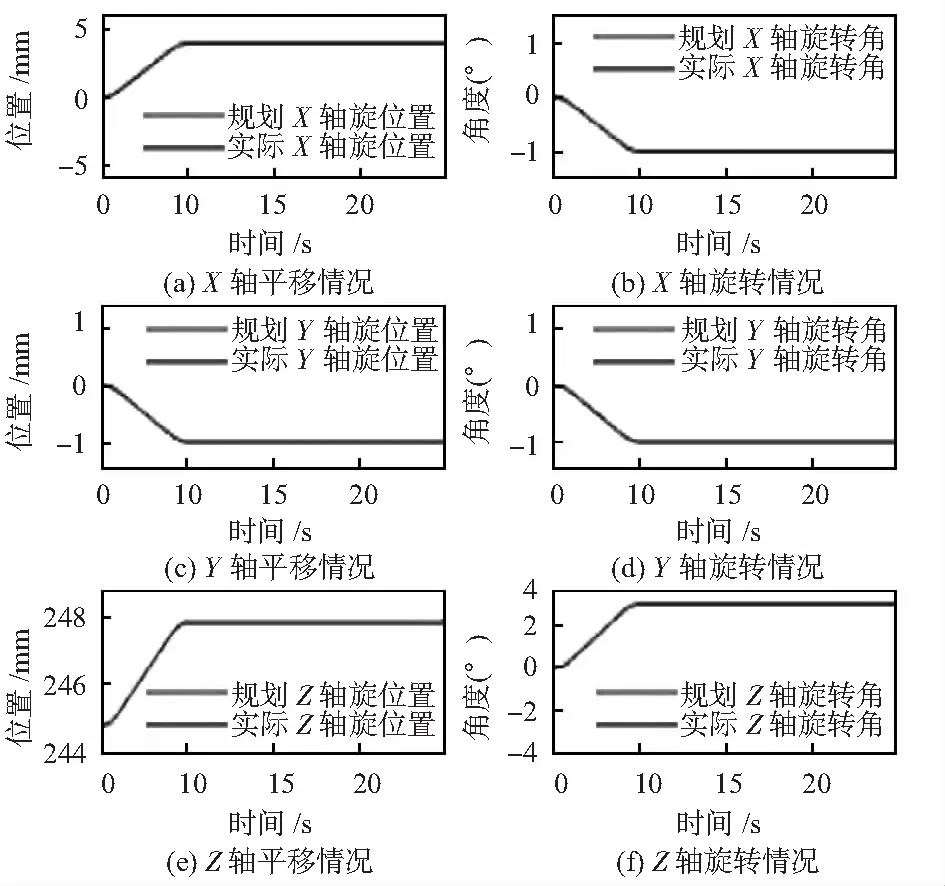
图5 平台运动时位姿变化曲线

从图5中可以看出，动平台按照所规划的轨迹运动，运行平稳，且在开始运动和停止运动时均有妥善的过渡过程。其在0～5 s的轨迹跟踪阶段，平台位置跟踪误差在0.01 mm以下，姿态角跟踪误差在0.005°以下，并且在5.8 s左右，动平台位姿镇定。最终平台稳定在[3.999 89 -0.999 90 247.827 17 2.999 92 -1.000 01 -1.000 02]T，偏差与位置传感器量化误差在一量级，因而可以将其忽略，认为平台已经稳定在给定位姿上。

6 结 论

实验结果表明：在本文所设计的控制系统控制下，高精度Stewart平台运行平稳，具有良好的跟踪精度，并且最终能够较快的稳定到目标位姿，取得了理想的控制效果。