一种抑制NLOS误差的UWB定位方法*
2019-09-11鲍小雨程向红
鲍小雨,王 庆,阳 媛,程向红
(东南大学 仪器科学与工程学院,江苏 南京 210096)
0 引 言
基于超宽带(ultra-wide band,UWB)的定位技术具有多径分辨能力强、抗干扰性强、定位精度高等优点,随着设备成本的降低,UWB定位技术逐步成为性价较高的一种定位方法[1]。由于UWB信号时间分辨率可高达纳秒(ns)级,因此,UWB定位系统常用基于时间的方法获得基站与标签之间的距离,然后利用距离信息对标签进行定位[2],但往往会受到多径效应、非视距(non-line of sight,NLOS)误差的影响[3]。
在室内定位的应用场景中,测距精度对定位精度有很大的影响。为了提高定位精度,提高测距精度和研究定位算法至关重要。Garcia E等人[4]提出了基于估计的信道脉冲响应的偏度的NLOS检测算法并使用扩展卡尔曼滤波来减轻NLOS传播引起的正偏差。贾俊超[5]提出一种卡尔曼滤波增益自适应的滤波方法,并基于几何关系推导出一种定位算法。文献[6]提出了一种基于误差先验知识引导的NLOS移动节点定位算法,在降低定位误差的同时降低了计算复杂度。王长强等人[7,8]提出用一种偏移卡尔曼滤波的方法结合测距残差和卡尔曼滤波实现实时抑制NLOS误差,提高NLOS环境下的定位精度。文献[9]将误差归化为虚拟延时,得到关于虚拟延时因子、终端位置参数的欠定方程组,该方法在平面上可达到厘米(cm)级的定位精度。
本文设计了一种改进的扩展卡尔曼滤波(improved extended Kalman filtering,IEKF)算法,首先对UWB设备进行标定实现对测距信息的修正,然后在普通扩展卡尔曼滤波(extended Kalman filtering,EKF)的基础上进行改进,以修正后的测距值作为滤波器的观测值;并增加NLOS误差判别环节,设定阈值区分LOS数据与NLOS数据,调整滤波增益,抑制NLOS误差,提高定位精度。
1 UWB定位系统
图1为UWB定位系统的标准架构,由4个锚(anchor)基站、1个标签(tag)、路由器和服务器组成[10]。Tag和Anchor之间进行通信,测量两者间的距离[11]。

图1 UWB定位原理
实际环境中,测得的Tag和Anchor间的距离可表示为
di=ri+ei
(1)
式中di为Tag与Anchor距离测量值,ri为真实值,ei为标准偏差。
为了获得精确的测距值,本文对UWB模块进行标定,即对测距数据进行一次线性拟合,并利用拟合优度判定系数来判断拟合优劣
(2)
式中R2定义为拟合优度的判定系数,yj为实际数据,Yj为拟合数据。R2分布在区间(0,1),R2越小,拟合得越差;R2越大,拟合得越好。
当Tag与Anchor间存在障碍物干扰时,测得的距离会变大[12],从而使得定位精度明显下降。因此非常有必要对NLOS误差进行判别与剔除,从而提高定位精度,得到稳定可靠的定位服务。
2 IEKF算法
EKF对非线性系统局部线性化,适用于弱非线性系统[13,14]。本文所提出的IEKF定位算法,以标定后的UWB测距数据作为IEKF的观测数据,设定阈值进行NLOS判别并调整滤波增益,剔除受NLOS影响的数据,抑制其对定位精度的不良影响。
2.1 状态方程
算法的状态向量为Tag的运动状态,即
Xk=[xkykkk]T
(3)
式中xk和yk为Tag的位置;k和k为矢量速度。
状态方程为
Xk+1=FXk+ωk
(4)
(5)
式中F为状态转移矩阵;Tc为采样时间;Q为过程噪声协方差;q为过程噪声的功率谱密度。
2.2 观测方程
在二维平面内,UWB的Anchor与Tag之间的距离为
(6)
式中N为Anchor的个数;di为第i个Anchor与Tag的距离;(xi,yi)为第i个Anchor的坐标,是已知量;(x,y)为Tag的坐标,是待求量。
系统的观测向量为Tag与各Anchor之间的距离,即
Zk=[d1d2…dN]T
(7)
由式(6)可知,观测向量Zk与状态向量Xk为非线性关系,将观测方程局部线性化,可简化为
Zk=HXk+υk
(8)
(9)
式中υk为第k个采样的观测噪声,通常假设为加性的并且对角自相关的矩阵R。
2.3 算法流程
根据状态方程和观测方程,通过EKF进行状态更新及观测更新,即
(10)
式(10)为状态的一步预测与均方误差的一步预测方程。
由于在室内环境下,行走的人员、障碍物都会对UWB信号造成遮挡,带来NLOS误差,因此本文对EKF稍加改进,将实际观测值与状态向量的预测值进行比较,再将二者的差值与阈值相比。若差值小于等于阈值,可认为数据是LOS场景下的,滤波增益不作改变;若差值大于阈值,表明该组数据存在NLOS误差,将增益设置为0,则有
(11)
(12)
式中thresh为事先选定的阈值。最后,对状态和均方误差进行更新
(13)
2.4 误差判定标准
为了对定位精度进行定量分析、便于比较经典EKF算法与IEKF算法的定位精度,对定位误差定义为
(14)

3 实验与实验结果
实验使用的UWB模块为南京沃旭公司的WxRobot机器人定位产品,由UM208(Tag)和4个UK—100(Anchor)组成。
3.1 UWB测距标定
实验在李文正北楼一楼大厅内进行,可保证实验过程中Tag和Anchor之间无障碍物遮挡、无人员走动,完全为LOS场景。首先用Anchor1(A1)进行实验:A1固定不动,Tag从0.5 m移动至6.5 m,步长为0.5 m,共计13个测距点;在每个点处获取上百个测距数据,先用3σ准则剔除粗大误差,再对剩余数据取平均值,用作该测距点的测量距离;最后与真实距离进行一次线性拟合,获得基站的标准偏差的误差模型,完成基站的标定。其余Anchor用同样的方法进行处理,以供后续定位实验测距数据预处理使用。
表1为4个基站的拟合函数的相关参数,并用式(2)计算拟合优度。根据拟合优度的定义,可以看出一次线性拟合提供了接近完美的拟合结果。

表1 基站标定参数
3.2 UWB定位实验
为了验证本文提出的IEKF算法对NLOS误差有抑制作用,分别进行了静态实验和动态实验,并将IEKF的结果与经典EKF的定位结果进行对比。实验在李文正北楼一楼大厅内进行,场地大小为5 m×9 m;获取实验数据过程中,人员不停走动或短暂停留引入NLOS误差。
3.2.1 UWB静态实验
UWB静态定位实验是指Tag静止不动,对其进行定位。实验布置如图2所示,五角星(A1~A4)代表Anchor,三角形(P1~P8)为静态实验测试点;先后将Tag置于P1~P8位置,获取其与基站的测距数据,分别用EKF算法以及IEKF算法进行定位解算,利用式(14)计算定位误差,比较定位精度。该实验中,设定NLOS判定阈值为15 cm。

图2 实验布置
表2列出了静态定位的两种算法结果的误差统计,以P5为例,观测环境较好时,两种算法的精度相当;当存在NLOS误差时,EKF误差为33 cm,IEKF误差仅有8 cm。整体来看,本文IEKF算法能在NLOS环境下有效准确地进行定位,定位精度较EKF提高约7 %。
3.2.2 UWB动态实验
实验布置如图2所示,动态实验中行走路径:从P2出发,沿P1,P4,P5,P8,P7运动(5字型)。该实验中,设定NLOS判定阈值为65 cm。
图3为EKF和IEKF的定位结果。表3列出了两种算法定位结果的误差统计。

表2 测试点定位误差比较 cm
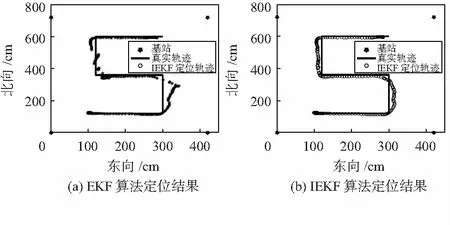
图3 二种算法定位结果

EKF最大值最小值平均值 IEKF最大值最小值平均值44.120.118.6616.150.306.88
图3(a)中,利用经典EKF对NLOS/LOS混合场景下移动的Tag进行定位,结果表明,观测环境良好时,EKF算法解算结果可以很好地贴近真实路径;存在NLOS误差时,定位误差较大,高达44 cm,甚至定位轨迹出现断点。在图3(b)中,利用本文提出的IEKF算法进行定位,定位结果明显优于图3(a),最大误差仅有16 cm且未出现定位断点。整体来看,IEKF算法定位精度较EKF提高了约20 %,且定位连续性更佳。
4 结束语
UWB定位系统中亟待解决的问题是测距标准偏差和NLOS误差对定位精度的不利影响,针对前者,本文进行测距实验,利用一次线性拟合求解测距数据中的标准偏差,进而对设备进行标定;针对后者,本文提出了一种改进的EKF算法,以修正后的测距值作为滤波器的观测数据,设定阈值判别LOS数据与NLOS数据,调整滤波增益,剔除NLOS误差。实验结果表明:视距环境下,静态定位和动态定位精度均可高达5 cm;非视距环境下,静态定位精度为9 cm,动态定位精度为20 cm。本文所提出的方法能大幅提高定位精度,适用于LOS/NLOS混合环境的定位。
