例析“等时圆”在物理中的妙用

叶向忠

摘 要：物理学科的中心素养，是学生在承受物理教育过程中逐步形成的顺应个人毕生发展和社会发展需求的必备品格和关键能力，是学生通过物理学习内化的带有物理学科特性的品质，是学生科学素养的关键成分。其中“科学思维”是提升物理核心素养的重要一环，而物理建模、物理思维是发展科学思维的一大捷径，因而想更直观、简约地解决物理问题，常把复杂的实际问题转化并抽象成简单地“物理模型”，在分析和解决物理问题时，一般都是在已经把握的“物理模型”的启发下找到解决物理问题的思绪与方法。所以在平时的教学过程中加强“物理模型”的建立与应用是至关重要的，这也是提升学生物理学习力、培养学生物理核心素养的重要渠道。本文就以“等时圆”这一物理模型的建立与在物理中的应用来阐明如何帮助学生建构物理模型，并加以拓展、转化应用，发展科学思维。

关键词：物理模型;等时圆;建模;应用

物理模型是对实践成果的抽象，每一个模型的建立都有必然的条件和实用领域，在学习和运用物理模型解决物理问题时，最重要的一个环节是把实际问题简化成相应的物理模型，借助由根本物理规律所构建成的一些基本物理模型，可以把抽象问题具体化，把复杂问题简单化，从而使物理问题便于理解和接受，化难为易，化繁为简，达到意想不到的效果。下面就以“等时圆”模型为例，体会如何通过巧妙地构建物理模型达到简化求解，基于此对“等时圆”的规律和应用从三方面加以阐述：分别是动力学中的“等时圆”，磁场中的“等时圆”及光学中的“等时圆”。

动力学中的“等时圆”

模型建立

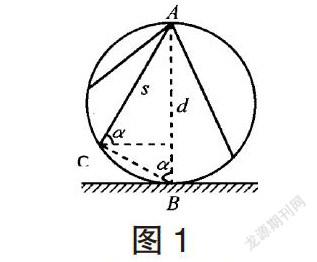
如图1所示，A为竖直平面内圆周的顶点，AB为竖直直径，质点从A点静止释放，沿着不同的光滑弦到达圆周上的时间相等，此圆称为“等时圆”，该圆就是重力场中的“等时圆”

证明：设某一条弦AC与水平方向的夹角为α，圆的直径为d（如图1）。根据物体沿光滑弦作初速度为零的匀加速直线运动，加速度为a=gsinα，位移为s=dsinα，所以运动时间为

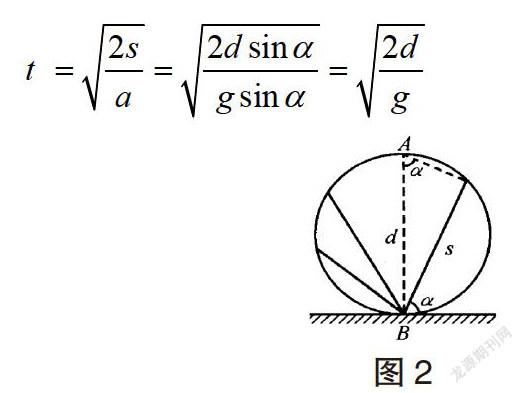
显然t与α无关，即从A点沿不同的光滑弦到达圆周上的时间相等，且等于从最高点A自由下落到B点的时间，这个叫做圆的自由弦的等时性，即沿各条弦运动具有等时性，运动时间与弦的倾角、长短无关。同理，如图2所示情形，从圆周上不同的点沿光滑弦滑到圆周上的最低点B，所需的时间也相等（证法同上），需要说明的是，等时圆中的端点应是几何空间的最高点或最低点。

模型适用条件

“等时圆”的适用条件是：在重力场的竖直平面内任意的一个圆上，质点从几何最高点（或圆周上）沿任何一条弦无摩擦下滑到圆周上（或几何最低点）发生的时间相等。

模型应用

借助“等时圆”模型，可以使抽象问题具体化，复杂问题简单化，方便于学生理解和接受。利用“等时圆”模型可以巧妙、方便地解决相关问题，它常用于以下几种情况。

能直接观察到的等时圆

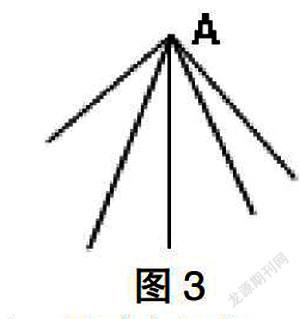
例1：如图3所示，通过空间任一点A可作无限多个斜面，若将若干个小物体从点A分别沿这些倾角各不相同的光滑斜面同时滑下，那么在同一时刻这些小物体所在位置所构成的面是（ ）

A.球面 B.抛物面 C.水平面 D.无法确定

解析：由“等时圆”可知，同一时刻这些小物体应在同一“等时圆”上，所以A正确。

确定运动路径

有些问题我们不能直接观察出来，有时需要运用等效、类比来构建“等时圆”。

例2：如图7，AB是一倾角为θ的输送带，P处为原料输入口，为避免粉尘飞扬，在P与AB输送带间建立一管道（假设光滑），使原料从P处以最短的时间到达输送带上，则管道与竖直方向的夹角应为多大？

解析：常规的解法就是利用解析法进行求解：设P点到斜面的垂直距离为PC，P点与传送带的位置确定后，PC就是一个定值，原料沿最快管道PD下滑的加速度为a=gcosβ，有：

在ΔPDC中，有，则

由数学知识可知，当时，t有最小值

若借助“等时圆”，如图4所示，可以过P点的竖直线为半径作圆，要求该圆与输送带AB相切，如图所示，C为切点，O为圆心。显然，沿着PC弦建立管道，原料从P处到达C点处的时间与沿其他弦到达“等时圆”的圆周上所用时间相等。因而，要使原料从P处到达输送带上所用时间最短，需沿着PC建立管道。由几何关系得：PC与竖直方向间的夹角等于θ/2。

比较以上两种解法，可以看到利用“等时圆”解题要比解析法来的直观、简洁、快速。

3、比较运动快慢（计算运动时间）

例3：两光滑斜面的高度都为h，OC、OD两斜面的总长度都为l，只是OD斜面由两部分组成，如图8所示，将甲、乙两个相同的小球从斜面的顶端同时由静止释放，不计拐角处的能量损失，问哪一个球先到达斜面底端？

解析：（解法1）本题采用v-t图象求解，作出物体分别沿OC、OD斜面运动的v-t图象（如图9），由图可得乙球先到达斜面底端。

解法2：构建如图10所示的等时圆，交OC于A点，交OD于B点。由“等时圆”可知，tOB=tOA，由机械能守恒定律可知，VB>VA，VC=VD，所以VBD>VAC，又因为两斜面的总长度相等，故XBD<XAC，所以有tBD<tAC，有t乙<t甲，即乙球先到达斜面底端。

解后反思：对于涉及竖直面上物体运动快慢、运动时间的比较、计算等问题，可考虑用“等时圆”模型来求解，会更直观、高效，激发学生的思维，提升建模的能力，给学生带来意想不到的效果。

磁场中的“等时圆”

模型建立

如图11所示，在xoy平面内有垂直于xoy平面的匀强磁场，坐标原点O处有一粒子源，在某时刻发射出大量同种带电粒子，它们的速度大小相等，方向均在xoy平面内，与y轴的正方向的夹角分布在0--3600的范围内。则在任一时刻这些粒子都在同一个圆上，此圓称为磁场中的“等时圆”。

证明：设带电粒子的质量为m（不计重力），电量为q，速度为v，匀强磁场的磁感应强度为B，那么带电粒子在洛伦兹力的作用下作匀速圆周运动，运动轨迹如图11实线所示：

经过时间t，任一粒子到圆心O点的距离均为：，将所有粒子所在位置用一曲线连接起来，这就是我们所说的“等时圆”，如图11虚线所示。

应用例析

例4：如右下图所示，在0≤x≤a，0≤y≤a/2范围内有垂直于xy平面向外的匀强磁场，磁感应强度大小为B。坐标原点O处有一个粒子源，在某时刻发射大量质量为m、电荷量为q的带正电粒子，它们的速度大小相同，速度方向均在xy平面内，与y轴正方向的夹角分布在0～90°范围内。求最后离开磁场的粒子从粒子源射出时的。

（1）速度的大小;

（2）速度方向与y轴正方向夹角的正弦。

分析：本题的难度是：学生分析不出最后离开磁场的粒子究竟是哪一个粒子，其运动轨迹有什么特征？如果运用“等时圆”模型就能迅速化解此难点。

解析：画出三个半径相等且满足的“抽样”轨迹圆，如图19实线所示，让带电粒子分别从矩形匀强磁场的上边界、右边界、下边界的三个不同段射出，每个“抽样”轨迹圆与边界的交点即为带电粒子出磁场的点，以右边界上的出射点为圆周上的一点，O为圆心，画出一个“等时圆”，如图12虚线所示;同理，以与磁场的上边界相切的出射点为圆周上的一点，O为圆心，画出一个“等时圆”，如图13虚线所示;由此可以轻松的判断出：运动轨迹与磁场上边界相切的粒子在磁场中的运动时间最长。

解析：设粒子的发射速度为v，粒子做圆周运动的轨道半径为R，粒子在磁场中的运动时间为t，根据洛伦兹力提供向心力：有：

如图14所示：依据题意，有，∠OCA=900，由几何关系可得： 得：，则有：

3、评析：

学生在求解本题时，难点是不能找到问题的突破口，也就不能分析得出结论：在磁场中运动时间最长的粒子，其轨迹与磁场的上边界相切，运用“等时圆”模型能清晰找到此临界情况，从而克服难点。

光学中的“等时圆”

1、模型建立

如图15，一束平行光经平面界面折射后仍为平行光，对入射光束作垂直平面AB，这是入射光的一个波面;对折射光束作垂直平面A′B′，这是折射光的一个波面.那么各光线从一个波面传播到另一个波面所经历的时间是否相等？

分析：由折射定律可得：

设光束边缘的两条光线在两个波面间传播的距离分别为x1，x2，所以有：

，可得即：t1=t2

结论：当一束平行光发生折射时，各光线从一个波面传播到另一个波面的时间相等。这是单色光的等时性，对于单色光的直线传播及反射也同样成立。那对于复色光呢？有怎样的结论？

如图16所示，一束白光PO从真空斜射入某种介质中，入射点为O，发生折射后，各种单射光在相同的时间内从入射点开始到达的位置均在一个几何圆周上，此圆称为“等时圆”。

证明：在O点的右侧介质界面上任取一点N，作以ON为直径的半圆。设白光折射色散后的边界红光为OH，紫光为OZ，（H，Z为圆周上的交点）;作过N点与入射光线PO平行的光线MN（白光），又过端点O作平行光MN的垂线OM交MN于M点，根据惠更斯原理可知，对于介质中的红光OH的H点（或紫光OZ的Z点）与N点处于同一波面上，即白光在真空中从M点传播到N点的时间等于在介质中红光从O点传播到H点（紫光从O点传播到Z点）的时间。各种色光在真空中的波速是相等的，所以不论是红、紫光还是其他的单色光，在介质中色散彼此传播的光线均是一簇发散弦，光线在这些弦上传播时间均相等。这就是光学中的“等时圆”。

2、应用例析

如果我们能够借助于惠更斯的“等时圆”模型，求解有关光的传播时间问题，便很能清晰地说明问题，直观易懂，加深印象，更有利于学生理解与掌握。

例5：如图17所示一束由红、蓝两单色光组成的光线从一平板玻璃砖的上表面以入射角θ射入，穿过玻璃砖从下表面射出，已知该玻璃对红光的折射率为1.5，设红光与蓝光穿过玻璃砖所需时间分别为t1和t2，则在θ逐渐由0°增大到90°的过程中有：

A. t1始终大于t2 B. t1始终小于t2

C. t1先大于后小于t2 D. t1先小于后大于t2

解析：（解法1）设折射角为α，玻璃砖的厚度为h，由折射定律，且，在玻璃砖中的时间为：，联立解得

红光频率较小，θ为零时，t1

此法定量去解析求解，比较繁琐，不直观易懂，且需要特殊值代入加以检验，说服力不强，若能够借助于惠更斯的“等时圆”模型来求解，则简洁、直观，问题就迎刃而解。

解法2：已知该玻璃对红光的折射率为1.5，则临界角的正弦值为，而，即红光的临界角小于450，那么紫光的临界角也小于450，也就是最大的折射角都小于450，由图18可知，构建一个惠更斯“等时圆”，在折射角小于450的情况下，在等时圆中蓝光对应的等时弦始终小于红光的等时弦，所以在平行玻璃砖中，折射率小的折射光线在其中的距离总比原来在等时圆中等时弦短，则对应的时间就短，所以在在平行玻璃砖中红光传播的时间始终小于蓝光传播的时间。

若玻璃对红光的折射率为1.4，则临界角的正弦值为，表明临界角大于450，因此当入射角增大到一定值时，折射角会大于450，此时等时弦如图19所示，对于平行玻璃磚，折射率大的折射光线在其中的距离比原来在等时圆中等时弦短，则对应的时间就短，因此，在折射角逐步从零增大的过程中，红光在平行玻璃砖传播的时间先小于蓝光传播的时间，而后大于蓝光传播的时间。

结语：核心素养，是每个人发展与完善自我、融入社会及胜任工作所必需的基础性素养，是适应个人终生发展和社会发展所需要的必备品格与关键能力。科学的基本活动就是探索与建立模型，帮助学生从新的物理情境中提取有效信息，挖掘隐含条件，构建物理模型，然后把所学的物理概念和规律迁移到问题中快速找到解决问题的方法。面对这样一群鲜活的、有学习积极性的学生，我们教师应该针对性地进行这方面的训练，以提高思维的敏捷性和建模能力，从而助推物理核心素养的提升。

参考文献

[1]《中国学生发展核心素养》文件.2016年

[2]黄国龙《高中物理竞赛重要思维方法专题》浙江大学出版社2018年

[3]范小辉《新编高中物理奥赛指导》南京师范大学出版社2017年

[4]郑志湖、郑陆敏《“学为中心”的高中物理教学》浙江教育出版社2017年