移相全桥变换器软开关设计及效率优化

黄伟 罗文广 黄丹

摘   要： 针对负载减小时传统移相全桥变换器滞后桥臂的开关管实现软开关的范围变窄，变换器效率降低的问题，通过分析变换器的工作过程以及变换器超前滞后桥臂实现软开关的条件，研究谐振电感取值不同对占空比丢失、滞后桥臂实现软开关、变换器效率的影响;设计移相全桥变换器电路参数，并通过saber软件进行仿真.结果表明取适当的谐振电感值，增加滞后桥臂软开关范围，可以优化变换器效率.

关键词：移相全桥变换器;软开关;效率优化;滞后桥臂;谐振电感

中图分类号：TM46      DOI：10.16375/j.cnki.cn45-1395/t.2019.03.008

引言

电力电子变换器不仅要满足高效率、高功率密度、高可靠性等电气性能指标，还要有较低的成本、较小的体积、较轻的质量、较低散热要求、较高适应环境能力等优点[1-3].由于变换器的输出功率与开关管的个数成正比，所以全桥变换器的功率最大，广泛应用于高输入电压及中大功率场合中.

随着软开关技术出现，硬开关的不足得到解决.软开关是指通过控制脉冲使开关管两端电压为零时导通（零电压导通 ZVS）或使流经开关管电流为零时关断（零电流关断 ZCS）.软开关技术，在开关管开通、中断瞬间，电压电流变化无交叉点，实现理想的开关损耗为零，同时减小电磁干扰，得到广泛应用[4].零电压开关PWM全桥变换器[5]，大大减小了开关损耗，有利于减小变换器体积和重量，有助于提高开关频率，进而较好的满足高效率、高功率密度、高可靠性且成本低的性能要求.但零电压开关PWM移相全桥变换器随着负载逐渐减小，滞后桥臂的开关管实现ZVS的范围变窄，轻则导致开关管发热，效率降低[6-7]，重则导致变换器无法正常工作.针对这个问题，本文在参数设计上进行研究，增加变换器滞后桥臂软开关范围，优化变换器的效率.

1    移相控制ZVS PWM全桥变换器的工作分析

移相全桥变换器有3种控制方式[8]，工作原理本质一样，现以移相控制为例，分析其工作原理与软开关实现的条件.图1为主电路拓扑，其中Q1-Q4为开关管，D1-D4为二极管，C1-C4为寄生电容，L1为谐振电感，Dr1与Dr2为副边稳压二极管，Lf与Cr起滤波作用.图2为主要波形图，其中t0到t2时段内相位差为移相角，移相角越小，输出电压越高，反之越小.假设：电路中的电容、电感、开关管、二极管、变压器都是理想元器件;且 C2 =C4，C1=C3; Lf[≫] Lr/K ，K为变压器原副边匝数比.在一个开关周期内，共有12个开关模态，由于前后6个周期的原理相同，因此只分析前6个模态的原理.

开关模态0：如图3所示，t0时刻前，开关管Q1、Q4导通，电流从电源正极流出，经过开关管Q1、变压器原边绕组、谐振电感L1、开关管Q4最后回到负极.变压器副边回路从副边绕组顶端到整流二极管Dr1、输出滤波电感Lf、电容Cf与负载，再回到副边绕组形成回路.

开关模态1：如图4所示，在[t0，t1]时段中，t0时刻，C1充电，C3放电.在此期间，副边电流因为滤波电感Lf的作用保持方向不变，原边电流受其影响方向不会发生改变，D1导通将Q1两端电压箝位至0，使得Q1零电压关断.t1时刻，C3电压下降到0，D3导通.

开关模态2：如图5所示，在[t1，t2]时段中，D3导通后，将开关管两端的电压箝位至0，此时无电流流经Q3，实现Q3零电压开通.电流i为原边滤波电感电流.

开关模态3：如图6所示，在[t2，t3]时段内，t2时刻，Q4零电压关断，C3放电，C4充电，VAB极性发生变化，变压器副边绕组电势为上负下正，整流二极管Dr2导通，此时Dr1与Dr2都导通，副边绕组电压为0.相应的，原边绕组也为0，此时VAB作用在谐振电感L1.t3时刻，C4电压上升到Vin，D2导通.

开关模态4：如图7所示，在[t3，t4]时段内，D2导通，将Q2两端电压箝位为0，Q2开通，但此时无电流流经Q2，实现Q2零电压开通，谐振电感L1将存储能量反馈电源.此时原边绕组电压依旧为0，电源电压Vin全部加在谐振电感L1两端，电流i线性递减[9].t4时刻，电流减小到0，D2、D3关断，电流流经Q2、Q3.

开关模态5：如图8，在[t4，t5]时段内，t4时刻，电流流经Q2、Q3，电流由0反向增加，但还未到提供负载电流的程度.t5时刻，原边电流达到原边负载电流，整流管Dr1关断，Dr2流过全部负载电流[10].

开关模态6：如图9，在[t5，t6]时段内，电源给负载供电.t6时刻，Q3关断，之后变换器进入下半个工作周期.

在[t2，t5]时段内，原边电流极性发生变化，由正变负的过程中，由于谐振电感，原边电流不足以提供负载电流，副边整流管全部处于导通状态，输出滤波电感电流处于续流状态[11]，整流输出后的电压为0，所以副边丢失部分占空比.

2 软开关分析和设计

从以上分析可知，移相全桥实现零电压导通软开关（ZVS），必须要有足够的能量使开关管并联的寄生电容进行充放电，并联二极管顺利导通，将开关管两端的电壓箝位至0.而提供这能量的主要是电感.同时，超前桥臂和滞后桥臂实现软开关又有所不同.超前桥臂在实现ZVS中，其能量来源于滤波电感Lf与谐振电感L1.滤波电感Lf在超前桥臂开关过程中类似恒流源，能量充足，超前桥臂易实现ZVS.因为变压器副边短路，只有谐振电感L1提供能量来实现滞后桥臂的ZVS，所以在负载减小时滞后桥臂难实现ZVS.

移相全桥电路要实现超前桥臂的ZVS，必须满足死区时间大于寄生电容放完电之后，二极管在开关管导通之前，将电压箝位至0，则有：

式中，Ci——超前桥臂的寄生电容，Cr——滞后桥臂的寄生电容，L1——谐振电感，Vin——输入电压，I——原边电流.

滞后桥臂实现ZVS主要受L1的影响，只有L1的能量大于C2、C4充放电所需的能量，才能实现滞后桥臂的ZVS，因此有：

式中，I1为流过谐振电感的电流.

由式（1）可知：开关管并联的寄生电容Ci越小，超前桥臂越容易实现ZVS.输入电压Vin为固定值，从 式（3）可知：原边电流I1 越大，滞后桥臂越容易实现ZVS.原边电流受负载影响，负载减小时，原边电流I1减小，[I21]减小的更为严重，只有大幅度的增加L1的取值，滞后桥臂才能实现ZVS.则L1越大，越利于滞后桥臂实现软开关，但随着L1的不断增大，副边占空比的丢失就越来越严重[12-14]，导致输出功率的降低，影响变换器效率的降低.但另一方面，受到式（2）的限制，L1Cr太小不利于超前桥臂实现软开关，即使占空比的丢失减小了，如果不能实现软开关，会增加开关损耗，也会降低变换器的效率.

为了保证移相全桥变换器滞后桥臂能够实现软开关，效率最大化，当谐振电感的能量恰好全部消耗在实现软开关过程中，就不会影响之后变压器原边的输出功率，可得：

如果负载发生变化：当负载变小时，原边砺磁电流Im变小，谐振电感的能量不足以提供电容充放电，无法实现软开关，开关损耗增加，变换器效率下降.负载变大时，原边电流变大，谐振电感的能量远大于电容充放电的能量，多余的能量会使电流不能即刻下降到0，即电流方向会保持上一状态的流动方向，会消耗原边的能量降低变压器原边的输出能量，效率下降.因此，根据式（4）计算出来的谐振电感值有利于增加变换器滞后桥臂软开关范围，减小开关损耗，获得较优化的效率.

3 参数设计及仿真分析

3.1   参数设计

电路主要元件参数：输入电压Vin=80 V，输出电压10 V，输出电流10 A，功率100 W，变压器原副边匝数比K=5，取超前桥臂的寄生电容为3 nF，滞后桥臂的寄生电容为1 nF，由式（1）和式（2）可计算出：

[tdead=0.64 μs]，[tdead<1.33 μs]

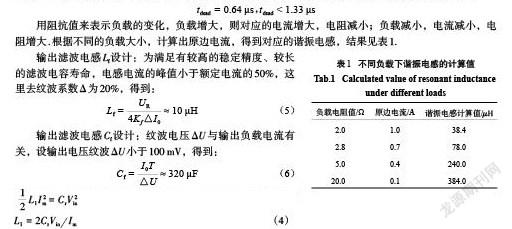
用阻抗值来表示负载的变化，负载增大，则对应的电流增大，电阻减小;负载减小，电流减小，电阻增大.根据不同的负载大小，计算出原边电流，得到对应的谐振电感，结果见表1.

输出滤波电感Lf设计：为满足有较高的稳定精度、较长的滤波电容寿命，电感电流的峰值小于额定电流的50%，这里去纹波系数[Δ]为20%，得到：

输出滤波电感Cf设计：纹波电压[ΔU]与输出负载电流有关，设输出电压纹波[ΔU]小于100 mV，得到：

实际应用中选取的电容要远大于理论计算值，这里取Cf=350 [μ]F，T为一个周期的时间.

3.2   基于saber软件仿真分析

saber软件对电路的分析功能强大，主要有直流分析、瞬态分析、频域分析、傅里叶和快速傅里叶分析及蒙特卡洛等，适用于电力电子、机械、光学等各种不同领域组成的混合系统仿真，仿真描述能力精致、真实性高.

基于saber软件搭建仿真电路图如图10所示，仿真结果如图11—图14所示.

图11给出了滞后桥臂上、下开关管实现软开关的情况.由图11可以看出，当开关管的触发电压Vgs下降为0之后，开关管两端的电压Vds才开始增加，两者没有交集，实现了零电压开关.

图12为不同谐振电感取值下，移相全桥变换器副边占空比丢失情况.由图12可知，随着谐振电感取值的不断增大，副边占空比丢失越严重.

图13为不同谐振电感值在负载变化时，变换器的开关损耗变化情况.由图13可以看出，随着负载电阻值的增大，开关损耗也增加.电感值增大，开关损耗减小.当L1=384 μH时，整个负载电阻值区间内开关损耗几乎为0，由此可以推出在全区间内，变换器都实现了软开关.L1=38.4 μH时，在负载电阻增加到2 Ω之后，开关损耗增加，软开关实现变得困难.由图13可知，谐振电感取值越小，变换器实现软开关的范围就越窄.

图14为不同谐振电感值在负载变化时，变换器的效率曲线图.由图14可知，谐振电感值越小，负载电阻越小时，变换器效率越大.结合图13和图14可以看出：当谐振电感L1=38.4 μH、78 μH、240 μH，负载电阻分别在2.0 Ω、2.8 Ω、5.0 Ω时开关损耗刚好降为零，是实现软开关的临界点，变换器的效率最高.其中，谐振电感为38.4 μH时效率达到最高81.7%，240 μH时只有55.0%，但软开关范围大.因此，谐振电感设计时，需要在滞后桥臂的软开关范围与变换器效率之间做取舍.应考虑较大负载时的原边电流来计算，适当地增加滞后桥臂的软开关范围，优化变换器效率.

4 结论

移相全桥变换器滞后桥臂实现软开关会影响变换器的效率.如果谐振电感取值过大，能够轻易实现滞后桥臂软开关，但会导致占空比丢失严重，降低输出功率，从而导致系统效率下降.如果谐振电感取值过小，当负载减小时，滞后桥臂上的开关管就难以实现软开关，带来不可忽略的开关损耗，影响系统效率.由此可以得出结论：

1）隨着谐振电感的增加，变换器滞后桥臂的软开关范围变宽，但占空比丢失变的更为严重，系统效率整体下降.

2）随着负载变化，变换器的效率存在着最大值，其最大值受谐振电感的影响.谐振电感增大，效率最大值随着负载减小的方向移动.

3）当负载很小时，变换器效率低，谐振电感值对效率影响低.当负载很大时，变换器效率高，谐振电感取值对效率影响大;电感值过大，降低的变换器效率远大于开关管损耗降低的效率，电感值太小开关管又难以实现软开关.在设计谐振电感时，应考虑较大负载的情况来计算，适当的增加滞后桥臂的软开关范围，降低占空比丢失，获得一个较优化的变换器效率.

参考文献

[1]     邓开元. 大功率移相全桥同步整流电源关键技术的研究[D].北京：北京交通大学，2017.

[2]     尹强，熊泽成，朱子庚，等. 移相全桥ZVS PWM变换器的研究[J].电力电子技术，2018，52（1）：11-12，32.

[3]     刘胜永，唐安琼. 一种新颖的软开关双向DC/DC 变换器分析与设计[J]. 电力自动化设备，2012，32（3）：28-31.

[4]     王建秋. 一种基于移相全桥软开关技术的开关电源的研制[D].大连：大连交通大学，2010.

[5]     黄海宏，王海欣，张毅，等. PWM整流电路的原理分析[J].电气电子教学学报，2007，29（4）：28-30，33.

[6]     朱栋. 数字式ZVS移相全桥电动汽车充电器[D].天津：天津大学，2012.

[7]     张涛，刘胜道，祝小雨. 移相全桥变换器电压模式控制器的设计与仿真[J].船电技术，2013，33（10）：28-30.

[8]     余帅，刘胜永，崔志鹏，等. 基于V2G充电桩系统DC-DC变换器控制策略的研究[J].广西科技大学学报，2018，29（1）：69-75.

[9]     赵华高. 移相全桥ZVS变换器的研究[D].杭州：浙江工业大学，2010.

[10]   樊俊峰. 新型分布式直流电源系统[D].南京：河海大学，2003.

[11]   李艳.软开关双输入全桥变换器的参数设计[J].电工技术学报，2011，26（9）：167-174，189.

[12]   苏敏，邹旭东.基于SiC MOSFET的移相全桥ZVS变换器[J].电源学报，2018，16（3）：36-43.

[13]   张斌，张彦会，史维玮，等. 基于纯电动汽车的双输入双向DC/DC变换器设计[J].广西科技大学学报，2014，25（4）：67-71.

[14]   段宣祥，贺明智，张立伟. 移相全桥变换器占空比丢失问题的研宄[J].电力电子技术，2012，46（4）：26-28.

Abstract： In view of the fact that the phase-shifted full-bridge converter gradually decreases with load， the switch of the lagging arm realizes the narrowing of the soft-switching range and the converter efficiency is reduced. The condition of the soft-switching of the bridge arm is to study the influence of different values of the resonant inductor on the duty cycle loss， the soft-switching of the lagging arm， and the converter efficiency by analyzing the working principle of the converter and realize soft switching condition about the bridge arm of the converter. The phase-shifted full-bridge converter circuit parameters are designed and simulated by saber software. The results verify the appropriate resonant inductor value， which can increase the soft-switching range of the lagging arm and optimize the converter efficiency.

Key words： phase shift full bridge converter; soft switch; efficiency optimization; lagging leg; resonance inductor

（責任编辑：黎   娅）