基于UKF方法的锂离子电池荷电状态估计研究

李泽洋 李振强 吕丰

摘    要：选用二阶RC回路的电池模型，以单体的磷酸铁锂动力电池为研究对象，通过充电/放电电流脉冲实验获得电池模型中的各个参数变化范围，研究其荷电状态（SOC）的估算方法.根据电池模型的状态方程和输出方程，运用MATLAB软件，利用无迹卡尔曼滤波（UKF）方法来估算锂离子电池的SOC，并将其估算结果与扩展卡尔曼滤波（EKF）方法的估算结果进行比较.实验结果表明UKF方法能够更精确地估计出动力电池的SOC.

关键词：锂离子电池;无迹卡尔曼滤波;扩展卡尔曼滤波;SOC估计

中图分类号：TM912        DOI：10.16375/j.cnki.cn45-1395/t.2019.03.007

引言

电池的荷电状态（SOC）[1]通常为衡量电池剩余容量的重要指标，由于无法直接通过仪表测量，只能利用测量的电池工作电压、电流等外部特性参数，选用适当的估计算法进行估算.因此，准确估算动力电池的SOC在电动汽车应用方面是研究的重点.

目前有许多种研究电池SOC的估计方法.安时法[2]为一种常见的估算方法，当电流恒定时，利用安时法能够准确估计出动力电池的SOC;当电流波动较大时，由于存在误差累积效应，估算电池SOC的准确度降低.开路电压法[3]是利用测量电池的开路电压来估计电池的SOC，但是该方法不能在线估计动态电池的SOC.神经网络法[4]具有较好的自学习能力，但是受到训练方法和培训数据的影响，估计电池SOC的误差较大.卡尔曼滤波（KF）方法[5]能够对线性系统进行建模，常用于估计模型的参数，但是，锂离子电池由于充/放电的原因，电池内部有极化效应和扩散效应，电池的动态模型为时变的非线性系统.EKF方法[6-7]能够估计动力电池的SOC，要对非线性系统进行线性化，只能保留其一阶导数项与常数项，忽略非线性函数的高阶导数项，因此，估计电池的SOC有很大的误差.UKF方法[8-9]是利用无迹变换（UT）[10]来处理数据，扩展数据长度，将原数据加权重构，保持数据的均值与方差不变，运用扩展的数据对非线性系统的参数进行估计，参数估计的误差与EKF方法相比较小.本文创新之处在于应用实测的动力电池的充/放电数据，建立其数学模型，针对此模型中时变参数，通过大量实验，获得了时变参数的变化范围，再运用UKF方法估算出动力电池的SOC，估计的SOC更加准确.

1    动力电池建模及参数估算

在动力电池的特性研究中，精确的电池模型有助于准确地描述电池的内部特性.等效电路模型[11]可以通过改变输入电流信号来模拟锂离子电池的不同工作状况，并可以有效地模拟电池的动态特性，广泛应用于锂离子电池建模.等效电路模型不仅能与其他方法互相结合，而且计算简便，使模型更准确.因为动力电池具有强非线性特点，选用多阶RC等效电路模型，得到的准确度会更高.但是，当RC回路的数量增加时，电池模型复杂程度和数据计算量也会随之增加.为了便于工程应用，本文选用同一批次的多块单节天津力神第二代磷酸铁锂动力电池（3.2 V/20 Ah）作為研究对象，选用二阶RC回路的电池模型，如图1所示.

图1中，UOC是开路电压，其随SOC的变化而变化;U为锂离子电池的端电压;I是放电电流，取动力电池放电时电流方向为等效电路模型的正方向;R0为欧姆内阻;动力电池在充放电过程中，电池内部存在极化效应和扩散效应，用R1、C1表示电池内部极化效应，R2、C2则表示扩散效应.

2    卡尔曼滤波法估计SOC

将电池模型设为非线性系统，并使用非线性函数描述为：

式中，[f（⋅）]和[g（⋅）]分别为系统的状态函数和观测函数;x（k）为系统的n维状态变量;u（k）为系统输入变量;W（k）是n维系统过程噪声，其均值为零列向量[01×n]，方差矩阵为[Qn×n];[V（k）]为[m]维系统观测噪声，其均值为零列向量[01×m]，方差矩阵为[Rm×m].下面分别介绍EKF方法和UKF方法估计SOC.

2.1   EKF方法估计SOC

EKF方法是基于线性KF的方法之上，将非线性函数[f（⋅）]和[g（⋅）]展开成泰勒级数并略去二阶以上项，获得近似线性模型，然后使用KF完成目标的估计.具体步骤如下：

3    实验仿真

通过大量的充放电实验，确定电池的初始容量为16 Ah，用0.5 C（10 A）的电流对电池进行了连续放电实验，测量得到电池的端电压和放电消耗的电池容量（安时值）.利用MATLAB仿真工具，基于UKF方法和标准EKF方法对锂离子电池SOC进行估算，估算结果与实际测量的电池容量进行比较，判断两种估算方法的有效性.

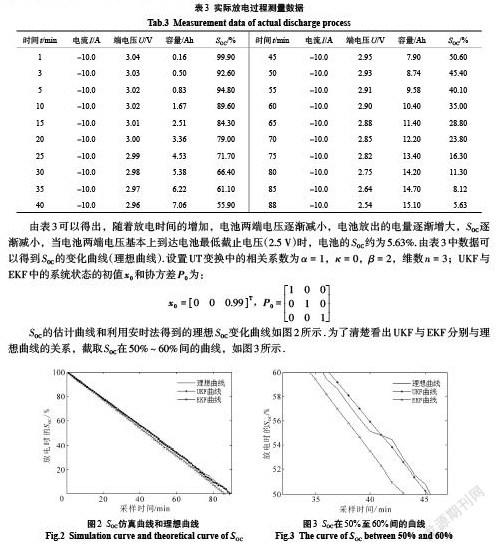
通过实验室中的电池测试系统对电池进行放电实验，每1 min采集一次数据.由于篇幅要求，将实验数据进行简化，得到实际测量数据如表3所示.

由表3可以得出，随着放电时间的增加，电池两端电压逐渐减小，电池放出的电量逐渐增大，SOC逐渐减小，当电池两端电压基本上到达电池最低截止电压（2.5 V）时，电池的SOC约为5.63%.由表3中数据可以得到SOC的变化曲线（理想曲线）.设置UT变换中的相关系数为[α=1]，[κ=0]，[β=2]，维数[n=3];UKF与EKF中的系统状态的初值[x0]和协方差[P0]为：

SOC的估计曲线和利用安时法得到的理想SOC变化曲线如图2所示.为了清楚看出UKF与EKF分别与理想曲线的关系，截取SOC在50%～60%间的曲线，如图3所示.

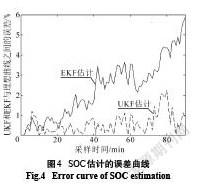
从图2和图3中可以看出，由于标准EKF将非线性方程进行线性化处理，与理想SOC曲线之间的误差较大;而UKF不对非线性方程在估计点处做线性化处理，估计SOC更加接近于理想的SOC曲线，在估计过程中的收敛性更好.图4是利用标准EKF方法与UKF方法预估SOC的误差比较曲线.

从图4中可以看出，标准EKF的估计误差逐渐增大，最大估计误差达到6%，而UKF估计SOC的误差变化比较平缓，最大误差在2%.由此可知，UKF估计SOC的精度高于标准EKF的估计精度.所以，对于锂离子电池这种强非线性系统，UKF相对于标准EKF而言，在估计过程中避免了由于线性化过程忽略高阶项带来的误差，具有更高的预估精度，更适用于预估动力电池SOC的研究.

4    结论

通过对磷酸铁锂动力电池进行大量的充放电实验，获得了大量测量数据;利用MATLAB软件将这些数据进行曲线拟合，得到电池模型中各个参数后建立电池模型的状态方程和观测方程，分别利用UKF与EKF方法对电池的SOC进行预估.因为EKF方法对非线性函数进行泰勒级数展开并保留二阶以下的项，所以由于函数的线性化造成较大误差;而利用UKF方法来估计SOC，通过分布式采样的UT变换来计算非线性系统的统计特性，避免了由于线性化带来的误差.通过大量仿真实验，验证了UKF预估SOC的精确度高于标准EKF估计的精确度.

参考文献

[1]     左红明，张彦会，陆文祺，等. 移动充电系统的锂电池SOC的估算及检测设计[J]. 广西科技大学学报，2019，30（1）：71-78.

[2]     ZHANG Y H，SONG W J，LIN S L，et al. A novel model of the initial state of charge estimation for LiFePO4 batteries[J]. Journal of Power Sources，2014，248：1028-1033.

[3]     XU L，WANG J P，CHEN Q S. Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model[J]. Energy Conversion and Management，2012，53（1）：33-39.

[4]     HU X S，SUN F C，ZOU Y. Comparison between two model-based algorithms for Li-ion battery SOC estimation in electric vehicles[J]. Simulation Modelling Practice and Theory，2013，34：1-11.

[5]     黄世回，蔡启仲，王汝钢. 储能电站蓄电池SOC在线最优估计[J]. 广西工学院学报，2013，24（2）：40-45.

[6]     RAMADAN H S，BECHERIF M，CLAUDE F.  Extended kalman filter for accurate state of charge estimation of lithium-based batteries：a comparative analysis[J]. International Journal of Hydrogen Energy，2017，290：33-46.

[7]     陈峭岩. 电动汽车电池状态估计及均衡管理研究[D]. 天津：天津大学，2014.

[8]     HE W，WILLIARD N，CHEN C C，et al. State of charge estimation for electric vehicle batteries using unscented kalman filtering[J]. Microelectronics Reliability，2013，53（6）：840-847.

[9]     CHEN Z W，YANG L W，ZHAO X B，et al. Online state of charge estimation of Li-ion battery based on an improved unscented kalman filter approach[J]. Applied Mathematical Modelling，2019，70：532-544.

[10]   DONG G Z，WEI J W，CHEN Z H，et al. Remaining dischargeable time prediction for lithium-ion batteries using unscented kalman filter[J]. Journal of Power Sources，2017，364：316-327.

[11]   張彦会，李鑫，左红明. 磷酸铁锂电池滞回特性的修正算法研究[J]. 广西科技大学学报，2018，29（1）：31-36.

[12]   李振强，邹丽蓉，黄杰. 锂电池的模型参数与荷电状态估计的研究[J]. 通信电源技术，2016，33（1）：18-21.

[13]   GREWAL M S，ANDREWS A P. 卡尔曼滤波理论与实践（MATLAB版）[M].4版. 刘郁林，陈绍荣，徐舜，译. 北京：电子工业出版社，2017.

[14]   KANDEPU R，FOSS B，IMSLAND L. Applying the unscented kalman filter for nonlinear state estimation[J]. Journal of Process Control，2008，18（7-8）：753-768.

Abstract： The estimation method of the state of charge （SOC） of single lithium-ion phosphate power battery is studied. The battery model is given by the second-order RC equivalent circuit， and the range of the parameters of the equivalent circuit model is obtained by the charging/discharging current pulse experiment. According to the state equation of the battery model， the unscented Kalman filter （UKF） method is used to estimate the SOC of lithium-ion batteries by using MATLAB software. The results of SOC estimation are compared with that of the extended Kalman filter （EKF） method. The experimental results show that UKF method can estimate the SOC of lithium-ion batteries more accurately.

Key words： lithium-ion battery; unscented Kalman filter; extended Kalman filter; SOC estimation

（责任编辑：黎  娅）