基于Copula函数的郑州市外调水供水补偿特性
2019-09-10张倩吴泽宁吕翠美郭溪高申
张倩 吴泽宁 吕翠美 郭溪 高申





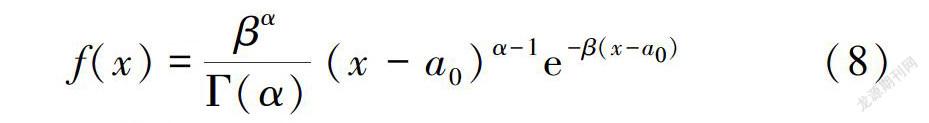
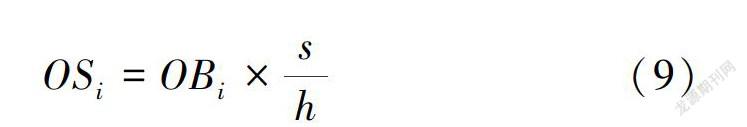


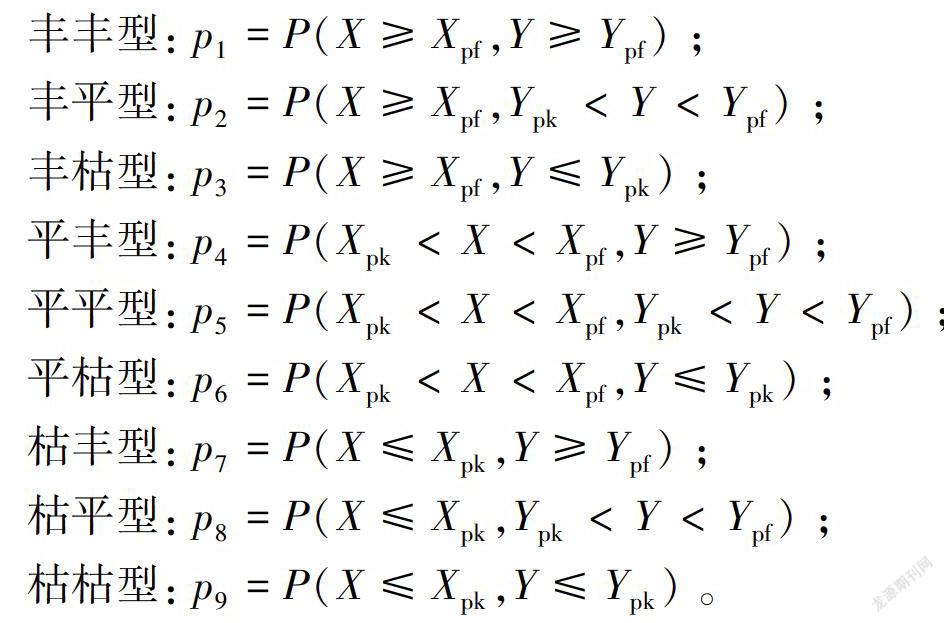


摘要:南水北调工程供水和黄河供水是郑州市城区的两个主要外调水源,对两者的相互补偿特性及其对郑州市城区供水的补偿特性进行分析,可为制定郑州市城区供水方案、提高供水保证率提供参考。在发现南水北调工程供水也具有一定的频率特性的背景下,以两者的供水频率分析为基础,使用优选的Copula函数,对郑州市城区南水北调工程供水和黄河供水进行补偿特性计算分析,结果表明:①在丰枯同步组合类型中,两种水源同枯的频率最大,同平的频率最小,发生同枯的风险较大,易造成供水短缺风险,此时应积极调配水源;②同丰时水量充足,可利用调蓄水库将多余水量存蓄,供枯时使用;③在丰枯异步组合类型中,丰与枯组合的频率最大,枯与平组合的频率最小;④丰枯异步的频率大于丰枯同步的频率,说明两水源互补性较好。
关键词:南水北调工程;补偿特性;Copula函数;供水量;频率分析;郑州市
中图分类号:TV213.4
文献标志码:A
doi:10.3969/j.issn.1000- 1379.2019. 04.009
随着城市化进程加快,亟需更高的供水保证率来保障社会运转。提高城市供水保证率的有效途径之一是对供水进行合理高效利用。水厂调度往往涉及多个水源,不同的多水源供水频率组合会产生不同的可供水量结果,取多年平均或某一频率的供水量无法为实际的水资源调度提供准确支持,在一定程度上降低了对水资源的利用率。对不同供水进行补偿特性分析有助于解决这一问题。陈守煜等[1]采用方差分析和模糊假设检验对碧流河水库汛期和非汛期来水的补偿特性进行了分析,姜彪等[2]对碧流河水库及英那河水库的来水进行了补偿分析,王妍等[3]运用Copula函数对大伙房水库输水工程的水源区和受水区的径流丰枯补偿特性进行了研究。
南水北调中线工程和黄河供水工程是向郑州市城区供水的主要工程,对保障城区的用水起着重要作用。受水源地水资源条件变化、不同时节沿途蒸发及水权交易等因素的影响[4],南水北调中线工程对郑州市城区的供水存在年际差异,和黄河一样丰枯情况年年不同,两者可供水量的丰枯组合情况也不同。目前对两者供水的补偿特性分析研究较少。本文通过优选的Copula函数,对郑州市城区的南水北调工程供水和黄河供水的补偿特性进行分析,得到9种丰枯组合中两种水源的丰枯同步、异步频率,以期为水资源调度提供参考。
1 研究区概况与数据选取
2016年年底郑州市成为国家中心城市,亟需良好的城市供水能力以保障经济发展。郑州市城区是郑州市的核心发展区域,近年来水资源面临诸多问题:①用水量激增.2017年总用水量比2007年增加了123.5%:②水资源量呈减少趋势.2017年水资源总量比2007年减少了35.9%:③尖岗水库和常庄水库是郑州市城区的重要备用水源,但近年来水库来水量锐减,致使城区应对突发情况能力弱[5]。现阶段主要外调水源黄河水和南水北调工程供水的丰枯情况不同,对两者的补偿特性进行分析可为解决上述问题提供帮助。
鉴于南水北调工程实际供水的时间序列较短,而《南水北调中线一期工程可行性研究总报告(2005)》的研究时段为1956-1997年,本文使用1956-1997年南水北调工程对河南省的规划供水数据,对其进行处理后得到对郑州市城区的供水数据。黄河对郑州市城区的供水量序列按照“丰增枯减”的分水原则,对1956-1997年的黄河花园口水文站的来水数据进行处理后得到。
2 基于Copula函数的不同供水补偿特性分析方法
Copula函数是构建联合分布的一种有效方法,它的优势在于能够灵活地构造边缘分布为任意分布的水文变量联合分布,边缘分布和相关性结构可以分开考虑,对正负相关性都适用[6]。
2.1 分布函数的确定
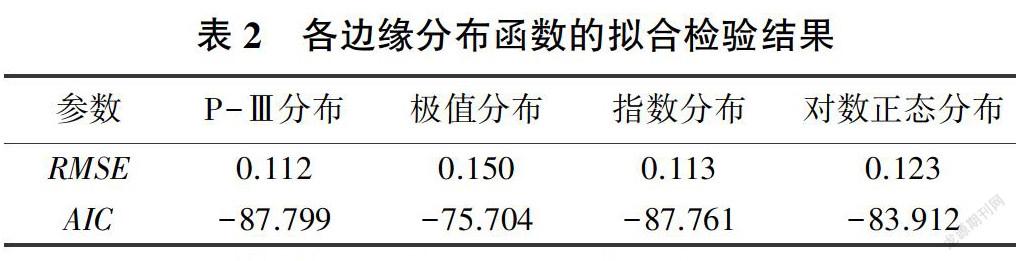
P-Ⅲ型分布函数广泛适用于我国水文频率的计算[7]。对于非天然河流,分别用P-Ⅲ型分布、极值分布、指数分布和对数正态分布对数据进行拟合,采用均方根误差法(RMSE)和AIC信息准则法选定最优分布函数:
3 结果与讨论
3.1 供水频率分析
3.1.1 南水北調工程供水频率分析
根据1956-1997年南水北调工程对河南省的规划供水量,按下式折算可得到对郑州市城区的可供水量:
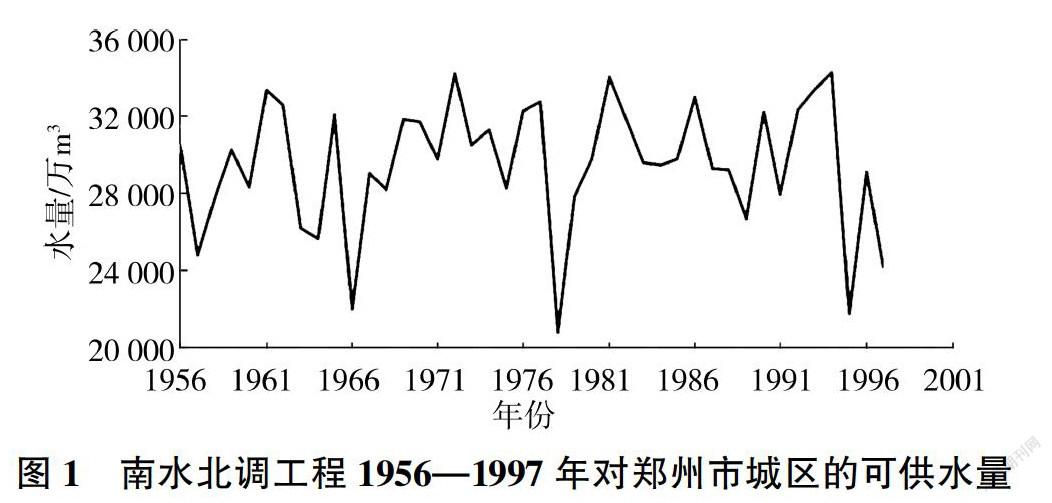
由式(7)得到的南水北调工程1956-1997年对郑州市城区的供水量见图1。由图1可知,南水北调工程对郑州市城区的最大年可供水量为34 305万m,最小年可供水量为20 734万m,多年平均可供水量为29 521万m,表明南水北调工程供水具有年际变化不均的特点。
将南水北调工程对郑州市城区的多年可供水量代人各分布函数,对其拟合性进行检验,由式(1)、式(2)得到RMSE值和AIC值,见表2。可以看出,P-Ⅲ型分布AIC值最小,拟合程度最好。
黄河对郑州市城区1956-1997年的可供水量见图2。由图2可知,黄河年可供水量最大值为5 131万m3,最小值为852万m,表明黄河水供水具有年际不均的特点。对黄河水供水序列的边缘分布函数的参数进行估计,得到x =2 416万m3、Cv =0.365 1.Cs=0.867 3,由式(8)可得到最优边缘分布函数表达式。
3.2 补偿特性频率分析
3.2.1 Copula函数优选
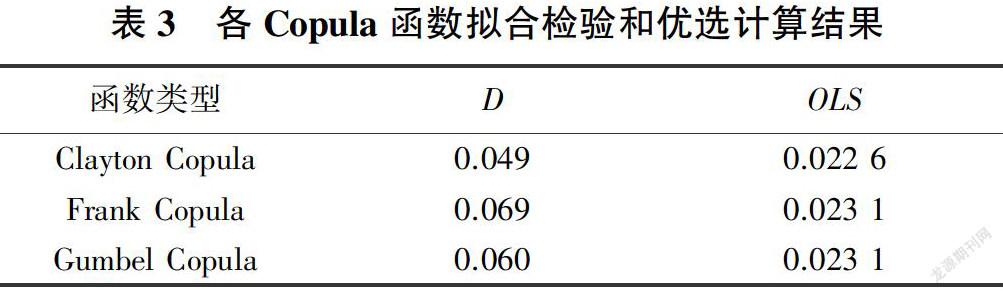
对各Copula函数进行拟合检验,由式(4)、式(5)得到检验统计量D和离差平方和O/S的值(见表3)。显著性水平a= 0.05、n=42对应的D(n,a)= 0.210,各函数的D值都小于0.210,通过了K-S检验。其中Clayton Copula函数的O/S值最小,可作为最优联合函数。利用Clayton Copula函数计算理论频率,将其与经验频率拟合(见图3),可以看出拟合程度较好。
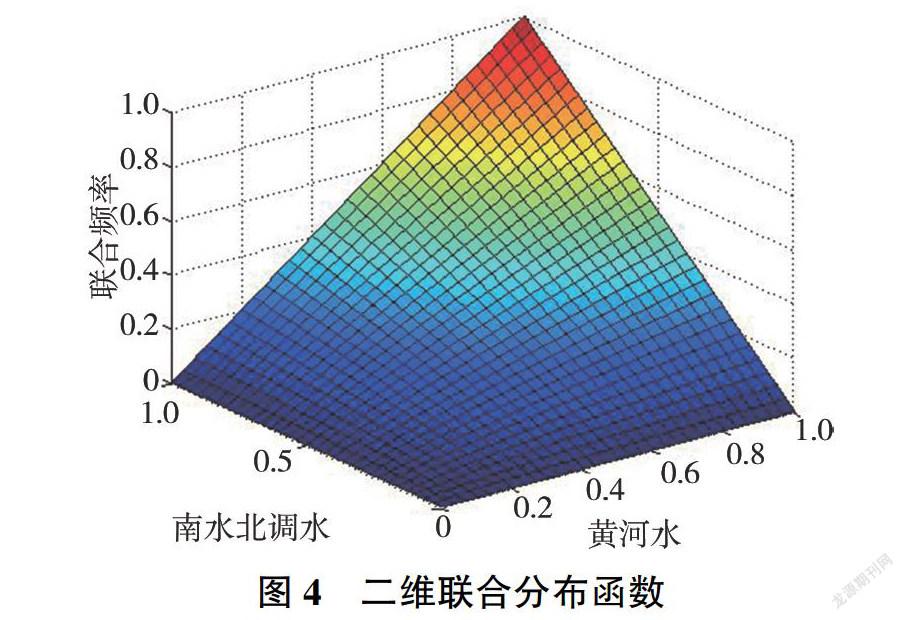
通过南水北调工程供水和黄河供水的边缘分布函数拟合出最优联合分布函数,得到二维联合分布函数图(见图4).据此可得出郑州市城区两水源来水分别对应不同丰枯情况时的联合频率,还可以得出此联合频率对应的南水北调工程和黄河供水量。对郑州市城区两水源各自丰枯情况下对应的来水量进行计算,结果见表4。
对南水北调工程供水X和黄河供水y不同丰枯情况进行组合,可以得到以下9种类型。
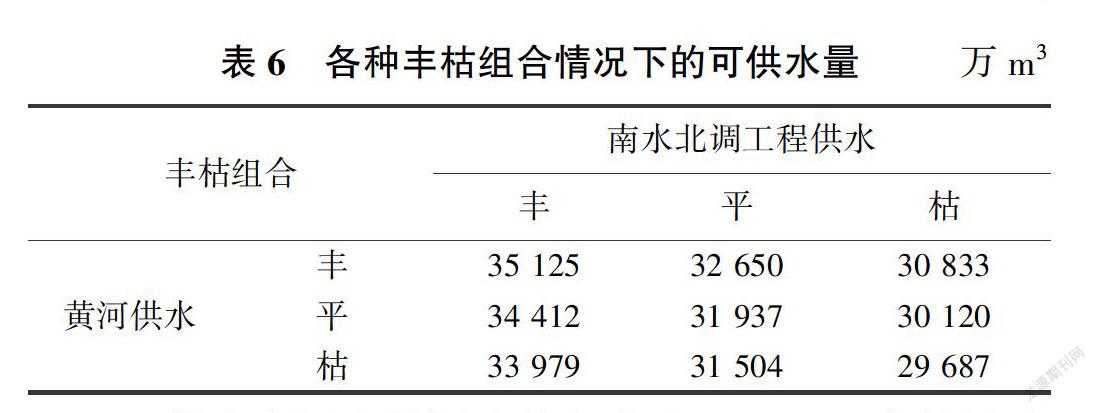
其中:丰丰型、平平型和枯枯型为丰枯同步,其他为丰枯异步。运用优选出的Clayton Copula函数对9种丰枯组合的频率分别进行计算,结果见表5.对应的可供水量见表6。
两供水水源丰枯同步的频率为37.66%,丰枯异步的频率为62.34%,丰枯异步频率大于丰枯同步频率24.68%。9种丰枯组合类型中,枯枯型的频率最大(为15.99%),丰丰型的次之(为15.32%),丰丰型频率仅比枯枯型频率小0.67%,平平型的频率最小(为6.35%)。两水源同丰时可供水量最大,为35 125万m3,同枯时可供水量最小,为29 687万m,两种情况可供水量相差5 438万m3,两水源同枯时可供水量有极大可能不足。丰平型和平丰型的频率都为9. 66%.但丰平型的可供水量为34 412万m,平丰型的可供水量为32 650万m3,丰平型比平丰型的可供水量多1 762万m。丰枯型和枯丰型的频率都为12.52%,但丰枯型的可供水量为33 979万m.枯丰型的可供水量为30 833万m.丰枯型比枯丰型的可供水量多3 146万m。平枯型和枯平型的频率都为8.99%,但平枯型的可供水量为31 504万m.枯平型的可供水量为30 120万m3,平枯型比枯平型的可供水量多1 384万m。丰与枯组合的频率为25.04%,丰与平组合的频率为19.32%,平与枯组合的频率为19.98%。
综上分析,南水北调工程供水和黄河供水同枯的风险最大,易造成供水短缺风险,此时两外调水源必须和调蓄水库联合调度,才能保障社会生活的正常用水。同丰时,供水量充足,可以将多余水量通过水库蓄起来,在供水短缺时使用。丰与枯组合加起来的频率最大、平与枯组合加起来的频率次之,该情况下两水源供水能够互补,可以降低供水短缺风险。
4 结语
(1)郑州市城区南水北调工程供水和黄河供水丰枯异步频率大于丰枯同步频率,说明南水北调工程供水和黄河供水的互补性较好。丰枯异步中,丰与枯、平与枯组合的情况下两水源供水能够互补。郑州市城区的南水北调工程供水和黄河供水丰与枯组合加起来的频率最大,联合供水可以有效降低一方枯水时的供水短缺风险。
(2)9种丰枯组合中,水源同枯的频率最大、可供水量最小,对供水最不利,说明两水源联合供水发生供水短缺的风险较大。
(3)水源同丰频率仅较同枯低0.67%,此时两水源的可供水量为35 125万m.对供水最有利,水源同枯可供水量为29 687万m.两者相差5 438万m,可联合调蓄水库将同丰时多余水量存储起来,以供同枯时使用。
本文所用的供水资料是根据规划资料得到,且时间较早,随着人类活动和气候变化的影响,未来的来水径流可能会发生变化,因此未来来水条件下的丰枯遭遇情况还需进一步研究。本文的研究对象是郑州市城区,没有涵盖到整个市区,且只研究了外调水源,更大范围的不同水源联合调度也有待进一步研究。
参考文献:
[1]陈守煜,赵瑛琪,许士国,跨流域径流补偿特性与提高供水能力的研究[J].水利学报,1988(3):37-41.
[2]姜彪,孙万光,邓显羽,等,跨流域联合供水水库补偿特性研究[J].水文,2016,36(5):33-38.
[3]王妍,王强,基于Copula函数的输水工程径流丰枯补偿特性研究[J].东北水利水电,2018,36(7):37-39.
[4]陈璐.Copula函数理论在多变量水文分析计算中的应用研究[M].武漢:武汉大学出版社,2013:28.
[5]水利部,水利水电工程水文计算规范:SL 278-2002[S].北京:中国水利水电出版社,2002:14.
[6] 冯平,牛军宜,张永,等,南水北调西线工程水源区河流与黄河的丰枯遭遇分析[J].水利学报,2010,41(8):900-907.
[7]ZHANC L Multivariate Hydrological Frequency Analysis andRisk Mapping[ D]. Baton Rouge: Louisiana State University,2005:42-43.
[8] 郑红星,刘昌明,南水北调东中两线不同水文区降水丰枯遭遇性分析[J].地理学报,2000,55(5):523-532.
[9] 高申,郑州市城区跨流域调水工程与调蓄水库联合调度研究[D].郑州:郑州大学,2017:13-16.
[10] 曹燕燕,干旱时空变化及分布特征研究[D].天津:天津大学,2012:29-33.
[11] 戴昌军,多维联合分布计算理论在南水北调东线丰枯遭遇分析中的应用研究[D].南京:河海大学,2005:73-76.
[12] 鞠兵,吴克宁,李玲,等,河南省典型土系的特定土层特征与分类研究[J].土壤学报,2016,53(1):48-57.
[13] 何小聪,基于贝叶斯网络的跨流域调水工程水文风险分析研究[D].武汉:华中科技大学,2012:34-35.
[14] 曹根堂,基于水利水电勘测设计信息管理的计算机集成应用系统探究[J].电子测试,2015(4):100-102.
[15] 鲁克江,灌区季节性水价的确定及实施[J].中国农村水利水电,2000(10):9-10.
